中南大学自动化学院“智能控制与优化决策”课题组-第七章贝叶斯分类器任务小结
1. 解释先验概率、后验概率、全概率公式、条件概率公式,结合实例说明贝叶斯公式,如何理解贝叶斯定理?
- 先验概率
先验概率 P ( c ) P(c) P(c)表达了样本空间各类样本所占的比例,根据大数定律,当训练集包含充足的独立分布的样本时, P ( c ) P(c) P(c)可通过各类样本出现的频率来进行估计。 - 后验概率
后延概率 P ( c ∣ x ) P(c|x) P(c∣x),可以理解为在类别 c c c在训练集 x x x下所谓的“真实出现的概率” - 全概率公式
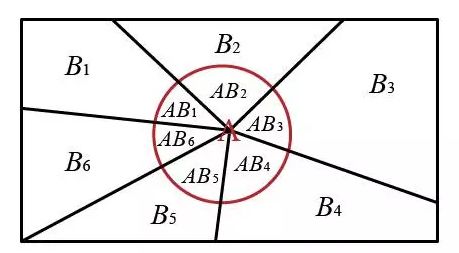
如图所示,一个样本空间 S S S 被 B 1 , B 2 . . . B 6 B_1,B_2...B_6 B1,B2...B6 这样一个完备事件组完美瓜分,红色圆圈内标有的事件 A A A 也被无情的分解到各部分去, 现在我们这支离破碎的事件 A A A 拼凑起来:
P ( A ) = P ( A B 1 ) + P ( A B 2 ) + . . . + P ( A B 6 ) = P ( A ∣ B 1 ) P ( B 1 ) + P ( A ∣ B 2 ) P ( B 2 ) + . . . P ( A ∣ B 6 ) P ( B 6 ) P(A)=P(AB_1)+P(AB_2)+...+P(AB_6)\\=P(A|B_1)P(B_1)+P(A|B_2)P(B_2)+...P(A|B_6)P(B_6) P(A)=P(AB1)+P(AB2)+...+P(AB6)=P(A∣B1)P(B1)+P(A∣B2)P(B2)+...P(A∣B6)P(B6) - 条件概率公式
P ( A ∣ B ) P(A|B) P(A∣B) 表示在事件 B B B 发生的条件下,事件 A A A 发生的概率 - 贝叶斯公式
P ( B i ∣ A ) = P ( B i A ) P ( A ) = P ( A ∣ B i ) P ( B i ) ∑ j = 1 n P ( A ∣ B j ) P ( B j ) P(B_i|A)=\frac{P(B_iA)}{P(A)}=\frac{P(A|B_i)P(B_i)}{\sum_{j=1}^{n}P(A|B_j)P(B_j)} P(Bi∣A)=P(A)P(BiA)=∑j=1nP(A∣Bj)P(Bj)P(A∣Bi)P(Bi)
简单的来说,贝叶斯定理是基于假设的先验概率、给定假设下观察到不同数据的概率,提供了一种计算后验概率的方法。
2. 结合实例说明朴素贝叶斯分类器是如何对测试样本进行分类的?并归纳总结算法步骤。
朴素贝叶斯是贝叶斯证据独立的表达形式,属于一种特例。实际应用过程中贝叶斯表达式非常复杂,但是我们希望把它拆分成多个朴素贝叶斯来表达,这样能够快速获得后验概率。
朴素贝叶斯的基本思想:对于给定的待分类项 x x x{ x 1 , x 2 , . . . x n x1,x2,...xn x1,x2,...xn} ,求解在此项中出现的条件下各类别 c i c_i ci 出现的概率。哪个 P ( c i ∣ x ) P(c_i|x) P(ci∣x) 最大,就把此待分类项归属于哪个类别。
算法步骤:
-
1
每个数据样本用一个n维特征向量 x = x= x= { x 1 , x 2 , . . . x n x1,x2,...xn x1,x2,...xn}表示,分别描述对n个属性 A 1 , A 2 , . . . A n A1,A2,...An A1,A2,...An 样本的 n 个度量. -
2
假设有 m 个类 c 1 , c 2 , . . . , c m c_1,c_2,...,c_m c1,c2,...,cm , 给定一个未知的数据样本 x x x, 分类器将预测 x x x 属于具有最高后验概率的类。也就是说,朴素贝叶斯分类将未知的样本分配给类 c i ( 1 ⩽ i ⩽ m ) c_i (1\leqslant i \leqslant m ) ci(1⩽i⩽m) 当且仅当 P ( c i ∣ x ) > P ( c j ∣ x ) i ≠ j P(c_i|x)>P(c_j|x) \ \ i \neq j P(ci∣x)>P(cj∣x) i=j . 这样,最大化 P ( c i ∣ x ) P(c_i|x) P(ci∣x). 其 P ( c i ∣ x ) P(c_i|x) P(ci∣x) 最大的类 c i c_i ci 称为最大后验假定。根据贝叶斯定理:
P ( c i ∣ x ) = P ( x ∣ c i ) P ( c i ) P ( x ) P(c_i|x)=\frac{P(x|c_i)P(c_i)}{P(x)} P(ci∣x)=P(x)P(x∣ci)P(ci) -
3
由于 P ( x ) P(x) P(x) 对于所有类为常数,只需要 P ( x ∣ c i ) P ( c i ) {P(x|c_i)P(c_i)} P(x∣ci)P(ci) 最大即可. 如果 c i c_i ci 类的先验概率未知,则通常假定这些类是等概率的,即 P ( c 1 ) = P ( c 2 ) = . . . = P ( c m ) P(c_1)=P(c_2)=...=P(c_m) P(c1)=P(c2)=...=P(cm) , 因此就转化为对 P ( x ∣ c i ) P(x|c_i) P(x∣ci) 的最大化( P ( x ∣ c i ) P(x|c_i) P(x∣ci)常被称为给定 c i c_i ci 时数据 x x x 的似然度,而使 P ( x ∣ c i ) P(x|c_i) P(x∣ci) 最大的假设 c i c_i ci 称为最大似然度. 否则,需要最大化 P ( x ∣ c i ) P ( c i ) {P(x|c_i)P(c_i)} P(x∣ci)P(ci). 注意,类的先验概率可以用 P ( c i ) = s i / s P(c_i)=s_i / s P(ci)=si/s 计算,其中 s i s_i si 是 c i c_i ci 中的训练样本数, s s s是训练样本总数. -
4
给定具有许多属性的数据集,计算 P ( x ∣ c i ) P(x|c_i) P(x∣ci) 的开销可能非常大. 为降低计算 P ( x ∣ c i ) P(x|c_i) P(x∣ci) 的开销, 可以做类条件独立的朴素假定. 给定样本的类标号,假定属性值相互条件独立,即在属性间,不存在依赖关系. 这样只需考虑分子:
P ( x ∣ c i ) = ∏ k = 1 n P ( x k ∣ c i ) P(x|c_i)=\prod_{k=1}^{n}P(x_k|c_i) P(x∣ci)=k=1∏nP(xk∣ci) -
5
对未知样本 x x x 分类, 也就是对每个类 c i c_i ci,计算 P ( x ∣ c i ) P ( c i ) {P(x|c_i)P(c_i)} P(x∣ci)P(ci) ,朴素贝叶斯分类将未知的样本分配给类 c i ( 1 ⩽ i ⩽ m ) c_i (1\leqslant i \leqslant m ) ci(1⩽i⩽m) 当且仅当 P ( c i ∣ x ) > P ( c j ∣ x ) i ≠ j P(c_i|x)>P(c_j|x) \ \ i \neq j P(ci∣x)>P(cj∣x) i=j . 这样, x x x 被指派到其 P ( x ∣ c i ) P ( c i ) {P(x|c_i)P(c_i)} P(x∣ci)P(ci) 最大的类.
流程图如下图所示:
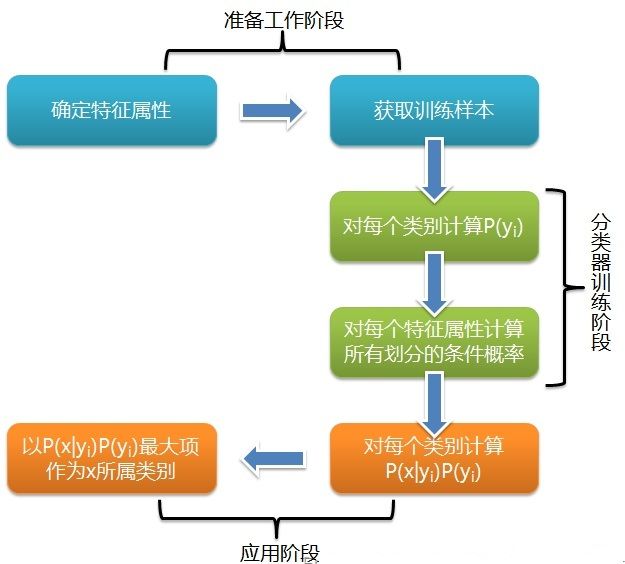
-
实例分析
有一批同一型号的产品,已知其中由一厂生产的占15%,二厂生产的占80%,三厂生产的占5%,又已知这三个厂的次品率分别为2%,1%,3%. 从这批产品中任取一件是次品,问这件次品属于哪家工厂的概率最大:
设 A A A 表示“取到的是一只次品”, B i B_i Bi表示“所取到的次品是由第i家工厂提供的”,则 B 1 , B 2 , B 3 B_1,B_2,B_3 B1,B2,B3 是样本空间的 Ω \Omega Ω 的一个划分,且 P ( B 1 ) = 0.5 , P ( B 2 ) = 0.80 , P ( B 3 = 0.05 ) P(B_1)=0.5,P(B_2)=0.80,P(B_3=0.05) P(B1)=0.5,P(B2)=0.80,P(B3=0.05)

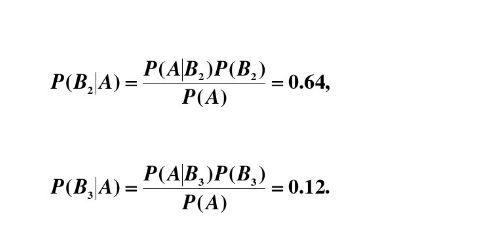
由此可见,来自工厂二的概率最大。
3. 分别说明如何用极大似然估计和贝叶斯估计进行朴素贝叶斯的参数估计。
-
极大似然估计
极大似然估计要估计的参数 θ \theta θ 被当作是固定形式的一个未知变量,然后我们结合真实数据通过最大化似然函数来求解这个固定形式的位置变量. 具体求解过程如下: -
假设样本集 D = D= D= { x 1 , x 2 , . . . x n x_1,x_2,...x_n x1,x2,...xn}, 假设样本之间都是相对独立的,于是便有:
P ( D ∣ θ ) = P ( x 1 ∣ θ ) P ( x 2 ∣ θ ) . . . P ( x n ∣ θ ) P(D|\theta)=P(x_1|\theta)P(x_2|\theta)...P(x_n|\theta) P(D∣θ)=P(x1∣θ)P(x2∣θ)...P(xn∣θ)
所以假设似然函数为:
L ( θ ∣ D ) = ∏ k = 1 n P ( x k ∣ θ ) L(\theta|D)=\prod_{k=1}^{n}P(x_k|\theta) L(θ∣D)=k=1∏nP(xk∣θ)
接下来我们求参的准则便是如同名字一样最大化似然函数:
θ = a r g max θ L ( θ ∣ D ) \theta =arg \max_\theta L(\theta|D) θ=argθmaxL(θ∣D) -
贝叶斯估计
贝叶斯估计则是将参数视为是有某种已知先验分布的随机变量,意思便是这个参数不是一个固定的未知数,而是符合一定先验分布如:随机变量 θ \theta θ 符合正态分布等.
-贝叶斯估计最终也是为了得出后验概率,它最终要推导的是:
P ( w i ∣ x , D ) = P ( w i ∣ x , D ) P ( x , D ) = P ( w i , x , D ) ∑ j = 1 c P ( w i , x , D ) P(w_i|x,D)=\frac{P(w_i|x,D)}{P(x,D)}=\frac{P(w_i,x,D)}{\sum_{j=1}^{c} P(w_i,x,D)} P(wi∣x,D)=P(x,D)P(wi∣x,D)=∑j=1cP(wi,x,D)P(wi,x,D)
上式中有:
P ( w i , x , D ) = P ( x ∣ w i , D ) P ( w i ) ∑ j = 1 c P ( w i , x , D ) P(w_i,x,D)=\frac{P(x|w_i,D)P(w_i)}{\sum_{j=1}^{c} P(w_i,x,D)} P(wi,x,D)=∑j=1cP(wi,x,D)P(x∣wi,D)P(wi)
这里也有一个重要的假设,那就是样本之间是相互独立的,同时类也是独立的,所以有如下假设:
P ( w i ∣ D ) = P ( w i ) P ( x ∣ w i , D ) = P ( x ∣ w i , D i ) P(w_i|D)=P(w_i) \\ P(x|w_i,D)=P(x|w_i,D_i) P(wi∣D)=P(wi)P(x∣wi,D)=P(x∣wi,Di)
同时由于类与类之间相互独立,便有:
P ( x ∣ w i , D i ) = P ( x ∣ D ) P(x|w_i,D_i)= P(x|D) P(x∣wi,Di)=P(x∣D)
类似于极大似然函数的推导,可得:
P ( D ∣ θ ) = ∏ k = 1 n P ( x k ∣ θ ) P(D|\theta)=\prod_{k=1}^{n}P(x_k|\theta) P(D∣θ)=k=1∏nP(xk∣θ)
因此最终求得:
P ( x ∣ D ) = ∫ P ( x ∣ θ ) P ( θ ∣ D ) d θ P(x|D)=\int P(x|\theta)P(\theta|D)d\theta P(x∣D)=∫P(x∣θ)P(θ∣D)dθ
4. 编程实现拉普拉斯修正的朴素贝叶斯分类器,并以西瓜数据集3.0为例(P84),对P151的测试样本1进行判别。
// An highlighted block
import xlrd
import math
class LaplacianNB():
"""
Laplacian naive bayes for binary classification problem.
"""
def __init__(self):
"""
"""
def train(self, X, y):
"""
Training laplacian naive bayes classifier with traning set (X, y).
Input:
X: list of instances. Each instance is represented by
y: list of labels. 0 represents bad, 1 represents good.
"""
N = len(y)
self.classes = self.count_list(y)
self.class_num = len(self.classes)
self.classes_p = {}
#print self.classes
for c, n in self.classes.items():
self.classes_p[c] = float(n+1) / (N+self.class_num)
self.discrete_attris_with_good_p = []
self.discrete_attris_with_bad_p = []
for i in range(6):
attr_with_good = []
attr_with_bad = []
for j in range(N):
if y[j] == 1:
attr_with_good.append(X[j][i])
else:
attr_with_bad.append(X[j][i])
unique_with_good = self.count_list(attr_with_good)
unique_with_bad = self.count_list(attr_with_bad)
self.discrete_attris_with_good_p.append(self.discrete_p(unique_with_good, self.classes[1]))
self.discrete_attris_with_bad_p.append(self.discrete_p(unique_with_bad, self.classes[0]))
self.good_mus = []
self.good_vars = []
self.bad_mus = []
self.bad_vars = []
for i in range(2):
attr_with_good = []
attr_with_bad = []
for j in range(N):
if y[j] == 1:
attr_with_good.append(X[j][i+6])
else:
attr_with_bad.append(X[j][i+6])
good_mu, good_var = self.mu_var_of_list(attr_with_good)
bad_mu, bad_var = self.mu_var_of_list(attr_with_bad)
self.good_mus.append(good_mu)
self.good_vars.append(good_var)
self.bad_mus.append(bad_mu)
self.bad_vars.append(bad_var)
def predict(self, x):
"""
"""
p_good = self.classes_p[1]
p_bad = self.classes_p[0]
for i in range(6):
p_good *= self.discrete_attris_with_good_p[i][x[i]]
p_bad *= self.discrete_attris_with_bad_p[i][x[i]]
for i in range(2):
p_good *= self.continuous_p(x[i+6], self.good_mus[i], self.good_vars[i])
p_bad *= self.continuous_p(x[i+6], self.bad_mus[i], self.bad_vars[i])
if p_good >= p_bad:
return p_good, p_bad, 1
else:
return p_good, p_bad, 0
def count_list(self, l):
"""
Get unique elements in list and corresponding count.
"""
unique_dict = {}
for e in set(l):
unique_dict[e] = l.count(e)
return unique_dict
def discrete_p(self, d, N_class):
"""
Compute discrete attribution probability based on {0:, 1:, 2: }.
"""
new_d = {}
#print d
for a, n in d.items():
new_d[a] = float(n+1) / (N_class + len(d))
return new_d
def continuous_p(self, x, mu, var):
p = 1.0 / (math.sqrt(2*math.pi) * math.sqrt(var)) * math.exp(- (x-mu)**2 /(2*var))
return p
def mu_var_of_list(self, l):
mu = sum(l) / float(len(l))
var = 0
for i in range(len(l)):
var += (l[i]-mu)**2
var = var / float(len(l))
return mu, var
if __name__=="__main__":
lnb = LaplacianNB()
workbook = xlrd.open_workbook("../../数据/3.0.xlsx")
sheet = workbook.sheet_by_name("Sheet1")
X = []
for i in range(17):
x = sheet.col_values(i)
for j in range(6):
x[j] = int(x[j])
x.pop()
X.append(x)
y = sheet.row_values(8)
y = [int(i) for i in y]
#print X, y
lnb.train(X, y)
#print lnb.discrete_attris_with_good_p
label = lnb.predict([1, 1, 1, 1, 1, 1, 0.697, 0.460])
print "predict ressult: ", label
结果:
// An highlighted block
predict ressult: (0.03191920486294201, 4.9158340214165893e-05, 1)#分别为正类概率,父类概率以及分类结果