凸多边形最小面积包围矩形

可以此计算2D图形的OBB

计算几何中有这样一条结果：凸多边形的最小包围矩形至少有一条边与多边形的一条边共线。

暴力算法

遍历每一条边构造包围矩形比较面积大小。说是构造包围矩形，其实只需要投影点到边以及垂直边上取距离最远两点距离得长宽后求面积即可。

算法的全部时间消耗为O(n^2)。

/* min value */
#define FLT_MIN 1.175494351e-38F 
/* max value */
#define FLT_MAX 3.402823466e+38F

struct OBB {
	Point u[2]; //x, y轴
	Point c;	//中心点
	float e[2];	//半长，半宽
};

float MinAreaRec(Point *pts, int ptsNum, OBB &obb) {
	float minArea = FLT_MAX;

	for(int i = 0, j = ptsNum - 1; i < ptsNum; j = i, i++) {//遍历边
		Point u0 = pts[i] - pts[j];//构造边
		u0 = u0/Length(u0);
		Point u1 = Point(0-u0.y, u0.x);//与u0垂直
		float min0 = 0.0f, max0 = 0.0f, min1 = 0.0f, max1 = 0.0f;

		for(int k = 0; k < ptsNum; k++) {//遍历点
			Point d = pts[k] - pts[j];
			//投影在u0
			float dot = Dot(d, u0);
			if(dot < min0) min0 = dot;
			if(dot > max0) max0 = dot;
			//投影在u1
			dot = Dot(d,u1);
			if(dot < min1) min1 = dot;
			if(dot > max1) max1 = dot;
		}

		float area = (max0 - min0) * (max1 - min1);
		if( area < minArea ) {
			minArea = area;
			obb.c = pts[j] + ( u0 * (max0 + min0) + u1 * (max1 + min1) )*0.5f;

			obb.u[0] = u0;
			obb.u[1] = u1;

			obb.e[0] = (max0 - min0)*0.5f;
			obb.e[1] = (max1 - min1)*0.5f;
		}
	}
	return minArea;
}

Point * GetOBBPoints(OBB obb) {//获取OBB四个顶点坐标
	Point *pts = new Point [4];

	pts[0] = obb.c + ( obb.u[0] * obb.e[0] + obb.u[1] * obb.e[1] );
	pts[1] = obb.c + ( obb.u[0] * obb.e[0] - obb.u[1] * obb.e[1] );
	pts[2] = obb.c - ( obb.u[0] * obb.e[0] + obb.u[1] * obb.e[1] );
	pts[3] = obb.c + ( obb.u[1] * obb.e[1] - obb.u[0] * obb.e[0] );

	return pts;
}

旋转卡尺（旋转卡壳）算法

使用旋转卡尺算法可将计算凸多边形的最小包围矩形的时间消耗减少至O(n log n)。

取坐标上两极值点构成平行线，旋转两线，当线与多边形一条边重合时，计算构成矩形面积。

继续旋转，直至旋转角度超过90度。取最小面积。

该算法仅对凸体有效（暴力法对凸体凹体均有效），因此需要先计算凸体，该算法的时间复杂度受限于凸体的计算过程，在确定凸体的前提下，该算法可达O(n)。

 

凸体效果

凹体效果（故先需要对凹体进行凸体计算，凸体计算在此不进行介绍）

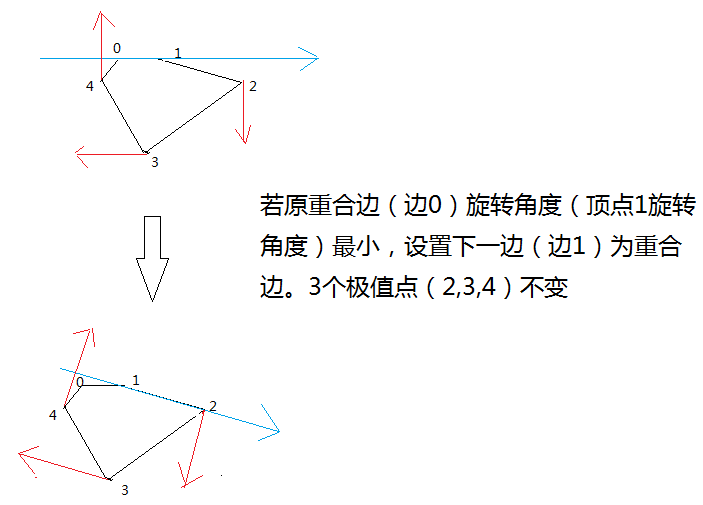
分析：

首先默认一平行边已经与某一边重合（一般我们取第一条边）。

计算以该边方向为x轴方向的xy坐标系（u0，u1）。

则四条边的方向为（u0, u1, -u0, -u1），我们只需要记录其所在的点就可以了。

确定最初的极值点。

 

接下来就是计算该旋转哪条边了。

计算出旋转角度最小的一条边。

旋转角度a的计算：利用已知向量v1，v2，根据Dot（v1，v2） = |v1|*|v2|*cosa计算cosa的值，再由于在角度0~180度之间，角度越大相应cos值越小。

由于旋转的角度在4条边中是最小的，故其他三条边进行相同角度的旋转时，绝对不会与下一条边重合，除非最小角度有两个相同的，但这也不影响计算，因为下次就成旋转角度0（非重合边）的成为重合边，再下次就没有了。不移动的三点为新的极值点，若原重合边旋转角度不是最小，则原来的重合边中后一点成为新的极值点，最小旋转角度的边旋转后碰到的边成为新的重合边。

需要注意的是，以下图为例，

投影在x轴最大的极值点计算与u1角度，而投影在x轴最小的极值点计算与-u1的角度。（负！因为这个失误卡了两天TAT）

同理，投影在y轴最大的极值点计算与-u0角度，而投影在y轴最小的极值点(即重合边中后一点)计算与u0的角度。

计算出角度后，尽管我们根据上边所描述的能够知道有哪几点为极值点。但是我们并不知道哪个点具体是哪个极值点，这时进行重新计算，即投影比较。这里只须计算3点即可。（重合边是投影在y轴最小，无需计算）

重设极值点后进行面积计算，直至u0旋转至回到初始边即可停止（或旋转n次,n为边个数）。

根据最小面积时候的极值点以及xy轴（u0，u1）可以确定obb。

整理步骤如下：

以e0为重合边初始化u0u1;

求3个极值点在pts中下标imax0 imax1 imin0 ;

for(int i = 0; i < ptsNum ; i++) {

    求最小旋转角的顶点的下标；

    if( 0 == 最小旋转角的顶点的下标 )break;

    if(最小旋转角的顶点的下标 == 原3个极值点中的一个) {

        把原重合边后端点设为极值点;

        设置新重合边;

    }

    if(最小旋转角的顶点的下标 == 原重合边后一点) 设置新重合边;

    维护极值点，确定各个极值点为什么的极值点;

    求面积area;

    if(area < minArea) minArea = area;//在此你也可以设置obb

}

float Cos(Point v, Point p1) {
	float dot = Dot(v,p1);
	float cos = dot/(Length(v)*Length(p1));
	return cos;
}

void Setu0u1(Point e, Point &u0, Point &u1) {
	//以e方向为x轴方向，设定xy轴
	u0 = e / Length(e);
	u1 = Point( 0 - u0.y, u0.x);
}

int GetMinAngleIndex(int imin1, int imax0, int imax1, int imin0,
					 Point* e, Point u0, Point u1) {
	//返回旋转角度最小（cos值最大）的点的下标
	int imin_angle_index = 0;

	float cos = 0, maxCos = FLT_MIN;
	cos = Cos(e[imin1], u0);
	if(cos > maxCos){maxCos = cos; imin_angle_index = imin1;}

	cos = Cos(e[imax0], u1);
	if(cos > maxCos){maxCos = cos; imin_angle_index = imax0;}

	cos = Cos(e[imax1], Point(0-u0.x,0-u0.y));
	if(cos > maxCos){maxCos = cos; imin_angle_index = imax1;}

	cos = Cos(e[imin0], Point(0-u1.x,0-u1.y));
	if(cos > maxCos){maxCos = cos; imin_angle_index = imin0;}

	return imin_angle_index;
}

void SetMinMax(Point*pts, int i, int iu, Point u0, Point u1,
			   float &max0, float &min0, float &max1,
			   int & new_imax0, int &new_imin0, int &new_imax1) 
{
	//找到x轴投影最大最小，y轴投影最大的长度（y轴最小则是重合边上点，长度为0）
	//以及极值点在pts中的下标
	Point d =  pts[i] - pts[iu];
	float dist0 = Dot( d, u0);
	if(dist0 > max0){ max0 = dist0; new_imax0 = i;}
	if(dist0 < min0){ min0 = dist0; new_imin0 = i;}

	float dist1 = Dot( d, u1);
	if(dist1 > max1){ max1 = dist1; new_imax1 = i;}
}

float MinAreaRec2(Point *pts, int ptsNum, OBB &obb) {//旋转卡壳算法
	//必须是凸包
	float minArea = FLT_MAX;
	//初始化边e
	Point *e = new Point[ ptsNum ];
	for(int i = 0; i < ptsNum; i++) {
		e[i] = pts[(i+1)%ptsNum] - pts[i];
	}
	int iu = 0;//以e[0]为重合边
	//初始化u0 u1
	Point u0,u1;
	Setu0u1(e[iu], u0, u1);

	int imax0 = 0, imax1 = 0, imin0 = 0, imin1 = 0;
	float min0 = FLT_MAX, max0 = FLT_MIN,
		  max1 = FLT_MIN, min1 = 0;//min1其实可以不需要设定的，始终为0
									//只是为了理解方便加上
									//要去掉则需要把下方用到的min1都改为0
										
	//求三个极值坐标
	for( int i = 0; i < ptsNum; i++) {
		SetMinMax(pts, i, iu, u0, u1,
			   max0, min0, max1,
			   imax0, imin0, imax1) ;
	}

	for(int i = 0; i < ptsNum ; i++) {
		int iminangle = 0;
		iminangle = GetMinAngleIndex((iu+1)%ptsNum, imax0, imax1, imin0, e, u0, u1);
		if(iminangle == 0)break;//旋转回了初始点 没必要继续

		if(iminangle == imax0){imax0 = (iu + 1)%ptsNum;iu = iminangle;}
		else if(iminangle == imax1){imax1 = (iu + 1)%ptsNum;iu = iminangle;}
		else if(iminangle == imin0){imin0 = (iu + 1)%ptsNum;iu = iminangle;}
		else if(iminangle == (iu+1)%ptsNum){iu = (iu+1)%ptsNum;}

		Setu0u1(e[iu], u0, u1);//重设u0u1

		//维护三个极值点
		int new_imax0 = imax0, new_imax1 = imax1, new_imin0 = imin0;
		min0 =FLT_MAX, max0 = FLT_MIN, max1 = FLT_MIN;

		//确定原先imax0在新坐标系中是什么极值
		SetMinMax(pts, imax0, iu, u0, u1,
			   max0, min0, max1,
			   new_imax0, new_imin0, new_imax1) ;
		//确定原先imax1在新坐标系中是什么极值
		SetMinMax(pts, imax1, iu, u0, u1,
			   max0, min0, max1,
			   new_imax0, new_imin0, new_imax1) ;
		//确定原先imin0在新坐标系中是什么极值
		SetMinMax(pts, imin0, iu, u0, u1,
			   max0, min0, max1,
			   new_imax0, new_imin0, new_imax1) ;

		imax0 = new_imax0;
		imax1 = new_imax1;
		imin0 = new_imin0;
		//维护完毕

		//求面积 设置obb
		float area = (max0 - min0)*(max1 - min1);
		if(area < minArea) {
			minArea = area;

			obb.e[0] = (max0 - min0)*0.5f;
			obb.e[1] = (max1 - min1)*0.5f;

			obb.u[0] = u0;
			obb.u[1] = u1;

			obb.c = pts[iu] + ( u0 * (max0 + min0) + u1 * (max1 + min1) )*0.5f;
		}
	}
	

	return minArea;
}