Stanford - Algorithms: Design and Analysis, Part 1 - Week 4 Assignment: strongly connected component

本次作业要求如下：

Question 1

Download the text file  here. Zipped version  here. (Right click and save link as)

The file contains the edges of a directed graph. Vertices are labeled as positive integers from 1 to 875714. Every row indicates an edge, the vertex label in first column is the tail and the vertex label in second column is the head (recall the graph is directed, and the edges are directed from the first column vertex to the second column vertex). So for example, the 11th row looks liks : "2 47646". This just means that the vertex with label 2 has an outgoing edge to the vertex with label 47646

Your task is to code up the algorithm from the video lectures for computing strongly connected components (SCCs), and to run this algorithm on the given graph. 

Output Format: You should output the sizes of the 5 largest SCCs in the given graph, in decreasing order of sizes, separated by commas (avoid any spaces). So if your algorithm computes the sizes of the five largest SCCs to be 500, 400, 300, 200 and 100, then your answer should be "500,400,300,200,100". If your algorithm finds less than 5 SCCs, then write 0 for the remaining terms. Thus, if your algorithm computes only 3 SCCs whose sizes are 400, 300, and 100, then your answer should be "400,300,100,0,0".

WARNING: This is the most challenging programming assignment of the course. Because of the size of the graph you may have to manage memory carefully. The best way to do this depends on your programming language and environment, and we strongly suggest that you exchange tips for doing this on the discussion forums.

这次的作业是相当有难度的，是用kosaraju algorithm求解Strongly Connected Components(SCCs)：

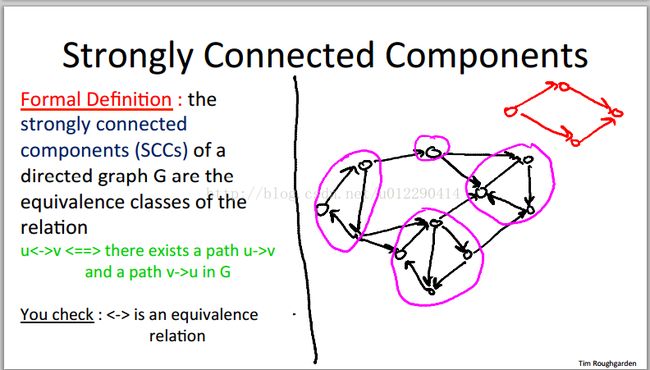
所谓SCCs，下面一张图可以很好地说明：

说白了，就是directed graph中的两个vertex：v和w，v可以到达w，w也可以到达v，他俩就算SCCs

有一种很巧妙的算法可以解决这个问题，就是kosaraju算法，该算法的正确性很难理解，不过好在这也不是本次作业，或者将来大公司技术面试的重点，所以忽略。。

这里只讨论该算法的描述过程，以及如果用C++实现，这个算法的描述其实并不复杂，但是足够神奇：

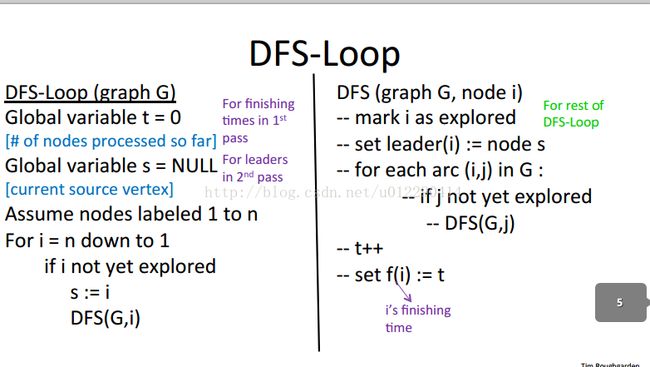
下面两张图大致介绍了该算法的伪代码：

需要对Grev进行一次DFS-loop

然后再对G进行一次DFS-loop

DFS-lopp由下图说明：

下面就针对算法的各个模块说明我的C++实现方式：

1,获得Grev:

我用了一种看起来相当二缺的方式做的，比如我采用adjacency list的方式，从txt导入的时候，如果有一个是1->2，则我在这个后面再设定一个新的adjacency list，存在2->1：

导入的代码如下：

/* store the txt file into adjacency list */
void store_file(map& adjacency_list, map& reverse_list, string filename) {
    ifstream infile;
    infile.open(filename, ios::in);
    int tmp1, tmp2;
    map::iterator it;
    while (infile >> tmp1 >> tmp2) {
        /* tmp1->tmp2 */
        if (adjacency_list.find(tmp1) == adjacency_list.end()) {
            vector tmp_vec(1, tmp2);
            adjacency adj_tmp;
            adj_tmp.visited = false;
            adj_tmp.name = tmp1;
            adj_tmp.list = tmp_vec;
            adjacency_list.insert(pair(tmp1, adj_tmp));
        }
        else {
            adjacency_list[tmp1].list.push_back(tmp2);
        }
        if (adjacency_list.find(tmp2) == adjacency_list.end()) {
            vector tmp_vec(0);
            adjacency adj_tmp;
            adj_tmp.visited = false;
            adj_tmp.name = tmp2;
            adj_tmp.list = tmp_vec;
            adjacency_list.insert(pair(tmp2, adj_tmp));
        }
        if (reverse_list.find(tmp2) == reverse_list.end()) {
            vector tmp_vec(1, tmp1);
            adjacency adj_tmp;
            adj_tmp.visited = false;
            adj_tmp.name = tmp2;
            adj_tmp.list = tmp_vec;
            reverse_list.insert(pair(tmp2, adj_tmp));
        }
        else {
            reverse_list[tmp2].list.push_back(tmp1);
        }
        if (reverse_list.find(tmp1) == reverse_list.end()) {
            vector tmp_vec(0);
            adjacency adj_tmp;
            adj_tmp.visited = false;
            adj_tmp.name = tmp1;
            adj_tmp.list = tmp_vec;
            reverse_list.insert(pair(tmp1, adj_tmp));
        }
    }
    infile.close();
}

2，获得order

首先对Grev进行dfs-loop:

for (map::reverse_iterator rit = reverse_list.rbegin(); rit != reverse_list.rend(); ++rit) {
            if (rit->second.visited == false) {
                int sz = 0;
                dfs(adjacency_list ,reverse_list, rit->second, op, sz);
            }
        }

然后是dfs:

for (int i = 0; i < node.list.size(); ++i) {
            if (reverse_list[node.list[i]].visited == false)
                dfs(adjacency_list, reverse_list, reverse_list[node.list[i]], op, sz);
        }
        stack_list.push(adjacency_list[node.name]);

我是根据完成的时间存进了stack中，这样获得order，方便下一步的使用。

3, Run dfs-loop on G

首先是根据上面的stack中的order进行dfs-loop:

	while (!stack_list.empty()) {
            if (adjacency_list[stack_list.top().name].visited == false) {
                int sz = 1;
                dfs(adjacency_list, reverse_list, stack_list.top(), op, sz);
                size_set.insert(sz);
            }
            stack_list.pop();
        }

然后进行dfs:

	adjacency_list[node.name].visited = true;
        for (int i = 0; i < node.list.size(); ++i) {
            if (adjacency_list[node.list[i]].visited == false) {
                ++sz;
                dfs(adjacency_list, reverse_list, adjacency_list[node.list[i]], op, sz);
            }
        }

以上就是全部过程，

下面是完整代码，这次的代码写的非常之丑，数据结构的使用也没有深思熟虑，时间太赶了，不过这是我的个人代码，不是团队project，就先将就吧。。。

# include 
# include 
# include