AVL树简单了解

1.AVL树定义

在计算机科学中，AVL树是最早被发明的自平衡二叉查找树。在AVL树中，任一节点对应的两棵子树的最大高度差为1，因此它也被称为高度平衡树。

查找、插入和删除在平均和最坏情况下的时间复杂度都是 O(logn)。增加和删除元素的操作则可能需要借由一次或多次树旋转，以实现树的重新平衡。

AVL树得名于它的发明者G. M. Adelson-Velsky和Evgenii Landis，他们在1962年的论文《An algorithm for the organization of information》中公开了这一数据结构。

它具有以下两个性质：

1.任意一个结点的key，比它的左孩子key大，比它的右孩子key小；
2.任意结点的孩子结点之间高度差距最大为1；

2.平衡操作

因为AVL树是一种平衡树，所以每次增加或者减少树中的元素都有可能使这棵树由平衡变得不平衡，所以我们需要一种机制来检测这棵树是否平衡，以及当它不平衡的时候，我们应该通过某些操作使它重新平衡(rebalanced)。

对于一棵树来说，它的高度(height)定义如下：

从根节点(root)开始到某一个叶子节点(leaf)的最长路径(path)上结点的个数

根据AVL树的定义，我们可以为所有的结点定义一个平衡因子(balanced factor)：

某个结点的平衡因子等于该节点的左孩子的高度减去右孩子的高度

根据平衡树的定义，计算得到的平衡因为会出现两种情况：

• 如果平衡因子是0, 1, -1 这三个数的话，可以认定该节点是符合平衡树的定义的；
• 否则，该结点不平衡，需要重新平衡；

对于一个BST来说，每次插入的元素只可能放在叶子结点上。所以只能影响某个子树是否平衡，对其他子树不会有任何的影响。在这种情况下，我们只需要根据搜索的路径，从孩子往祖先找，如果有不平衡的结点就可以被找到。如果一直到根结点都没有发现不平衡结点，则可以认为这次的插入操作没有造成树的不平衡。

重平衡

如果发现了某个不平衡的结点，那么就需要对该结点进行重平衡。实现重平衡的方法，是对该节点的子树进行旋转(rotation)。

旋转之后不会破坏二叉排序树的平衡。

需要平衡的四种情况

case1：LL，左左。插入或删除一个节点后，根节点的左子树的左子树还有非空子节点，导致"根的左子树的高度"比"根的右子树的高度"大2，导致AVL树失去了平衡。
case2：LR，左右。插入或删除一个节点后，根节点的左子树的右子树还有非空子节点，导致"根的左子树的高度"比"根的右子树的高度"大2，导致AVL树失去了平衡。
case3：RL，右左。插入或删除一个节点后，根节点的右子树的左子树还有非空子节点，导致"根的右子树的高度"比"根的左子树的高度"大2，导致AVL树失去了平衡。
case4： RR，右右。插入或删除一个节点后，根节点的右子树的右子树还有非空子节点，导致"根的右子树的高度"比"根的左子树的高度"大2，导致AVL树失去了平衡。

这四种情况，都可以通过一次或者两次的旋转，来使得不平衡的结点变平衡。其中，case1, case4可以通过一次旋转(singly rotation)重新平衡，case2, case3可以通过两次旋转(doubly rotation)重新平衡。

单次旋转(singly rotatioin)

单次旋转得到重新平衡的子树的示意图如下所示，需要注意的是分清对应的结点。

case1：LL，只需执行一次右旋操作。

private AVLTreeNode<T> rightRotation(AVLTreeNode<T> z) {
	AVLTreeNode<T> y;
	y = z.left;
	z.left = y.right;
	y.right = z;

	z.height = max( height(z.left), height(z.right)) + 1;
	y.height = max( height(y.left), z.height) + 1;

	return y;
}

case4：RR，只需执行一次左旋操作

private AVLTreeNode<T> rightRightRotation(AVLTreeNode<T> z) {
	AVLTreeNode<T> y;

	y = z.right;
	z.right = y.left;
	y.left = z;

	z.height = max( height(z.left), height(z.right)) + 1;
	y.height = max( height(y.right), z.height) + 1;

	return y;
}

双次旋转(doubly rotatioin)

双次旋转顾名思义，就是要进行两次旋转来使子树重新平衡，流程如下图示：

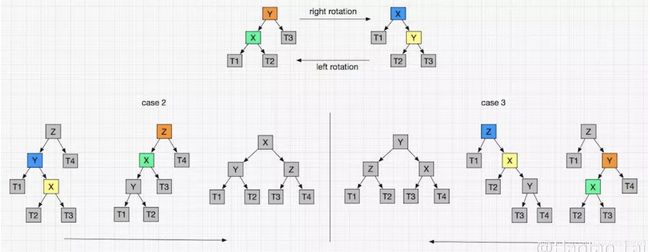
case2：LR，需要先进行一次左旋转，然后再进行一次右旋转；

private AVLTreeNode<T> leftRightRotation(AVLTreeNode<T> z) {
	z.left = leftRotation(z.left);
	return rightRotation(z);
}

case3：RL，需要先进行一次右旋转，然后再进行一次左旋转；

private AVLTreeNode<T> rightLeftRotation(AVLTreeNode<T> z) {
	z.right = rightRotation(z.right);
	return leftRotation(z);
}

3.插入元素(Insert)

标准的BST插入元素操作，找到该元素应该被放置的叶子结点，将该元素连接上去；
检查这次操作是否破坏了树的平衡，若是，通过旋转维护平衡特性；

    /*
     * 将结点插入到AVL树中，并返回根节点
     *
     * 参数说明：
     *     tree AVL树的根结点
     *     key 插入的结点的键值
     * 返回值：
     *     根节点
     */
    private AVLTreeNode<T> insert(AVLTreeNode<T> tree, T key) {
        if (tree == null) {
            // 新建节点
            tree = new AVLTreeNode<T>(key, null, null);
        } else {
            int cmp = key.compareTo(tree.key);

            if (cmp < 0) {    // 应该将key插入到"tree的左子树"的情况
                tree.left = insert(tree.left, key);
                // 插入节点后，若AVL树失去平衡，则进行相应的调节。
                if (height(tree.left) - height(tree.right) == 2) {
                    if (key.compareTo(tree.left.key) < 0)
                        tree = rightRotation(tree);
                    else
                        tree = leftRightRotation(tree);
                }
            } else if (cmp > 0) {    // 应该将key插入到"tree的右子树"的情况
                tree.right = insert(tree.right, key);
                // 插入节点后，若AVL树失去平衡，则进行相应的调节。
                if (height(tree.right) - height(tree.left) == 2) {
                    if (key.compareTo(tree.right.key) > 0)
                        tree = leftRotation(tree);
                    else
                        tree = rightLeftRotation(tree);
                }
            } else {    // cmp==0
                System.out.println("添加失败：不允许添加相同的节点！");
            }
        }

        tree.height = max( height(tree.left), height(tree.right)) + 1;

        return tree;
    }

4.删除元素(Delete)

在一棵树中，删除某个元素，逻辑应该是这样子的：

搜索给定的key，确定其是否在树中；
如果不在树中，返回null；
如果在树中，执行标准的BST删除操作，并返回该删除的结点；
1.如果要删除的节点正好是叶子节点，直接删除就 Ok 了；
2.如果要删除的节点还有子节点，就需要建立父节点和子节点的关系：

• 如果只有左孩子或者右孩子，直接把这个孩子上移放到要删除的位置就好了；
• 如果有两个孩子，就需要选一个合适的孩子节点作为新的根节点，该节点称为继承节点。

然后检查被删除结点的所有祖先结点是否平衡，如果不平衡，则执行重平衡操作

	/*
     * 删除结点(z)，返回根节点
     *
     * 参数说明：
     *     tree AVL树的根结点
     *     z 待删除的结点
     * 返回值：
     *     根节点
     */
    private AVLTreeNode<T> remove(AVLTreeNode<T> tree, AVLTreeNode<T> z) {
        // 根为空 或者 没有要删除的节点，直接返回null。
        if (tree==null || z==null)
            return null;

        int cmp = z.key.compareTo(tree.key);
        if (cmp < 0) {        // 待删除的节点在"tree的左子树"中
            tree.left = remove(tree.left, z);
            // 删除节点后，若AVL树失去平衡，则进行相应的调节。
            if (height(tree.right) - height(tree.left) == 2) {
                AVLTreeNode<T> r =  tree.right;
                if (height(r.left) > height(r.right))
                    tree = rightLeftRotation(tree);
                else
                    tree = leftRotation(tree);
            }
        } else if (cmp > 0) {// 待删除的节点在"tree的右子树"中
            tree.right = remove(tree.right, z);
            // 删除节点后，若AVL树失去平衡，则进行相应的调节。
            if (height(tree.left) - height(tree.right) == 2) {
                AVLTreeNode<T> l =  tree.left;
                if (height(l.right) > height(l.left))
                    tree = leftRightRotation(tree);
                else
                    tree = rightRotation(tree);
            }
        } else {// tree是对应要删除的节点。
            // tree的左右孩子都非空
            if ((tree.left!=null) && (tree.right!=null)) {
                if (height(tree.left) > height(tree.right)) {
                    // 如果tree的左子树比右子树高；
                    // 则(01)找出tree的左子树中的最大节点
                    //   (02)将该最大节点的值赋值给tree。
                    //   (03)删除该最大节点。
                    // 这类似于用"tree的左子树中最大节点"做"tree"的替身；
                    // 采用这种方式的好处是：删除"tree的左子树中最大节点"之后，AVL树仍然是平衡的。
                    AVLTreeNode<T> max = maximum(tree.left);
                    tree.key = max.key;
                    tree.left = remove(tree.left, max);
                } else {
                    // 如果tree的左子树不比右子树高(即它们相等，或右子树比左子树高1)
                    // 则(01)找出tree的右子树中的最小节点
                    //   (02)将该最小节点的值赋值给tree。
                    //   (03)删除该最小节点。
                    // 这类似于用"tree的右子树中最小节点"做"tree"的替身；
                    // 采用这种方式的好处是：删除"tree的右子树中最小节点"之后，AVL树仍然是平衡的。
                    AVLTreeNode<T> min = minimum(tree.right);
                    tree.key = min.key;
                    tree.right = remove(tree.right, min);
                }
            } else {
                AVLTreeNode<T> tmp = tree;
                tree = (tree.left!=null) ? tree.left : tree.right;
                tmp = null;
            }
        }

        if(tree != null)
            tree.height = max(height(tree.left), height(tree.right)) + 1;
        return tree;
    }

5.测试结果

== 依次添加: 3 2 1 4 5 6 7 16 15 14 13 12 11 10 8 9 
== 前序遍历: 7 4 2 1 3 6 5 13 11 9 8 10 12 15 14 16 
== 中序遍历: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 
== 后序遍历: 1 3 2 5 6 4 8 10 9 12 11 14 16 15 13 7 
== 高度: 5
== 最小值: 1
== 最大值: 16
== 树的详细信息: 
 7 is root
 4 is  7's   left child
 2 is  4's   left child
 1 is  2's   left child
 3 is  2's  right child
 6 is  4's  right child
 5 is  6's   left child
13 is  7's  right child
11 is 13's   left child
 9 is 11's   left child
 8 is  9's   left child
10 is  9's  right child
12 is 11's  right child
15 is 13's  right child
14 is 15's   left child
16 is 15's  right child

== 删除根节点: 4
== 高度: 5
== 中序遍历: 1 2 3 5 6 7 8 9 10 11 12 13 14 15 16 
== 树的详细信息: 
 7 is root
 5 is  7's   left child
 2 is  5's   left child
 1 is  2's   left child
 3 is  2's  right child
 6 is  5's  right child
13 is  7's  right child
11 is 13's   left child
 9 is 11's   left child
 8 is  9's   left child
10 is  9's  right child
12 is 11's  right child
15 is 13's  right child
14 is 15's   left child
16 is 15's  right child

完整代码

https://github.com/alinainai/test_11/tree/master/src/avltree

推荐

可以看到 AVL 树的可视化，做的非常到位，强烈推荐
https://www.cs.usfca.edu/~galles/visualization/AVLtree.html
红黑树
https://blog.csdn.net/u013728021/article/details/84303748

参考：
https://www.cnblogs.com/skywang12345/p/3577479.html#a1
https://zh.wikipedia.org/wiki/AVL%E6%A0%91 有墙
https://www.jianshu.com/p/65c90aa1236d 代码有误
https://blog.csdn.net/juanqinyang/article/details/51418863