递归与动态规划专题

介绍递归和动态规划

暴力递归：

1，把问题转化为规模缩小了的同类问题的子问题
2，有明确的不需要继续进行递归的条件(base case)
3，有当得到了子问题的结果之后的决策过程
4，不记录每一个子问题的解

动态规划

1，从暴力递归中来
2，将每一个子问题的解记录下来，避免重复计算
3，把暴力递归的过程，抽象成了状态表达
4，并且存在化简状态表达，使其更加简洁的可能

在学习的第一步，我们只需要先搞清楚递归的前三项。什么是递归
这里引入一个简单的例子 二分法求数组内最小值来让大家对递归函数的写法和思路有一个基本理解。

public class 二分法求数组内最小值 {
    public static void main(String[] args) {
        int arr[]={6,8,5,3,2,9,7,6,3};
        System.out.println(getMin(arr, 0, arr.length-1));
    }
    /*
     * 在数组获取最小值 你可以把数组一分为二 然后在分出来的数组内继续求最小值
     * 分出来的数组也继续分，在分段内求最小值。
     * 这就是递归函数的第一个步骤
     * 1，把问题转化为规模缩小了的同类问题的子问题
     */
    public static int getMin(int arr[],int left,int right){
        /*
         * 这一步，就是递归函数的base case也就是跳出条件，递归函数的第二个步骤
         * 这个是任何递归函数都必须具有的，它必须可以跳出，如果不写这个就相当于在循环不写控制条件，这个函数就无尽递归
         * 写base case需要你分析，问题究竟分到什么规模就不可再分了。
         * 比如这个求数组内最小值，我已经将数组分割成了长度为1的数组，那么显然就不需要再进行分割了
         * 因为数组内只有一个元素，那么我们默认他就是最小值，然后通过递归栈递归回去
         */
        if (left==right) {
            return arr[left];
        }
        int mid=(left+right)/2;//分割
        int minLeft=getMin(arr, left, mid);//子问题1
        int minRight=getMin(arr, mid+1, right);//子问题2

        return Math.min(minLeft, minRight);//有了子问题之后的解决过程 也就是递归函数的第三个步骤
    }

}

关于第四特点，现在先不用理解。先看懂上面这个递归函数。非常简单是吧。
下面还有一个非常简单也非常经典的例子，递归求阶乘

public class Code_01_Factorial {
    public static long getFactorial1(int n) {
        if (n == 1) {//2.base case 什么规模我不用再做划分
            return 1L;
        }
        return (long) n * getFactorial1(n - 1);//1.子问题f(n)=n*f(n-1) 3.递归决策  乘以当前值返回
    }
    public static void main(String[] args) {
        int n = 5;
        System.out.println(getFactorial1(n));
    }

}

代码就不贴了。
下面这个题，就要让你建立一个从暴力递归到动态规划的基本思想

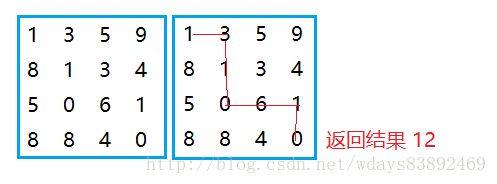
最小路径和问题

给你一个二维数组，二维数组中的每个数都是正数，要求从左上
角走到右下角，每一步只能向右或者向下。沿途经过的数字要累
加起来。返回最小的路径和。

public class 暴力递归求minPath {
    //纯暴力递归的版本
    public static int minPath(int[][] matrix) {
        //递归函数
        return process(matrix, 0, 0);
    }
    /*
     * 我们要推出从左上到右下的最短代价 那么base应该就是右下角坐标(matrix.length-1, matrix[0].length-1)所对应的代价
     * 这段函数从(0,0)位置进入，
     * 我们先考虑每个点在矩阵中的三种情况
     * case 1:最后一列上,那么我只能向下找路
     * case 2:最后一行上,那么我只能向右找路
     * case 3:是一个普遍位置,那么我可以向右 向下两个方向找路
     */
    public static int process(int[][] matrix, int i, int j) {
        //base case 我们要推出从左上到右下的最短代价 那么base应该就是右下角坐标(matrix.length-1, matrix[0].length-1)所对应的代价
        //这个位置必然要加入代价中，所以直接返回         
        if (i == matrix.length-1 && j == matrix[0].length-1) {
            return matrix[i][j];
        }
        //i和j起码有一个没有到终止位置
        if (i == matrix.length-1) {//case 1 子过程1
            return matrix[i][j] + process(matrix, i, j + 1);//j+1向下找路
        }
        if (j == matrix[0].length-1) {//case 2 子过程2
            return matrix[i][j] + process(matrix, i + 1, j);//i+1向上找路
        }
        //向前位置的代价加上向上或者向下位置中较小的那个代价，就是下一个可能存在的最小位置 子过程3
        return matrix[i][j] + Math.min(process(matrix, i, j + 1), process(matrix, i + 1, j));//决策问题过程
    }



    public static void main(String[] args) {
        int[][] m = { { 1, 3, 5, 9 }, { 8, 1, 3, 4 }, { 5, 0, 6, 1 }, { 8, 8, 4, 0 } };
        System.out.println(minPath(m));
    }
}

通过上面的代码在体会一下 递归的那几个特征：

1. 子问题
2. base case
3. 决策过程

很简单就将问题求解了，但是暴力递归是存在缺陷的
这里我们用一个小规模的样例数据来看，暴力递归的缺陷在哪

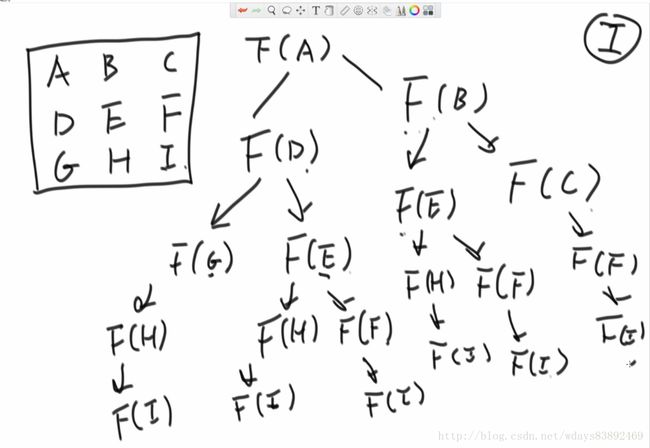
在这样一个图中，你可以看到每一个位置可以怎么选下一步位置
A E都是常规位置，有两种选择 其他的点都在边界上只有一种选择
常规情况应该是常规位置很多，但在这简化模型便于理解

现在就要用到最开始说过的暴力递归的第四个特征，不记录子问题的解。
这是什么意思呢，拿上面的图举例

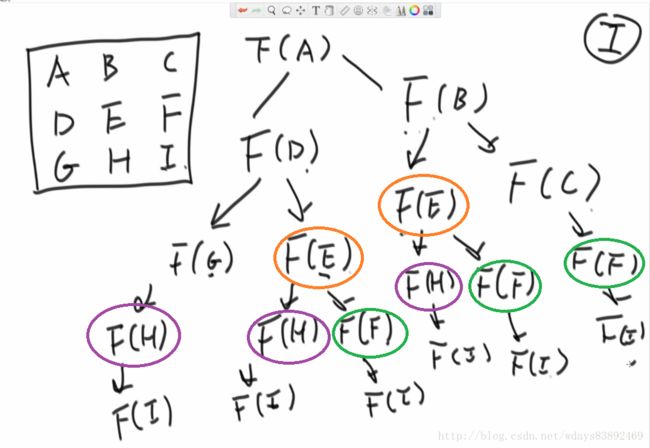
我圈中的部分，都经历了重复运算，比如我D位置的时候找过E，我在B位置又要找一遍E，及其子过程，这个方法是极其浪费时间的 时间复杂度O(2^n)
那么我们怎么去优化它呢。
可以用到这样一个技巧 记忆化搜索(傻缓存)

//伪代码描述
HashMap<String,Integer> cache=new HashMap<String,Integer>();
int res=matirx[i][j];
计算最短路径
return res;
将位置与res所代表的值填入HashMap中
以后递归找路的过程中，先查cache中是否存在，如果存在，那么就直接取，不存在，就计算，然后存入cache。

它是不在乎先后次序的，先查，没有就算，有就取，所以也叫傻缓存
已经初步具备了动态规划的思想。
想尝试的可以用这种方法改写之前暴力递归的代码。
通过这个过度。对动态规划应该有一个概念，那就是空间换时间。我将暴力递归的子过程的值存储下来，那么就可以把时间复杂度从 O(2^n) 降至 O(n^2)

动态规划

所有的动态规划，都是由暴力递归改写而成的，这是个高度套路的方法。
而且，写出暴力递归的版本之后，算法就已经完全和题目解耦。思考怎么写动态规划不用再去思考原问题，只需要分析暴力递归函数。
刚才傻缓存的方法是不关心依赖顺序的。只是很简单查，有就用，没有就算。
当你开始关心依赖顺序，那么就已经是动态规划的方法了。

1. 分析可变参数（解空间）；
2. 确定最终状态；
3. 根据basecase确定初始状态；
4. 分析普遍位置依赖哪些位置；
5. 根据依赖顺序逆序求整张表。

推位置依赖的方法

1. 分析递归函数
   看这个函数有那些可变参数，知道这些参数那么解一定固定，也就是哪些参数可以代表解的状态

   之前暴力递归的过程函数是process(int[][] matrix, int i, int j)
   分析这个函数我们就可以知道 当 i 和 j 的值确定，那么返回值一定确定。也就是说
   不管之前是怎么到( i , j )这个位置的，但是从得到( i , j )这个位置后最短距离一定固定。

2. 建立解空间
   根据之前递归函数的可变参数
   一个参数就是一维表，两个参数就是二维表，三个参数就是三维表……甚至有可能能用map
   然后建立解空间。
   比如最短路径这道题 递归函数和两个参数有关，那么就建立一张和原二维数组大小相等的解空间表。
   确定目标，然后推出点的值
   
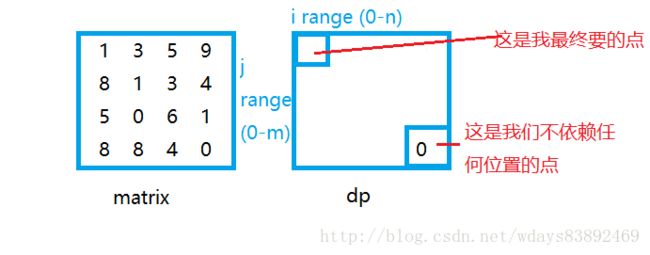
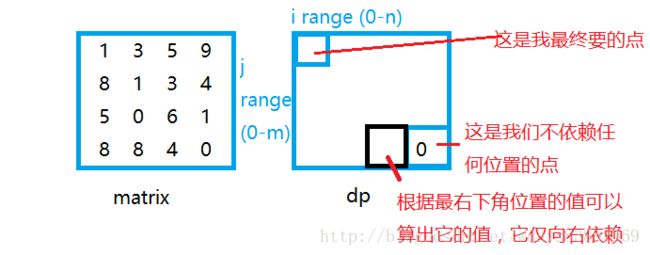
   不需要任何依赖的这个位置右下角，值就是原matrix中右下角的值。
   然后怎么推出dp表中其他位置的的值
   
   最右下角的值是确定的，右下角横坐标-1位置的值只依赖右边的值，那么它的值也可以推算出来。
   
   同理可以算出最下面一行的值。
   
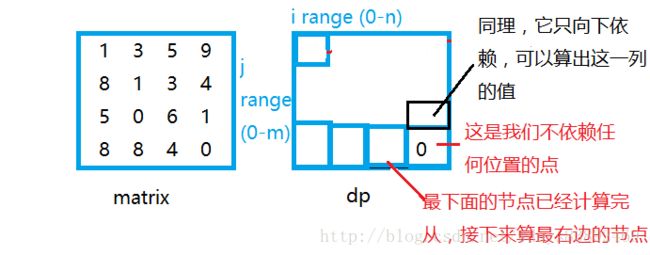
   最下一行和最右一列的值都确定了，那么如何确定一个普遍位置的值
   
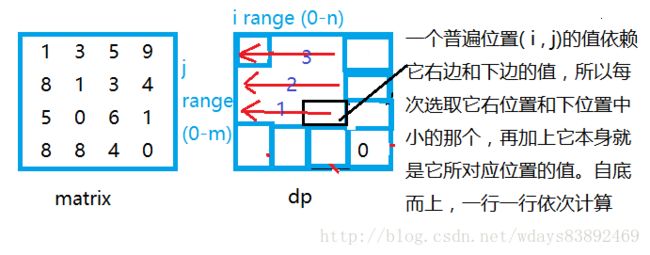
   这样，dp表就算完了，计算出的最后一个(0 , 0)位置的值就是我们要得到的那个值。

public class 动态规划求minPath {

    public static int minPath(int[][] martix) {
        if (martix == null || martix.length == 0 || martix[0] == null || martix[0].length == 0) {//空矩阵
            return 0;
        }
        int row = martix.length;
        int col = martix[0].length;
        int[][] dp = new int[row][col];
        for (int i = 1; i < row; i++) {
            dp[i][0] = dp[i - 1][0] + martix[i][0];//最后一行
        }
        for (int j = 1; j < col; j++) {
            dp[0][j] = dp[0][j - 1] + martix[0][j];//最后一列
        }
        for (int i = 1; i < row; i++) {
            for (int j = 1; j < col; j++) {
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + martix[i][j];//普遍位置
            }
        }
        return dp[row - 1][col - 1];
    }


    public static void main(String[] args) {
        int[][] m = { { 1, 3, 5, 9 }, { 8, 1, 3, 4 }, { 5, 0, 6, 1 }, { 8, 8, 4, 0 } };
        System.out.println(minPath(m));
    }
}

你搜动态规划的解法，都只会给你这样一个代码，但是不会告诉你它究竟是怎么得出的。
我们在学习动态规划的时候一上来就接触局部最优解 全局最优解 状态转移方程。没有经历这样一个过程从而导致的理解困难。但是只要熟悉这种推到方式，在写出暴力递归以后就可以高度套路化的解决此类问题。

扩展内容

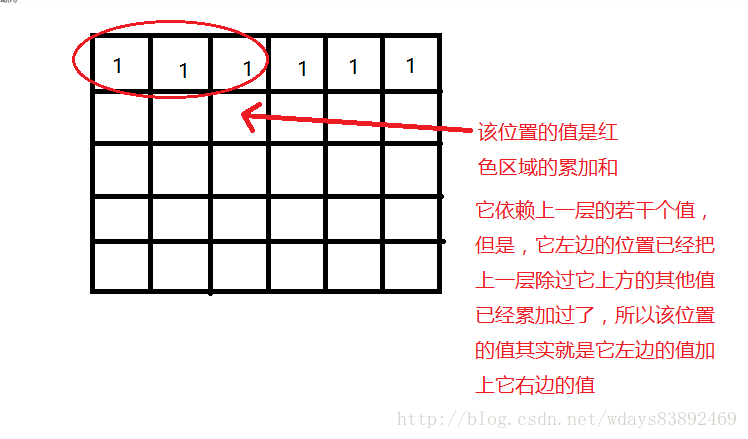
依赖关系的感觉
比如一个二维数组，第一行内容是给定的(base case)
从第二行开始，它每个值都是它上一行的值累加到它的位置。

小明参加了学校的趣味运动会，其中的一个项目是：跳格子。

地上画着一些格子，每个格子里写一个字，如下所示：（也可参见p1.jpg）

从我做起振
我做起振兴
做起振兴中
起振兴中华

比赛时，先站在左上角的写着“从”字的格子里，可以横向或纵向跳到相邻的格子里，但不能跳到对角的格子或其它位置。一直要跳到“华”字结束。

要求跳过的路线刚好构成“从我做起振兴中华”这句话。

请你帮助小明算一算他一共有多少种可能的跳跃路线呢？

附加题

给你一个数组arr，和一个整数aim。如果可以任意选择arr中的
数字，能不能累加得到aim，返回true或者false

最后动态规划还可以用来解决01背包问题。这个我会在之后背包，动态规划，贪心的结合专题文章继续深入探讨