回溯算法-子集树/排列树

子集树

问题描述：在含有n个元素的集合s中，选择l个元素构成的子集；解空间$2^n$，因为每个元素均有两种可能，即被选或者不被选，故共$2^n$种可能。
对应问题：0-1背包问题
子集树角度：问题是从含有n个元素的集合s中选择满足某些条件的元素构成子集，那么该问题的解构成的空间即子集树。
- 子集树共n层(s集合元素个数),第t层表示集合s中的第t个元素选择还是不选择；
- 共$2^n$个叶节点，$2^{n+1}-1$个节点，每个叶节点表示一种解；
- 时间复杂度为$O(2^n)$

伪代码：

 void dfs(int t){//检查集合s中的第t个元素
	 if (t >= n){ //集合s中n个元素均检查完了
	 	handle(path)//根据当前从根节点到叶节点的路径是否符合要求处理返回
	 }
	 else {
		 //构建l层的子集树，在n个元素中选择l个元素
		 for (int i = 0; i < l; i++) {
			 path.add(s[t-1])//选择第t个元素
			 if(第t层(t个元素)满足约束)) 
				dfs(t+1)//回溯t+1层(检查第t+1个元素)
			 path.remove(s[t])//不选择第t个元素 
		 }
	 } 
}

Leetcode题解

• 77:Combination
  题目:
  给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

class Solution {
public:
    vector> combine(int n, int k) {
		vector path;
		vector> result;
		dfsII(1, k, n, path, result);
		return result;
	}
	// way1:未简化的dfs
	void dfsI(int pos,int k,int n,vector& path,vector>& res) {
		if (path.size() == k) {
			res.push_back(path);
            return;
		}
		for (int i = pos; i <= n; i++) {
			path.push_back(i);
			dfsI(i + 1, k, n, path, res);
			path.pop_back();
		}
	}
	// way2:简化后的dfs
	void dfsII(int pos, int k, int n, vector& path, vector>& res) {
		if (path.size() == k) {
			res.push_back(path);
            return;
		}
		// k-path.size()表示还需要的数目,i表示当前的层数
		for (int i = pos; i <= n - (k - path.size())+1; i++) {//作用是在[i,n]之间找到k-path.size()个元素
			path.push_back(i);
			dfsII(i + 1, k, n, path, res);
			path.pop_back();
		}
	}
};

• 78:Subsets

class Solution {
public:
    vector> subsets(vector& nums) {
        //先排序
		 sort(nums.begin(), nums.end());
		 vector> res;
		 vector path;
		 dfs(nums, 0,path, res);
		 return res;
    }
    
    void dfs(vector& nums,int pos, vector& path, vector>& res) {
		 //路径path压栈到result
		 res.push_back(path);
		 
		//构建层数分别为1-nums.size()的子集树
		 for (unsigned int  i = pos; i < nums.size(); i++) {
			path.push_back(nums[i]);//选择nums[i]
			dfs(nums,i+1, path, res);//判断nums中第i+1个元素
			path.pop_back();//不选择nums[i]
		 }
	 }
};

• 90:Subsets II

class Solution {
 public:
	 vector> subsetsWithDup(vector& nums) {
		 //先排序
		 sort(nums.begin(), nums.end());
		 vector> res;
		 vector path;
		 dfs(nums, 0,path, res);
		 return res;
	 }
	 void dfs(vector& nums,int pos, vector& path, vector>& res) {
		 //路径path压栈到result
		 res.push_back(path);

		 for (unsigned int  i = pos; i < nums.size(); i++) {
			 //排序的好处(跳过重复元素）
			if (i > pos && nums[i] == nums[i - 1]) 
				continue;
			path.push_back(nums[i]);//选择nums[i]
			dfs(nums,i+1, path, res);//判断nums中第i+1个元素
			path.pop_back();//不选择nums[i]
		 }
	 }
 };

排列树

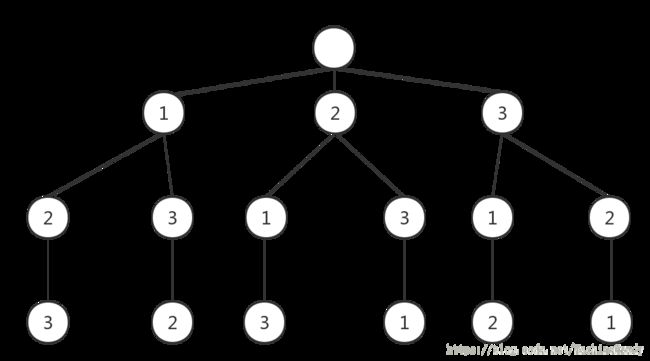
问题描述：对含有n个元素的集合s排序之后构成的集合；解空间$n!$。
对应问题：旅行员售货问题(正权图中找到权重和最小的曼哈顿回路【制指定起点和重点，不重复的经过每一个节点】)
子集树角度：问题是找到对n个元素的集合s中所有元素排序中满足条件的排序，那么该问题的解构成的空间即子集树。
- 共$n!$个叶节点，$2^{n+1}-1$个节点，每个叶节点表示一种解；
- 时间复杂度为$O(n!)$

伪代码:

 void dfs(int t){//对集合s中的第t个元素排序
	 if (t >= n){ //集合s中n个元素已经排序完成
	 	handle(path)//根据当前排序是否符合要求返回
	 }
	 else {
		 for (int i = t; i < s.size(); i++) {
			 swap(s[t],s[i]) //交换第t个元素和其后所有元素
			 if(交换t和i元素之后满足约束)) 
				dfs(t+1) //对第t+1个元素排序
			 swap(s[t],s[i]) //交换回来
		 }
	 } 
}

• Leetcode 46:Permutation

class Solution {
public:
    vector > permute(vector &num) {
        vector > results;
        dfs(0,num,results);
        return results;
    }
    //*l:记录当前取得是当前下标为l的元素
    void dfs(int t,vector &num,vector > &results){
        if(t+1==num.size()){
            results.push_back(num);
            return;
        }else{
            for(int i=t;i

• Leetcode 47:Permutation II

class Solution {
public:
	vector> permuteUnique(vector& nums) {
		//先排序
		sort(nums.begin(), nums.end());
		vector> result;
		vector temp;
		vector visit(nums.size());
		dfs(0, nums.size(), nums, visit,temp, result);
		return result;
	}
	void dfs(int t,int n, vector nums,vector& visit,vector& temp,vector>& result) {
        if (t+1 == n) {
			result.push_back(nums);
			return;
		}
        for(int i=t;i

• 51:NQUEENS
• 784:字母大小写全排列
• 401:二进制手表
• 22:括号生成
• 阿里笔试题目(参考资料中)

参考

Leetcode 回溯法 (持续更新)
位运算角度解Leetcode78子集树
子集树与排列树