用java实现归并排序算法

用java实现归并排序

一. 归并排序的思路

归并排序通过不断的将原数组进行拆分(通常拆分成左右两项)，一直到剩下一项，然后分别将拆分的子数组进行合并，此时，两个子数组已经是排好序的，所以合并排序只需要进行一趟排序即可完成，所以此类排序需要两个步骤：1.拆分原数组
2.合并子数组。因此此算法是经典的分治算法。

拆分算法的思路

利用递归，不断得寻找左子数组和右子数组，一直到数组的长度为一

合并算法的思路

每次合并需要子数组A,B，并新创建一个临时数组C，同时需要三个计数器Actr，Bctr和Cctr，其中Actr和Bctr用来判断数组是否用完，如果用完，则将剩余的数组元素按顺序放入临时数组中。全部放完后，将临时数组中的已经排好顺序的元素更新到原数组中。

二. java代码如下

public class MergeSort {
    public static void main(String[] args) {
        int[] ans = {6, 8, 4, 4, 6, 36, 673, 13, 6, 7, 3, 4, 6, 8, 3, 7, 5, 7, 9, 5};
        System.out.print("原数组：");
        for (int i = 0; i < ans.length; i++) {
            System.out.print(ans[i]+",");
        }
        System.out.println();
        mergeSort(ans);
        System.out.print("归并排序之后的数组：");
        for (int i = 0; i < ans.length; i++) {
            System.out.print(ans[i]+",");
        }
    }

    //sort方法的驱动程序
    private static void mergeSort(int[] ans) {
        sort(ans, 0, ans.length - 1);
    }

    //将tmp和Cctr当做参数传入，方便调用merge方法时获得这两个参数
    private static void sort(int[] ans, int left, int right) {
        int mid = (left + right) / 2;
        //当分到只剩下一个元素的情况,则退出递归程序
        if (left >= right) {
            return;
        }
        sort(ans, left, mid);
        sort(ans, mid + 1, right);
        merge(ans, left, mid, right);
    }

    private static void merge(int[] ans, int left, int mid, int right) {
        //声明三个计时器
        int Actr = left;
        int Bctr = mid + 1;
        int Cctr = 0;
        int lenA = mid - left + 1;
        int lenB = right - mid;
        //创建临时数组,长度为A，B数组长度之和
        int[] tmp = new int[right - left + 1];
        //循环A，B中长度较短的长度次数的二倍的次数
        while (Actr <= mid && Bctr <= right) {
            if (ans[Actr] <= ans[Bctr]) {
                tmp[Cctr++] = ans[Actr];
                Actr++;
            } else {
                tmp[Cctr++] = ans[Bctr];
                Bctr++;
            }
        }
        //如果左边的还有剩余，将左边剩余的归并
        while (Actr <= mid){
            tmp[Cctr ++] = ans[Actr ++];
        }
        //如果右边的还有剩余，将右边剩余的归并
        while (Bctr <= right){
            tmp[Cctr ++] = ans[Bctr ++];
        }
        //将临时数组更新到原数组
        for (int i = 0; i < tmp.length; i++) {
            ans[left++] = tmp[i];
        }
    }
}

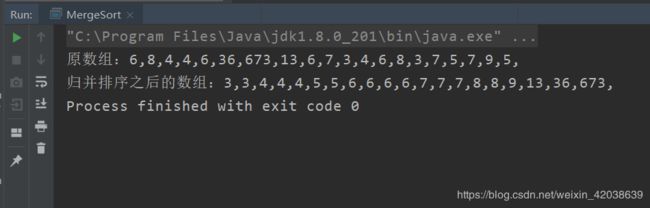
三. 运行结果如下：

四. 时间复杂度

归并排序的最坏时间复杂度和平均时间复杂度均为O(nlogn)

五. 归并排序的应用

归并排序是所有流行的排序算法中比较次数最少的排序算法，在Java类库中的泛型排序就是使用的归并排序(因为泛型类的比较所消耗的时间占比更多),而对于Java类库中的基本类型排序则是使用的快速排序算法