交叉熵损失函数整理
文章目录
- 一.交叉熵函数的由来(推导)
- 1.1普通推导交叉熵 :
- 1.2极大似然推导交叉熵:
- 二.交叉熵函数直观理解
- 三.交叉熵的两种不同形式
- 3.1 Sigmoid + Cross-entropy
- 3.2 SoftMax + Cross-entropy
- 四.交叉熵函数求导
- 4.1 Sigmoid + Cross-entropy
- 4.2 SoftMax + Cross-entropy
- 六.优缺点
- 七.为什么逻辑回归不用MSE而用交叉熵
一.交叉熵函数的由来(推导)
1.1普通推导交叉熵 :
我们一共有m组已知样本, ( x ( i ) , y ( i ) ) (x^{(i)},y^{(i)}) (x(i),y(i))表示第i组数据及其对应的类别标记,
其中 x ( i ) = ( 1 , x 1 i , x 2 i , x 3 i … x p i ) x^{(i)} = (1, x^{i}_1,x^{i}_2,x^{i}_3…x^{i}_p) x(i)=(1,x1i,x2i,x3i…xpi), y ( i ) y^{(i)} y(i)则为表示类别的一个数:
- logistic回归(二分类问题)中, y ( i ) y(i) y(i)取0或者1;
- softmax回归 (多分类问题)中, y ( i ) y(i) y(i)取1,2…k中的一个表示类别标号的一个数(假设共有k类)


以上来自交叉熵代价函数(损失函数)及其求导推导 (Logistic Regression)
1.2极大似然推导交叉熵:
二.交叉熵函数直观理解
单个样本的交叉熵损失函数(注意这里是用单个样本做例子,因此公式里没有 Σ \Sigma Σ):
L o s s = − [ y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) ] Loss = - [ylogŷ + (1-y)log(1-ŷ)] Loss=−[ylogy^+(1−y)log(1−y^)]
其中 y ^ ŷ y^表示真实值,y表示预测值
- 当 y = 1 y=1 y=1时: L o s s = − l o g y ^ Loss = -logŷ Loss=−logy^
这时候,Loss与预测输出的关系如下图所示:
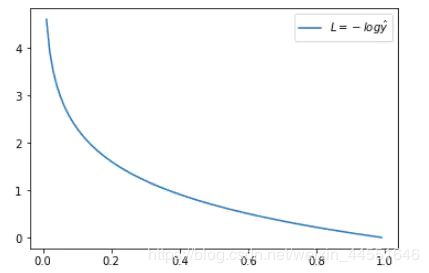
横坐标是预测输出,纵坐标是交叉熵损失函数 L。显然,预测输出越接近真实样本标签 1,损失函数 L 越小;预测输出越接近 0,L 越大。因此,函数的变化趋势完全符合实际需要的情况。 - 当 y = 0 y = 0 y=0 时: L o s s = − l o g ( 1 − y ^ ) Loss = -log(1- ŷ) Loss=−log(1−y^)
这时候,Loss 与预测输出的关系如下图所示:
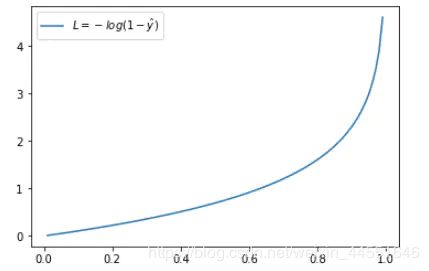
同样,预测输出越接近真实样本标签 0,损失函数 L 越小;预测函数越接近 1,L 越大。函数的变化趋势也完全符合实际需要的情况。
从上面两种图,可以帮助我们对交叉熵损失函数有更直观的理解。无论真实样本标签 y 是 0 还是 1,L 都表征了预测输出与 y 的差距。
从损失函数中我们可以知道交叉熵是用来描述两个分布的距离的,而神经网络训练的目的就是使 预测值ŷ 逼近 真实值y。
三.交叉熵的两种不同形式
- − [ y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) ] - [ylogŷ + (1-y)log(1-ŷ)] −[ylogy^+(1−y)log(1−y^)]
- − y l o g y ^ -ylog ŷ −ylogy^
这两个都是交叉熵损失函数,但是看起来长的却有天壤之别。这是因为这两个交叉熵损失函数对应不同的最后一层的输出:第一个对应的最后一层是sigmoid,第二个对应的最后一层是softMax。 下面会具体解释Sigmoid + Cross-entropy 和 SoftMax + Cross-entropy。
3.1 Sigmoid + Cross-entropy
用sigmoid函数作为神经元的激活函数时,最好使用交叉熵代价函数而不用均方误差损失函数,以避免训练过程太慢
为什么呢?
如果使用均方误差损失函数时:
C = ( y − a ) 2 2 C = \frac{(y-a)^2}{2} C=2(y−a)2
其中, y y y为真实值, a a a为预测值, a = σ ( z ) a = \sigma(z) a=σ(z) , z = w x + b z = wx +b z=wx+b ,所以 a = σ ( w x + b ) a = \sigma(wx + b) a=σ(wx+b)
用链式法则来求权重和偏置的偏导数得:
∂ C ∂ w = ( a − y ) σ ′ ( z ) x = a σ ′ ( z ) \frac{\partial C}{\partial w} = (a - y) \sigma'(z)x = a\sigma'(z) ∂w∂C=(a−y)σ′(z)x=aσ′(z)
∂ C ∂ b = ( a − y ) σ ′ ( z ) = a σ ′ ( z ) \frac{\partial C}{\partial b} = (a - y) \sigma'(z) = a\sigma'(z) ∂b∂C=(a−y)σ′(z)=aσ′(z)
而梯度下降更新规则为:
w = w − η ∂ C ∂ w w = w - \eta\frac{\partial C}{\partial w} w=w−η∂w∂C
b = b − η ∂ C ∂ b b = b - \eta\frac{\partial C}{\partial b} b=b−η∂b∂C
由 sigmoid 函数的图像我们可以知道,当 z 很小 ( 远小于0 ) 或者 z 很大 ( 远大于0 ) 时,σ′(z) 趋于 0,所以代价函数对于 w 和 b 的偏导数就会很小。也可以从下图的sigmoid求导后的图像可以看出,最大值只有0.25,所以 w 和 b 就会产生的变化很小,故,学习缓慢。
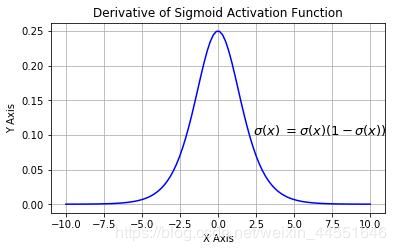
而使用交叉熵作代价函数时:
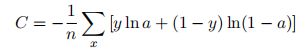
其用链式法则来求权重和偏置的偏导数就有:
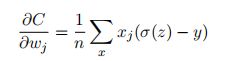
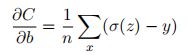
σ′(z) 在链式求导时被约去了,所以不会出现学习缓慢的问题 (除非在最后结果收敛的时候) 。它告诉我们权重学习的速度受到 σ(z) − y,也就是输出中的误差的控制。更大的误差,会有更快的学习速度。这是我们期待的结果,比如现实生活中,如果你犯了很大的错误,肯定会知道应该更要往正确的方向学习,因此学习速度大大提升。
3.2 SoftMax + Cross-entropy
多分类是指分类任务中有多个类别, 比如对一堆水果图片分类, 它们可能是橘子、苹果、梨. 多类分类是假设每个样本都被设置了一个且仅有一个标签: 一个水果可以是苹果或者梨, 但是同时不可能是两者。
因此用真实值y用one-hot表示方法表示出来: [ 0 , 0 , 1 ] [0,0,1] [0,0,1]1表示图片属于这个类别,0则表示图片不属于这个类别。
那为什么在多分类问题中通常使用SoftMax + Cross-entropy的组合方式呢?因为softmax 函数,它可以将一个N维的实数向量压缩成一个满足特定条件的N维实数向。压缩后的向量满足两个条件:
- 向量中的每个元素的大小都在[0,1]
- 向量所有元素的和为 1
比如预测一张图片属于橘子、苹果、梨等的概率,经过softMax函数之后y值变为 [ 0.1 , 0.5 , 0.4 ] [0.1,0.5,0.4] [0.1,0.5,0.4]
可以看到y值都在区间[0,1],且之和为1.
经过softMax函数之后的输出的预测值概率矩阵与经过one-hot编码后的真实值矩阵相对应:
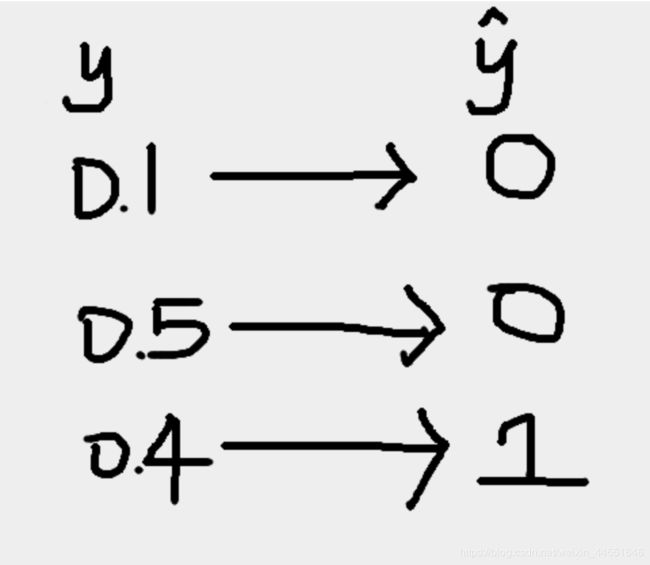
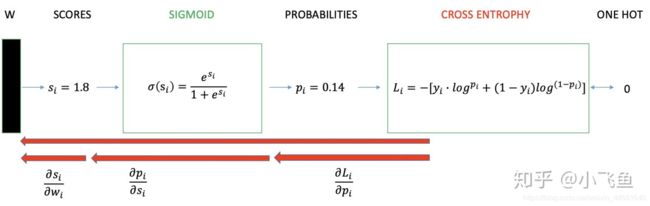
具体步骤如下图所示:
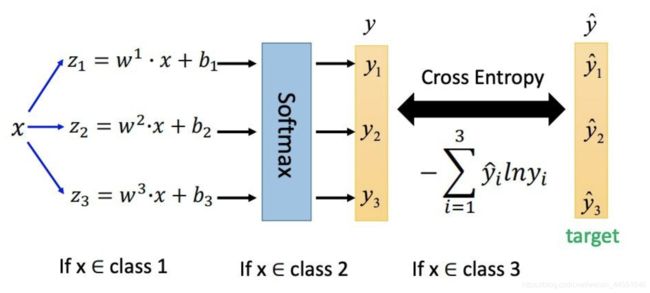
在这里softMax更像是一个激活函数而不是损失函数
四.交叉熵函数求导
4.1 Sigmoid + Cross-entropy
4.2 SoftMax + Cross-entropy
求导
举个例子,通过若干层的计算,最后得到的某个训练样本的向量的分数是 [ z 4 , z 5 , z 6 ] = [ 2 , 3 , 4 ] [z4,z5,z6] = [ 2, 3, 4 ] [z4,z5,z6]=[2,3,4]那么经过softmax函数作用后概率分别就是: [ e 2 ( e 2 + e 3 + e 4 ) , e 3 ( e 2 + e 3 + e 4 ) , e 4 ( e 2 + e 3 + e 4 ) ] = [ 0.0903 , 0.2447 , 0.665 ] [\frac{e^2}{(e^2+e^3+e^4)},\frac{e^3}{(e^2+e^3+e^4)},\frac{e^4}{(e^2+e^3+e^4)}] = [0.0903,0.2447,0.665] [(e2+e3+e4)e2,(e2+e3+e4)e3,(e2+e3+e4)e4]=[0.0903,0.2447,0.665]如果这个样本正确的分类是第二个的话,那么计算出来的偏导就是 [ 0.0903 , 0.2447 − 1 , 0.665 ] = [ 0.0903 , − 0.7553 , 0.665 ] [0.0903,0.2447-1,0.665]=[0.0903,-0.7553,0.665] [0.0903,0.2447−1,0.665]=[0.0903,−0.7553,0.665]
正确分类数值-1 , 不正确分类数值不变
六.优缺点
-
优点
在用梯度下降法做参数更新的时候,模型学习的速度取决于两个值:一、学习率;二、偏导值。其中,学习率是我们需要设置的超参数,所以我们重点关注偏导值。从上面的式子中,我们发现,偏导值的大小取决于 [公式] 和 [公式] ,我们重点关注后者,后者的大小值反映了我们模型的错误程度,该值越大,说明模型效果越差,但是该值越大同时也会使得偏导值越大,从而模型学习速度更快。所以,使用逻辑函数得到概率,并结合交叉熵当损失函数时,在模型效果差的时候学习速度比较快,在模型效果好的时候学习速度变慢。 -
缺点
sigmoid(softmax)+cross-entropy loss 擅长于学习类间的信息,因为它采用了类间竞争机制,它只关心对于正确标签预测概率的准确性,忽略了其他非正确标签的差异,导致学习到的特征比较散。基于这个问题的优化有很多,比如对softmax进行改进,如L-Softmax、SM-Softmax、AM-Softmax等。
七.为什么逻辑回归不用MSE而用交叉熵
因为 当我们在学习逻辑回归参数的时候,会发现我们的优化目标不是凸优化,只能找到多个局部 最优值,梯度下降法很可能找不到全局最优值,虽然平方差是一个不错的损失函数,但是我 们在逻辑回归模型中会使用交叉熵损失函数。