codechef MXMN

题意：
定义一条路径的权值为经过边边权的最大值
两点u,v的权值为f(u,v)等于uv之间所有简单路径的权值的最小值
两张图G1，G2，都有n个点G1点编号为$[1,n]$,G2编号为$[n+1,n+n]$
求${\sum }_{u,v\in [1,n]}f(u,v)\ast f(u+n,v+n)$

---

显然f(u,v)为最小生成树的路径最大值
考虑在uv之间的最大权边上统计uv的答案
可以用边分治，但我不怎么会打，有点麻烦
由于是最小生成树，考虑使用kruskal重构树，对两个图都建kruskal重构树
那么u，v的答案就会在lca处统计到
在第一个重构树中枚举lca，那么这个地方的权值只对左右两子树之间的答案有贡献，现在需要求左右两子树在另一个图中的答案，我们需要一种类似左右子树合并的做法来统计。
为了保持复杂度，我们需要使用一种较浅的结构来支持合并，这就想到了点分树，对另一个kruskal重构树建点分树，那么一开始，每一个点只存有在点分树中到根的路径，接着对于枚举的lca，将左右两点分树合并，顺便维护答案，点分树合并和线段树合并类似，如果对于两边子树有同一个点，那么这个点要往下走，合并下面的子树，否则只用保留其一。
那么现在的问题在于，点分树的两个子图的同一点，如何计算答案

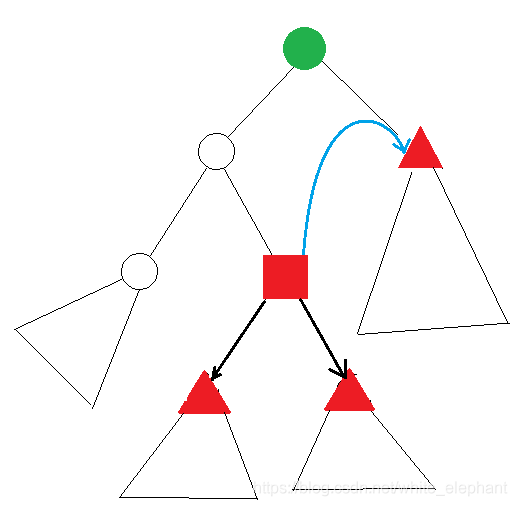
重心父亲和重心儿子可能没有祖孙后代关系
如图，两条黑边走下去的重心，两块之间的答案就是方点，答案就是个数之积乘上该重心的权值，但是对于黑边和蓝边的答案是lca就是绿点，所以在储存点分树的时候要记下那条边是往上的，那么这条边的要记录下那一块点与方点的lca权值和，蓝边与黑边的答案就是该和乘上其他两个的大小。
时间复杂度$O(n\log n)$

事实上可以对kruskal的边赋权为点权的差分，将max变为权值和，再做点分树合并，更简单点。

#include
#include
#include
#define N 200100
#define M 3800000
#define mo 998244353
using namespace std;
int s[N][3],son[N][2],n,m,top,ps[N+N],c,v[N],sz[M],sn[M][3],sm[M],Fa[N],siz[N],rt,hd,tl,que[N],fa[N],R[N],tot,ans,f[19][N+N],deep[N],lo[N+N];
bool vis[N];
struct road{int x,y,v;}a[N];
bool cmp(road a,road b){return a.v<b.v;}
int get(int x){return x==fa[x]?x:(fa[x]=get(fa[x]));}

int core(int x){
	int mn=n+n+12,p;
	for(hd=0,que[tl=1]=x;hd^tl;)
	for(int i=0,x=que[++hd],y;i<2;++i)
		if(!vis[y=son[x][i]]&&y)deep[que[++tl]=y]=deep[x]+1;
	for(;hd;--hd){
		int X=que[hd],mx=0;siz[X]=1;
		for(int i=0,y;i<2;++i)
		if(!vis[y=son[X][i]]&&y){
			siz[X]+=siz[y];
			mx=max(mx,siz[y]);
		}mx=max(mx,tl-siz[X]);
		if(mx<mn||(mn==mx&&X>n))mn=mx,p=X;
	}return p;
}
int dfs(int x){
	int C=core(x);vis[C]=1;
	if(C^x)Fa[s[C][0]=dfs(x)]=C;
	for(int i=0,y;i<2;++i)
		if(!vis[y=son[C][i]]&&y)Fa[s[C][i+1]=dfs(y)]=C;
	return C;
}
void merge(int &x,int y,int z,int w){
	if(!y||!z){x=y+z;return;}
	int A0=sn[y][0],A1=sn[y][1],A2=sn[y][2];
	int B0=sn[z][0],B1=sn[z][1],B2=sn[z][2];
	tot=(tot+(1ll*sz[A1]*sz[B2]+1ll*sz[B1]*sz[A2])%mo*v[w])%mo;
	tot=(tot+1ll*sm[A0]*(sz[B1]+sz[B2])+1ll*sm[B0]*(sz[A1]+sz[A2]))%mo;
	x=y;
	merge(sn[x][0],A0,B0,s[w][0]);
	merge(sn[x][1],A1,B1,s[w][1]);
	merge(sn[x][2],A2,B2,s[w][2]);
	sz[x]=sz[y]+sz[z];
	sm[x]=(sm[y]+sm[z])%mo;
}

void go(int x){
	f[0][++top]=v[x];ps[x]=top;
	if(son[x][0]){
		go(son[x][0]);
		f[0][++top]=v[x];
	}
	if(son[x][1]){
		go(son[x][1]);
		f[0][++top]=v[x];
	}
}
int getmx(int x,int y){
	if(x>y)swap(x,y);int l=lo[y-x+1];
	return max(f[l][x],f[l][y-(1<<l)+1]);
}
int main(){
	scanf("%d %d",&n,&m);
	for(int i=1;i<=n;++i)fa[i]=i;
	for(int i=1;i<=m;++i)scanf("%d %d %d",&a[i].x,&a[i].y,&a[i].v);
	sort(a+1,a+m+1,cmp);c=n;
	for(int i=1;i<=m;++i){
		int x=a[i].x,y=a[i].y;
		x=get(x);y=get(y);if(x==y)continue;
		++c;son[c][0]=x;son[c][1]=y;v[c]=a[i].v;
		fa[x]=fa[c]=fa[y]=c;f[0][y]=f[0][x]=c;
	}go(c);for(int i=3;i<=top;++i)lo[i]=lo[i+1>>1]+1;
	for(int j=1;j<=18;++j)for(int i=1,__=top-(1<<j)+1;i<=__;++i)f[j][i]=max(f[j-1][i],f[j-1][i+(1<<j-1)]);
	deep[c]=1;rt=dfs(c);c=0;
	for(int i=1;i<=n;++i){
		++c;sz[c]=1;int V=0;
		for(int x=i,y=Fa[i];y;x=y,y=Fa[y]){
			++c;
			for(int o=0;o<3;++o)if(x==s[y][o]){
				sn[c][o]=c-1,sz[c]=1;
				if(!o)sm[c-1]=getmx(ps[i],ps[y]);
			}
		}R[i]=c;
	}
	for(int i=1;i<=n;++i)fa[i]=i;
	for(int i=1;i<=m;++i)scanf("%d %d %d",&a[i].x,&a[i].y,&a[i].v);
	sort(a+1,a+m+1,cmp);c=n;
	for(int i=1;i<=m;++i){
		int x=a[i].x,y=a[i].y,V=a[i].v;
		x=get(x);y=get(y);if(x==y)continue;
		++c;fa[c]=fa[x]=fa[y]=c;
		tot=0;merge(R[c],R[x],R[y],rt);
		ans=(ans+1ll*tot*V)%mo;
	}printf("%d",ans);
}