课程project总结 - 蚁群算法
一、解决问题:TSP(旅行商问题)
旅行商问题是这样的:给定旅行家的起始地点和终点,要求中间必须经过所有的点,求最短路径。解决算法有蚁群算法、遗传算法、分支界定算法等。
二、蚁群算法
1、算法简述
蚁群算法是由Marco Dorigo于1992年在他的博士论文中提出的,灵感来源于蚂蚁找食物。如果一群蚂蚁现在想找食物,第一只蚂蚁的路线是完全随机的,因为没有任何条件。但是这只蚂蚁会在路上留下信息素,这样第二只蚂蚁在找路线的时候,就可以根据信息素来选择路线,有了参考。
那怎么体现选择更短的路线呢?到达食物路线更短的蚂蚁因为可以节省更多的体力,所以可以留下更多的信息素(原因是我YY出来的)。所以蚁群算法的第一个特点是正反馈。较短的路线上会留下更多的信息素,更多的信息素会吸引更多的蚂蚁走这条路,更多蚂蚁走这条路进而会提高这条路的信息素…这样就形成了一种正反馈调节。
和正反馈相对的,蚁群算法的另一种特点是多样性:蚂蚁也不一定选择信息素最多的路线,有少数蚂蚁会特立独行,选择其他路线。这样可以保证蚁群算法不至于那么死板。可以在环境发生变化之后,调节路线的信息素。
正反馈则是一种强化:它保证了较短路径的话语权,能够让优势得到强化,象征着一种权威。当然,多样性相对于正反馈就是一种挑战权威的特性。
这两个特点在自然界中都是非常重要的:如果只有多样性而没有正反馈,蚂蚁的选择就会一直杂乱无章,过于随机;而如果只有正反馈而没有多样性,整个系统就好比一潭死水,蚂蚁的选择过于僵硬而没有创新。世间万物其实都是经过了这两个条件的筛选之后形成的,能够在环境的激烈竞争中存活下来的物种,一定都是具有这两种自我调节的能力,否则都会被环境淘汰掉。
2、具体过程
蚁群算法的过程如下图所示:

对于a 图来说由于从起点A 到达食物E 只有一条路径,所以不存在选择的问题,直接就是一条路走到黑。对于b、c 图来说在A 和E 之间存在着障碍物CH,那么当第一批蚂蚁到达B 点的时候,就会随机分为两批,分别沿着BH或BC 继续朝E 点挺进,并留下相同量的信息素。由于BCD 这条路的长度明显小于BHD,所以这些蚂蚁会比较早找到E 点的食物,并沿着远路返回。而且蚂蚁在回窝的时候同样会留下信息素,所以BCD 这条路的信息素的增长速率会大于BHD,随后的蚂蚁在到达B 点的时候,就会更多地选择BCD,不过BHD 依然有少数蚂蚁选择。最后的效果就是c 图。
这么说还是比较抽象,不够具体,下面就从一个实际例子来说明:

① 如图所示,现有5个城市,先它们之间的距离矩阵如下:
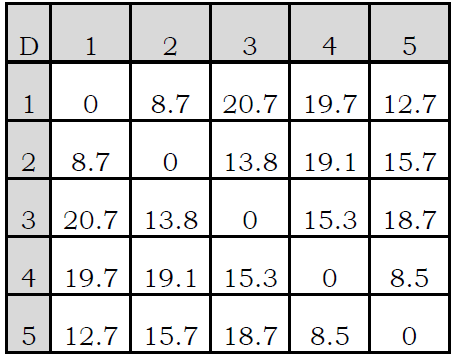
② 还是初始化,所有的信息素都为1

③ 设置参数:ALPHA = 1.0,BETA=2.0,ROU=0.5,Q=10.0
CITY_COUNT=5(前面说了城市数量为5)
ANT_COUNT=3(蚂蚁数量为城市数量的2/3)
IT_COUNT=5(迭代次数为5,规模越大迭代次数应该越多)
④ 初始化完成,下面蚂蚁开始选择路线:
从第一只蚂蚁开始,起点在第一个城市,那么它有2、3、4、5四个城市可以去,怎么选择呢?先用到一个公式,得到这四个城市被选中的概率:

其中,Tij 表示城市i 和城市j 之间的信息素,Dij 表示城市i 和城市j 之间的距离的平方,最后Pij 就是从城市i 出发到城市j 的概率了。
根据这个公式可以算出:
P12=1.0/(8.78.7)=0.013211
P13=1.0/(20.720.7)=0.002333
P14=1.0/(19.719.7)=0.002576
P15=1.0/(12.712.7)=0.006200
总的概率值Ptotal=P12+P13+P14+P15=0.02432
然后再计算到四个城市真正的概率:
p12=P12/Ptotal=54.3%
p13=P13/Ptotal=9.6%
p14=P14/Ptotal=10.6%
p15=P15/Ptotal=25.5%
结果如下图:
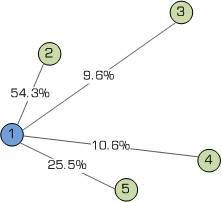
算出了概率,最后就是选择到底去哪个城市了。虽然P12 的概率最大,但是由于蚁群算法的多样性,也要保证其他城市也有机会被选中,否则,如果只选择概率最大的,就变成贪心算法了。关于怎么选择,这里用到了轮盘选择的方法,下面介绍这种方法:
⑤ 轮盘选择

现在假设蚂蚁停在D 点,蚂蚁已经走过了ABC 点,那么现在它就有EFG三种选择,现假设数据如下:
alpha=1.0 beta=2.0
DE 间信息素为2,DE 间距离为2
DF 间信息素为5,DF 间距离为2
DG 间信息素为3,DG 间距离为3
那么根据公式,EFG 被选择的概率依次是:
pro_E=2/(22)=0.5;
pro_F=5/(22)=1.25;
pro_G=3/(3*3)=0.3333;
总的概率值pro_total=pro_E+pro_F+pro_G=0.5+1.25+0.333=2.083
然后得到真正被选择的概率:
pE=pro_E/pro_total=0.5/2.083=24%
pF=pro_F/pro_total=1.25/2.083=60%
pG=pro_G/pro_total=0.333/2.083=16%
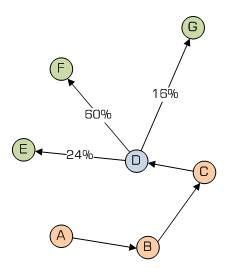
然后就是轮盘选择:首先在[0, 1]之间选择一个随机浮点数,然后先减去pE,如果得到的值小于等于0,就选择E 作为下一个点,否则,就接着减去pF,如果还大于0,再减去pG…
假设现在得到的随机数是0.9,根据上面的算法,最后得到的下一个点就是G 点(0.9-0.24=0.66, 0.66-0.6=0.06, 0.06-0.16=-0.1<0)。画一个轮盘也可以看得出来:
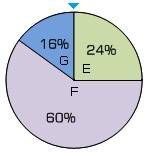
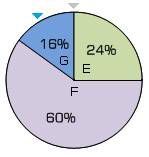
左图的蓝色指针向逆时针旋转90%,到达G 的部分,所以最后选择的是G。这种方式才真正体现了轮盘算法的精髓。
从上面的轮盘也可以看出:F 点选中的概率是最大的,只要随机数在区间(0.24, 0.6]都可以;E 次之,G 概率最小,但都是有一定几率的。
⑥ 前面用轮盘算法,选择了第一只蚂蚁的第二个到达的城市,后面选择的城市同样是用到这种方法。现在假设第一只蚂蚁选择的路径如下:
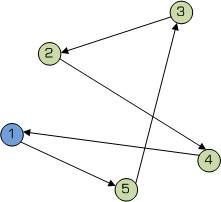
1->5->3->2->4,路径长为84。
⑦ 第二、第三只蚂蚁重复第一只蚂蚁的过程,现在假设他们的路径为:
第2 只蚂蚁走得路径是1->2->3->5->4->1 路径长度是:69.4
第3 只蚂蚁走得路径是1->5->4->2->3->1 路径长度是:74.8
⑧ 所有的蚂蚁走完之后,就可以更新环境信息素了。信息素的变化受到两个因素影响:首先是环境使信息素自然减少。前面说到ROU=0.5,也就是挥发系数为0.5,那么新信息素=(1-ROU)*原信息素,故新信息素是原来的一半:

还有第二个因素:每只蚂蚁在走过的路径都会留下一些信息素,留下的量
由下面的公式控制:
蚂蚁在路径上留下的信息素=Q/L
其中L 是蚂蚁走过的路径长度,Q 是信息素总量。这里设置的Q=10.0。
故第一只蚂蚁在它走过的路径留下的信息素量为:10.0/84=0.119。
第一只蚂蚁走过的路径为1->5->3->2->4->1,所以1-5、3-5、2-3、2-4、1-4之间的路径都要加上0.119,如下:


第二、第三只蚂蚁也是用这种方法,更新环境信息素。
⑨ 进行第二次循环,如果找到了更短的路径,就更新最短路径和长度
⑩ 输出最好的结果
以上就是蚁群算法工作的整个流程,下面介绍整个代码的实现:
3、代码实现
(1)相关参数
const double ALPHA = 1.0; // 启发因子,信息素的重要程度
const double BETA = 2.0; // 期望因子,城市间距离的重要程度
const double ROU = 0.5; // 信息素挥发系数
int num_ant; // 蚂蚁数量,读入数据后更新,设定为城市数量的2/3
int num_city; // 城市数量,读入数据后更新
const int num_it = 5000; // 迭代次数
const double DBQ = 100.0; // 总的信息素
const double DB_MAX = 10e9; // 一个标志数
double Trial[110][110]; // 城市之间的信息素数量总和
double Distance[110][110]; // 城市之间的距离
const int start_city = 1; // 起点城市
double x_p[110]; // 城市的横坐标
double y_p[110]; // 城市的纵坐标
注:蚂蚁数量和城市数量是在读取储存坐标或者距离信息的文本之后才确定的。
(2)基本函数
① 读取城市信息
储存城市信息有两种方式:一种是用矩阵直接存每两个城市之间的距离,还有一种是储存每一个城市的坐标,距离自己计算。
// 从一个文件中读取城市的坐标
void read_point(char *c)
{
ifstream i(c);
i >> num_city;
int j = 1;
while (!i.eof()){
i >> x_p[j] >> y_p[j];
j++;
}
i.close();
num_ant = int (2.0/3*num_city);
caldis();
}
// 从一个文件中读取城市之间的距离
void read_distance(char *c)
{
ifstream i(c);
i >> num_city;
int j = 1, k = 1;
while (!i.eof()){
i >> Distance[j][k];
if (++k > num_city){
k = 1;
j++;
}
}
i.close();
num_ant = int (2.0/3*num_city);
}
② 产生随机数
刚刚说到的轮盘算法,就用到了随机数。不过,即使用了srand(time(0)),试图让每次执行算法产生的随机数都不同,如果时间相隔不足一秒,产生的随机数依然是差不多的。
所以,一种思路是在执行完每一次轮盘选择之后,都执行windows.h库里的函数Sleep(1000),然后再执行srand(time(0))这样就可以保证每次产生的随机数都不相同了。但是,这样也会导致程序执行时间变长…
总之,计算机产生的随机都是伪随机,都不是真正的随机。
// 产生[l, h]之间的随机整数
int rnd(int l, int h)
{
return l + rand() % (h - l+1);
}
// 生成[l, h]之间的随机浮点数
double rnd(double l, double h)
{
double tmp = rand()/(double(RAND_MAX)+1.0);
return l+tmp*(h-l);
}
(3)蚂蚁类
蚂蚁类应该具有下面的行为:
① 初始化,从起点城市出发
② 选择下一个城市
③ 移动到下一个城市
④ 如果所有城市都去过了,回到起点城市,到第五步,否则回到第二步
⑤ 计算走过的路径长度
接下来看看怎么实现:
class Ant
{
public:
bool is_visit[110]; // 用来判断第n个点是否走过
int path[110]; // 记录经过的城市
double len; // 记录走过的路径长度
int current_city; // 当前所在的城市
int num_visit_city; // 走过的城市数
Ant();
void init_ant(); // 对蚁类变量的初始化
int choose_next_city(); // 选择下一个到达的城市
void move_cal(); // 移动到下一个被选择的城市,并更新路径
void search(); // 这只蚂蚁执行一次遍历,这个函数也是TSP类要调用的函数
void print(); // 输出这只蚂蚁走过的路径以及长度
void test_ant(char *add); // 专门针对蚂蚁类的测试
};
Ant::Ant()
{
}
void Ant::init_ant()
{
for (int i = 1; i <= num_city; i++){
is_visit[i] = false;
}
current_city = start_city;
is_visit[current_city] = true;
len = 0;
path[1] = current_city;
num_visit_city = 1;
}
int Ant::choose_next_city()
{
int select_city = -1; // 首先设定返回值为-1,假定选择下一个城市失败
double totalp = 0; // 记录各个城市被选中的概率之和
double *p = new double[110]; // 记录各个城市被选中的概率
// int p_pos = 0; // 记录有多少个城市还没被选中
// 首先用公式算出没去过的城市被选中的概率
for (int i = 1; i <= num_city; i++){
p[i] = 0; // 注意!一定要赋初值为0
if (is_visit[i]) continue;
// 用到公式 P = T^ALPHA/(D^BETA)
p[i] = pow(Trial[current_city][i]*1.0, ALPHA)/pow(Distance[current_city][i]*1.0, BETA);
totalp += p[i];
}
// 然后算出真正被选中的概率,由于取随机数的函数可以选择上下界,所以这一步可以不用
/*for (int i = 1; i <= num_city; i++){
p[i] /= totalp;
}*/
// 用轮盘选择的方法选出下一个城市
if (totalp > 0.0){
double tmp_p = rnd(0.0, totalp); // 选取被减的概率
for (int i = 1; i <= num_city; i++){
if (is_visit[i]) continue;
tmp_p -= p[i];
if (tmp_p <= 0){ // 直到tmp_p小于等于0
select_city = i;
break;
}
}
}
// 注意!由于迭代次数可能会比较大,信息素会降得很厉害,最后可能小到double都不能表示
// 导致概率总和为0,因为概率计算公式的分母就是信息素
// 这个时候就把第一个没去过的城市作为下一个城市
if (select_city == -1){
for (int i = 1; i <= num_city; i++){
if (!is_visit[i]) {
select_city = i;
break;
}
}
}
delete []p;
return select_city;
}
void Ant::move_cal()
{
int next_city = choose_next_city(); // 得到下一个城市
if (next_city == -1) return ;
is_visit[next_city] = true; // 将下一个城市的状态设定为"走过"
len += Distance[current_city][next_city]; // 路径长度增加
path[++num_visit_city] = next_city; // 走过的城市数增加
current_city = next_city; // 下一个城市成为当前的城市
if (num_visit_city == num_city) len += Distance[current_city][start_city]; // 最后还要加上到起点城市的距离
}
void Ant::search()
{
init_ant();
while (num_visit_city < num_city){
//cout << num_visit_city << endl;
move_cal();
}
}
(4)TSP类
前面实现的蚂蚁类只是单个个体的行为,蚁群算法是多个蚂蚁的行为,还有更新环境信息素、输出最后结果,这些工作都要交给TSP 类来做:
① 初始化信息素、计算城市之间的距离(如果输入的是城市的坐标)
② 管理多个蚂蚁,让这些蚂蚁执行遍历,执行迭代次数次
③ 最后一只蚂蚁完成遍历之后,更新信息素,并保留最短路径和长度
④ 输出最后的结果
class TSP
{
public:
Ant ant_ary[110]; // 管理的蚂蚁数组,其实真正的大小是num_ant
Ant best_ant; // 路径最短的那只蚂蚁
int bestpos; // 最优蚂蚁的下标
void init(); // 初始化信息素等变量
TSP(char *c); // 构造函数,读入城市信息
void update_Trial(); // 更新信息素
void update_Trial_V2(int); // 改进后的更新信息素的方法
void search(); // 执行所有蚂蚁的遍历操作
void print(); // 把最后的结果输出
void print_Trial(); // 输出信息素
};
TSP::TSP(char *c)
{
//read_point(c);
read_distance(c);
init();
}
void TSP::init()
{
// 首先将最优路径的长度设置为一个很大的值
best_ant.len = DB_MAX;
// 初始化环境信息素
for (int i = 1; i <= num_city; i++){
for (int j = 1; j <= num_city; j++) Trial[i][j] = DBQ;
}
}
void TSP::update_Trial()
{
// 首先环境因素至信息素自然蒸发一部分
for (int i = 1; i <= num_city; i++){
for (int j = 1; j <= num_city; j++){
Trial[i][j] = (1.0-ROU)*Trial[i][j];
}
}
// 然后每只蚂蚁在经过的路上都会留下信息素,量用到公式Q/L,还要注意信息素的增加是双向的
for (int i = 1; i <= num_ant; i++){
for (int j = 1; j <= num_city; j++){
if (j == num_city){
Trial[ant_ary[i].path[j]][start_city] += 1.0*DBQ/ant_ary[i].len;
Trial[start_city][ant_ary[i].path[j]] += 1.0*DBQ/ant_ary[i].len;
}
else {
Trial[ant_ary[i].path[j]][ant_ary[i].path[j+1]] += 1.0*DBQ/ant_ary[i].len;
Trial[ant_ary[i].path[j+1]][ant_ary[i].path[j]] += 1.0*DBQ/ant_ary[i].len;
}
}
}
}
void TSP::update_Trial_V2(int pos)
{
// 首先环境因素至信息素自然蒸发一部分
for (int i = 1; i <= num_city; i++){
for (int j = 1; j <= num_city; j++){
Trial[i][j] = (1.0-ROU)*Trial[i][j];
}
}
// 然后只有最优的蚂蚁才能够修改环境信息素
for (int j = 1; j <= num_city; j++){
if (j == num_city){
Trial[ant_ary[pos].path[j]][start_city] += 1.0*DBQ/ant_ary[pos].len;
Trial[start_city][ant_ary[pos].path[j]] += 1.0*DBQ/ant_ary[pos].len;
}
else {
Trial[ant_ary[pos].path[j]][ant_ary[pos].path[j+1]] += 1.0*DBQ/ant_ary[pos].len;
Trial[ant_ary[pos].path[j+1]][ant_ary[pos].path[j]] += 1.0*DBQ/ant_ary[pos].len;
}
}
}
void TSP::search()
{
for (int i = 0; i < num_it; i++){
// 首先每只蚂蚁都执行一次遍历
for (int j = 1; j <= num_ant; j++){
ant_ary[j].search();
}
// 然后看最优蚂蚁是否需要更新
for (int j = 1; j <= num_ant; j++){
if (ant_ary[j].len < best_ant.len){
best_ant = ant_ary[j];
bestpos = j;
}
}
// 所有蚂蚁都遍历完之后,更新环境信息素
update_Trial();
//update_Trial_V2(bestpos);
// 最后输出当前循环之后的最优路径
printf("第%d次迭代后最优路径长度:%.0f\n", i+1, best_ant.len);
}
}
三、算法优化:MMAS(最大最小蚁群算法)
MMAS由Thomas Stutzle和Holger H.Hoos在2000年提出:
改进主要体现在下面4点:
(1) 在每次循环之后,只有最优的蚂蚁可以进行信息素更新。最优解可以是迭代最优解,也可以是全局最优解,也可以是两者的混合策略,一般使用全局最优解。更新公式如下:

f(Sbest)是最优蚂蚁走过的路径长度。
ρ是信息素残留系数。
全局最优解:就是到目前为止找到的最优解。
迭代最优解:就是本次循环找到的最优解。
(2) 环境信息素有最大、最小值的限制,每次更新完信息素后要进行检查,如果超过限制要进行调整。最大最小信息素计算公式如下:

f 是全局最优解蚂蚁的路径长度。
ρ是信息素残留系数,注意是残留系数,不是挥发系数!!!
avg=n/2其中 n是城市数量。
Pbest=0.05或者0.005。Pbest文档中的意思好像是蚂蚁一次搜索找到最优解的概率(本人英文不佳,看原版论文里的意思应该是这个)。
另外要注意的是信息素的最大最小值不是固定的,如果有更好的解产生,则要重新进行计算。
(3)环境信息素初始化为Tmax,算法最开始的时候没有全局最优解,可以用贪心算法生成一个解作为最优解(贪心算法就是蚂蚁总是往距离它最近的城市移动)。
(4)信息素平滑策略,在求解规模比较大的问题或者迭代次数比较多的时候,当算法陷入停滞的时候,可以使用下面方法重新设置环境信息素。公式如下:
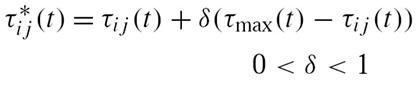
四、代码和数据下载地址
城市数据
代码