2017蓝桥杯整理

迷宫

1.简单深搜

#include
#include
using namespace std;
string data[10];
int ans;
int vis[10][10];//标记
bool solve(int i,int j){
 if(i<0||i>9||j<0||j>9)
 return true;
 if(vis[i][j]==1) return false;
 vis[i][j]=1;
 switch(data[i][j]){
  case 'U':return solve(i-1,j);
  case 'D':return solve(i+1,j);
  case 'L':return solve(i,j-1);
  case 'R':return solve(i,j+1);
  default:return false;
 }
 }
 int main(){
  data[0]="UDDLUULRUL";
  data[1]="UURLLLRRRU";
  data[2]="RRUURLDLRD";
  data[3]="RUDDDDUUUU";
  data[4]="URUDLLRRUU";
  data[5]="DURLRLDLRL";
  data[6]="ULLURLLRDU";
  data[7]="RDLULLRDDD";
  data[8]="UUDDUDUDLL";
  data[9]="ULRDLUURRR";
  for(int i=0;i<10;i++)
  for(int j=0;j<10;j++){ 
  memset(vis,0,sizeof(vis)); 
  bool res=solve(i,j);
  if(res) ans++;
  }
  cout<<ans<<endl;
  return 0;
 }

跳蚱蜢

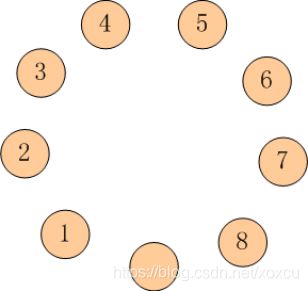
有9只盘子，排成1个圆圈。
其中8只盘子内装着8只蚱蜢，有一个是空盘。
我们把这些蚱蜢顺时针编号为 1~8
每只蚱蜢都可以跳到相邻的空盘中，
也可以再用点力，越过一个相邻的蚱蜢跳到空盘中。
请你计算一下，如果要使得蚱蜢们的队形改为按照逆时针排列，
并且保持空盘的位置不变（也就是1-8换位，2-7换位,…），至少要经过多少次跳跃？
注意：要求提交的是一个整数，请不要填写任何多余内容或说明文字。

1.宽搜
2.用数组模拟状态

#include//宽搜 
#include
#include
#include
#include
using namespace std;
char *start="012345678";
char *target="087654321";
struct StateAndLevel{
 char *state;//当前状态 
 int level;
 int pos0;//零的位置 
 StateAndLevel(char *_state,int _level,int _pos0):state(_state),level(_level),pos0(_pos0){}  
}; 
struct cmp{
 bool operator()(char* a,char* b){ 
 return strcmp(a,b)<0;}
};
queue<StateAndLevel> q;
set<char*,cmp>allState;
void swap(char *s,int a,int b){
 char t=s[a];
 s[a]=s[b];
 s[b]=t;
}
void addNei(char *state,int pos,int new_Pos,int le){
 char *new_state=(char*)malloc(9*sizeof(char));
  strcpy(new_state,state);
  //交换
  swap(new_state,pos,new_Pos);
  if(allState.find(new_state)==allState.end()){ 
  allState.insert(new_state);
  q.push(StateAndLevel(new_state,le+1,new_Pos));
  } 
}
int main(){
 q.push(StateAndLevel(start,0,0));
 while(!q.empty()){
  StateAndLevel sal=q.front();
  char *state=sal.state;
  int le=sal.level;
  if(strcmp(state,target)==0){//已达目标状态 
   cout<<le<<endl;
   return 0;
  } 
  int pos0=sal.pos0; 
  allState.insert(state);
  //添加邻居左一 
  int new_pos=(pos0-1+9)%9;
  addNei(state,pos0,new_pos,le);
  //添加左二 
   new_pos=(pos0-2+9)%9;
  addNei(state,pos0,new_pos,le);
  //添加右一 
   new_pos=(pos0+1+9)%9;
        addNei(state,pos0,new_pos,le);
        //添加右二 
         new_pos=(pos0+2+9)%9;
         addNei(state,pos0,new_pos,le);
  q.pop(); 
 }
 return 0;
}

魔方状态

这道题不会

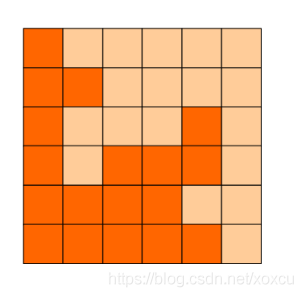
方格分割

6x6的方格，沿着格子的边线剪开成两部分。
要求这两部分的形状完全相同。
如图4-1,4-2,4-3：就是可行的分割法。
试计算：
包括这3种分法在内，一共有多少种不同的分割方法。
注意：旋转对称的属于同一种分割法。
请提交该整数，不要填写任何多余的内容或说明文字。

#include
using namespace std;
int ans;
int dire[][2]={{-1,0},{1,0},{0,-1},{0,1}};
int vis[7][7];
void dfs(int x,int y){
 if(x==0||y==0||x==6||y==6)
 {
  ans++;
  return;
 }
 vis[x][y]=1;
 vis[6-x][6-y]=1;
 for(int k=0;k<4;k++){
  int nx=x+dire[k][0];
  int ny=y+dire[k][1];
  if(nx<0||nx>6||ny<0||ny>6) continue;
  if(!vis[nx][ny]){
   dfs(nx,ny);
  }
 }
 vis[x][y]=0;
 vis[6-x][6-y]=0;
}
int main(){
 dfs(3,3);
 cout<<ans/4;
 return 0;
}

正则问题

1.二分

#include
#include
using namespace std;
char s[100];
int len;
int pos;
//求出当前字符串，自当前下标到结束能匹配的字符串长度 
int f(){
 int ans=0;
 int tmp=0;//用于保存连续的x数量 
 int m=0;
 while(pos<len){ 
 if(s[pos]=='('){
  pos++;
  tmp+=f();//等待后面的结果并累加到ans 
 }
  else if(s[pos]=='x'){
   pos++;
   tmp++;
  }
  else if(s[pos]=='|'){
   pos++;
   m=max(m,tmp);
   tmp=0;
  } 
  else if(s[pos]==')'){
   pos++;
   m=max(m,tmp);
   break;
  }
 }
 m=max(m,tmp);
 return m; 
}
int main(){
 cin>>s;
 len=strlen(s);
 int ans=f();
 cout<<ans<<endl;
 return 0;
}

分巧克力

儿童节那天有K位小朋友到小明家做客。小明拿出了珍藏的巧克力招待小朋友们。
小明一共有N块巧克力，其中第i块是Hi x Wi的方格组成的长方形。
为了公平起见，小明需要从这 N 块巧克力中切出K块巧克力分给小朋友们。切出的巧克力需要满足：
1. 形状是正方形，边长是整数
2. 大小相同
例如一块6x5的巧克力可以切出6块2x2的巧克力或者2块3x3的巧克力。
当然小朋友们都希望得到的巧克力尽可能大，你能帮小Hi计算出最大的边长是多少么？

1.二分查找

#include//枚举 优化 
using namespace std;
int main(){
 int n,k;
 int h[100000];//长 
 int w[100000];//宽  
 cin>>n>>k;
 for(int i=0;i<n;i++){
  cin>>h[i]>>w[i];
 }
 //int len=100000;
 int r=100001;
 int l=1;
 int ans=0;
 while(l<=r){
  int mid=(l+r)/2;
  int cnt=0;
 //for(;len>=1;len--){
  //int cnt=0;
  for(int i=0;i<n;i++){
   cnt+=(h[i]/mid)*(w[i]/mid);
  }
  if(cnt>=k) {l=mid+1;ans=mid;} 
  else r=mid-1;
 }
 cout<<ans<<endl;
 return 0;
} 

油漆面积

X星球的一批考古机器人正在一片废墟上考古。
该区域的地面坚硬如石、平整如镜。
管理人员为方便，建立了标准的直角坐标系。
每个机器人都各有特长、身怀绝技。它们感兴趣的内容也不相同。
经过各种测量，每个机器人都会报告一个或多个矩形区域，作为优先考古的区域。
矩形的表示格式为(x1,y1,x2,y2)，代表矩形的两个对角点坐标。
为了醒目，总部要求对所有机器人选中的矩形区域涂黄色油漆。
小明并不需要当油漆工，只是他需要计算一下，一共要耗费多少油漆。
其实这也不难，只要算出所有矩形覆盖的区域一共有多大面积就可以了。
注意，各个矩形间可能重叠。
本题的输入为若干矩形，要求输出其覆盖的总面积。
1.线段树问题
2.现只会枚举

#include
using namespace std;
int n,sum;
bool p[10005][10005];
void paint(int x1,int y1,int x2,int y2){
 for(int i=x1;i<x2;i++)
 for(int j=y1;j<y2;j++)
 p[i][j]=1;
}
int main(){
 cin>>n;
 for(int i=0;i<n;i++){
  int x1,y1,x2,y2;
  cin>>x1>>y1>>x2>>y2;
  paint(x1,y1,x2,y2);
 }
 for(int i=0;i<10005;i++)
 for(int j=0;j<10005;j++)
 if(p[i][j]==1) sum++;
    cout<<sum<<endl;
}