PRML笔记（一）

1 Introduction

本章主要讲解的是三大理论的一些基本概念知识，这三大理论分别为：probability theory，decision theory 以及 information theory。

1.1 Example: Polynomial Curve Fitting

本章刚开始便引入了一个“polynomial curve fitting”的regression problem。在这个拟合问题中，所要拟合的函数是sin($2\pi x$)，在生成数据时，本书的方法是：首先从(0,1)区间上等间距地得到input data x，然后通过sin($2\pi x$)计算得到一个数值，并用该数值与一个Gaussian noise相加，遂得到最终的结果。更为详细的过程见《PRML附录笔记》，其示意图如下所示：

那么为何要这样构造？首先，当我们对于数据的生成过程了如指掌之后，我们就很容易对一些learnable models进行比较，分析其performance。
为什么要加上噪声？因为这种方式正符合一般数据的生成过程：确定的函数+随机噪声。在正常数据的生成与获取过程中，我们一般都会遇到两种噪声：一是由随机过程引起的噪声（例如放射性物质的衰减）；二是由于该数据本身有某些unobserved的部分，这些部分的variability所带来的noise。
我们的目的在于：挖掘training data set中的regularity，并在遇到新的input data时，可以对output data进行更为准确的预测。
我们将如何应对数据本身带来的noise？在probability theory这一节中，作者将对这样的noise进行量化。而在decision theory中，作者将讲述如何利用这个probabilistic representation的方法，在某种特定的criterion下，进行最优决策。

本处将采用多项式来对生成的数据进行拟合：
$$y(x,\mathbf{w})=w_0+w_{1}x+w_2{x}^2+\cdots +w_M{x}^M=\sum _{j=0}^M{w}_j{x}^j(1.1)$$
其中多项式系数通过vector $\mathbf{w}$ 来进行表示。虽然该式是关于x的非线性函数，但它是关于系数 $\mathbf{w}$ 的线性函数，因此被称为“linear model”。而linear model将在第3和4章重点讨论。
我们当前的目标在于寻找最合适的系数 $\mathbf{w}$，那么我们应该如何去做？首先我们需要意识到的一点是， 我们希望我们构造的多项式函数能尽可能地拟合我们所得到的数据。因此，我们可以通过minimize error function的方式，对 $y(x,\mathbf{w})$ 与在training set中真实的target value t之间的差异进行衡量。
一种选取error function的的方式是平方误差和（sum of the squares of the errors）:
$$E(\mathbf{w})=\frac{1}{2}\sum _{n=1}^N\{y(x_n,\mathbf{w})-t_n{\}}^2(1.2)$$
由该函数的特性可知，当且仅当该函数穿过training set中的所有data points之后，该式才等于0，否则该式大于0：

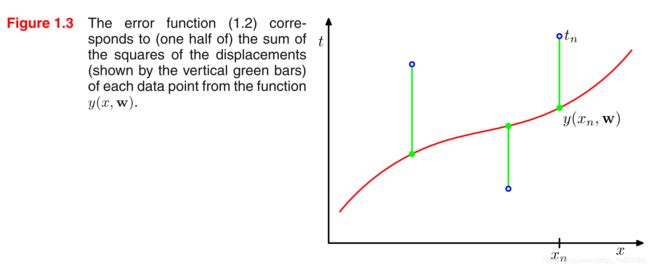
当我们选定了要用多项式函数去拟合training data之后，我们有两件事情同时需要去做：一是选择合适的系数；二是确定多项式的次数。
由于该error function是二次函数，因此其关于系数的derivative是linear function，所以该error function的最小值存在唯一解，我们将该解所对应的系数标记为 ${\mathbf{w}}^{\ast }$。
至于该多项式的order的选取，我们需要通过“model selection”这一方法进行。下图所示的，为在不同order值选取后，该多项式函数对于training data的拟合情况：

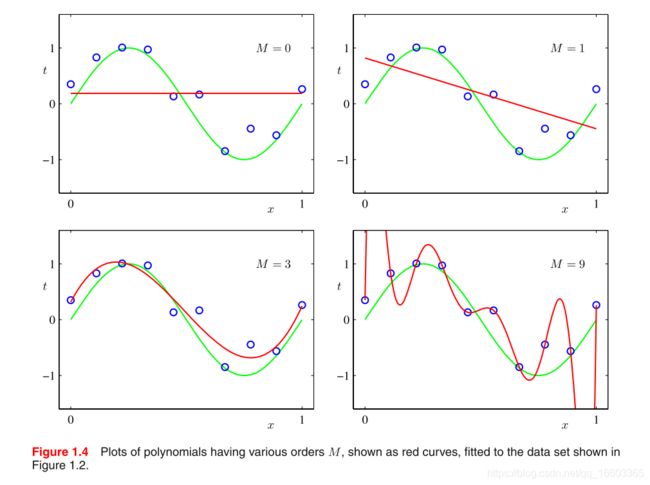
过小的order在training set上表现出较差的performance，过大的order会和真实的函数 sin($2\pi x$)之间相差甚远，导致overfitting的发生。
有时候我们希望将不同来源的error放在同一个scale下（以单个data point为scale）进行比较，此时我们可以采用root-mean-square error：
$$E_{RMS}=\sqrt{\frac{2E({\mathbf{w}}^{\ast })}{N}}$$
当然，具体而言，我们的training set和testing set中数据点的个数往往是不同的。那么如果我们想要将training set 和 testing set下模型的error放在一起比较，那么我们首先需要通过RMS error进行处理。
我们对不同order下该多项式函数模型在training和testing set上的error进行计算，并绘制成图，如下所示：

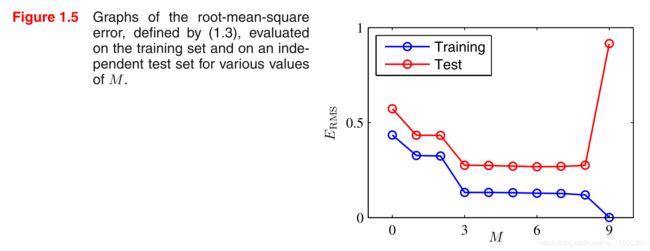
该结果与之前分析的相符合，当order过小的时候，model在两个数据集上的表现都不好；当order过大的时候，尽管model在training set上的表现较好，但在testing set上的表现极差。
有人可能会有这样的疑问：高次的多项式中不是本应包含低次的多项式吗？是这样的，然后由于高次多项式本身的灵活性非常大，导致它不仅拟合了数据中sin($2\pi x$) 的部分，也同样拟合了noise的部分。
那么，当我们给定了model，即确定了该model的complexity之后，如果我们改变dataset的size，之前出现overfitting的model的performance又是如何呢？如下图所示：

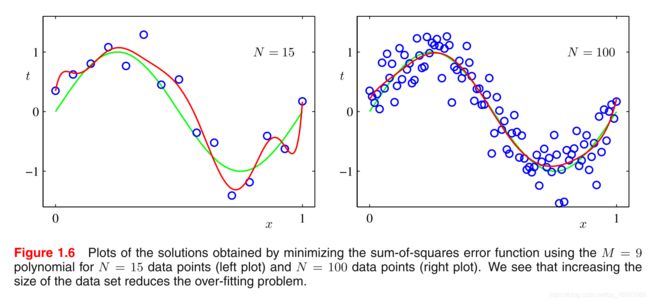
我们可以看到，当数据量增大之后，模型over-fitting的问题减轻了。
然而很多时候，我们的dataset中的数据量是有限的，然而我们仍然希望通过某一种较为复杂的函数，对这些数据进行拟合，那么我们需要如何去做？
一种控制过拟合问题发生的方法是“regularization”，它通过在(1.2)式上加入惩罚项的方式，希望模型的参数尽量不要过大，一种较为简单形式的error function如下：
$$E(\mathbf{w})=\frac{1}{2}\sum _{n=1}^N\{y(x_n,\mathbf{w})-t_n{\}}^2+\frac{\lambda }{2}||\mathbf{w}|{|}^2(1.4)$$
其中有 $||\mathbf{w}|{|}^2=w_0^2+w_1^0+\cdots +w_M^2$。其中的$\lambda$用于控制error和penalty之间的权重。
在使用regularization方法之后，原先overfitting的model在数据集上的表现如下所示：

可见，一个合适的 $\lambda$ 参数，会让原模型overfitting的问题大大减轻，然而过大的 $\lambda$ 会使得model的performance欠佳。

1.2 Probability Theory

由于测量方法所造成的noise，或是由于数据集有限的原因，我们的数据中存在许多的uncertainty。而本节内容，将用一种统一的框架，对这些uncertainty进行处理。
对于probability theory，我们首先要知道的是两个最基本的公式，即sum rule 和 product rule：
$$\begin{gathered} \mathbf{s}\mathbf{u}\mathbf{m}\mathbf{r}\mathbf{u}\mathbf{l}\mathbf{e}p(X)=\sum _{Y}p(X,Y)(1.10) \\ \mathbf{p}\mathbf{r}\mathbf{o}\mathbf{d}\mathbf{u}\mathbf{c}\mathbf{t}\mathbf{r}\mathbf{u}\mathbf{l}\mathbf{e}p(X,Y)=p(Y|X)p(X)(1.11) \end{gathered}$$
根据式(1.11)，以及对称特性：p(X,Y)=p(Y,X)，我们可以得到Bayes’ theorem：
$$p(Y|X)=\frac{p(X|Y)p(Y)}{p(X)}(1.12)$$
再利用sum rule，我们可以得到Bayes’ theorem的分母为：
$$p(X)=\sum _{Y}p(X|Y)p(Y)(1.13)$$
其中，作者还对prior probability以及posterior probability进行了解释：对于变量Y的prior probability，实际上是在我们还没有对X进行观测时，对Y发生的概率所进行的估计。而对于变量Y的posterior probability，实际上是在对X进行观测，并得知X具体取值的前提下，我们对prior的一种修正。
此外，关于两个变量相互独立的定义：p(X,Y)=p(X)p(Y)。并且，运用product rule可以得知，在两个随机变量相互独立的前提下，有p(Y|X)=p(Y)。

1.2.1 Probability densities

• 之前所有的问题都是关于离散变量的，当将关注点转向连续型变量之后，我们需要对real-valued random variable的概率分布进行分析：
  • 假设real-valued variable x落在区间 $(x,x+\delta x)$ 内的概率为 $p(x)\delta x$ （当 $\delta x\to$ 0时），则此时p(x)被称为概率密度。因此，当x落在(a,b)区间内时，其概率为：
    $$p(x\in (a,b))={\int }_a^{b}p(x)\text{d}x(1.24)$$
    又由于概率的非负性以及x在实数范围取值的规定，所以可得：
    $$\begin{gathered} p(x)\ge 0(1.25) \\ {\int }_{-\infty }^{\infty }p(x)\text{d}x=1(1.26) \end{gathered}$$
• 我们需要注意的一点是问题是：
  • 设有一个在variables之间的non-linear transformation x=g(y)，那么，对于确定性的函数来说，f(x)可以表示成：$f(y)=f(g(y))$。由此，我们也可以根据transformation function g，在概率密度函数 $p_x(x)$ 和 $p_y(y)$ 之间找到对应关系。假设有observations落在了($x,x+\delta x$)这个区间内，那么在经过transformation g之后，必然是存在另一个对应的区间($y,y+\delta y$)，在这两个区间内，对应的随机变量的取值概率近似相等，即：$p_x(x)\delta x\simeq p_y(y)\delta y$，因此便有：
    $$\begin{gathered} p_y(y)=p_x(x)\left|\frac{dx}{dy}\right| \\ =p_x(g(y))\left|g\prime (y)\right|(1.27) \end{gathered}$$
    上述文字中，加粗的部分是我要着重说明的，因为书上并没有点透到这一步。
    从另一个角度我们也可以进行理解：这里面要进行的non-linear transformation实际上是要在累积分布函数(CDF)上进行，因此转换到概率密度函数时，必然存在一个求一阶导的过程，通过该过程中所要使用的求导链式法则，我们就可以得到上式。
    那么通过式(1.27)，我们能得到什么信息呢？如果两个随机变量之间存在非线性关系，那么这两个随机变量取到概率密度最大值时的变量值（记为：$x^{\ast },y^{\ast }$），一般不满足关系：$x^{\ast }=g(y^{\ast })$。所以说，概率密度最大值，其实际上与我们所选取的变量有关。
    x落在区间($-\infty ,z$)之间的概率为：
    $$P(z)={\int }_{-\infty }^{z}p(x)dx(1.28)$$
    其中P(z)就是被称为cumulative distribution function(CDF)的函数，该函数满足：$P^{\prime }(x)=p(x)$。
    而如果我们有一连串的continuous variables：$x_1,\dots ,x_D$, 统一用vector $\mathbf{x}$来表示，那么我们可以定义联合概率密度函数：$p(\mathbf{x})=p(x_1,\dots ,x_D)$, 且对于落在 $\delta \mathbf{x}$ 大小的区间内的vector $\mathbf{x}$来说，生成该vector的概率为 $p(\mathbf{x})\delta \mathbf{x}$, 此时该多元概率密度函数应当满足：
    $$\begin{gathered} p(\mathbf{x})\ge 0(1.29) \\ \int p(\mathbf{x})\text{d}\mathbf{x}=1(1.30) \end{gathered}$$
    其中式(1.30)中的积分将遍历 $\mathbf{x}$ 所在的空间，并进行积分。
    此外，sum rule以及product rule也可以在continuous variable上进行apply：
    $$\begin{gathered} p(x)=\int p(x,y)\text{d}y(1.31) \\ p(x,y)=p(y|x)p(x)(1.32) \end{gathered}$$

1.2.2 Expectations and covariances

Probability的一个作用是计算得到某一个特定函数的weighted sum。函数f(x)在概率p(x)下的weighted sum称为该函数的期望，记作 $\mathbb{E}[f]$，在离散随机分布的情况下有：
$$\mathbb{E}[f]=\sum _{x}p(x)f(x)(1.33)$$
在连续随机分布下，p(x)将选择为该概率分布的概率密度函数：
$$\mathbb{E}[f]=\int p(x)f(x)\text{d}x(1.34)$$

假如我们只有从某一个概率分布（无论是离散还是连续的）中sample出来的N个点，我们该如何估计函数f(x)在p(x)下的期望呢？此时的计算公式非常简单：
$$\mathbb{E}[f]\simeq \frac{1}{N}\sum _{n=1}^{N}f(x_n)(1.35)$$

假设我们的函数f具有两个变量x,y, 为了单纯求f(x,y)关于p(x)的期望，我们这样表示：
$${\mathbb{E}}_x[f(x,y)](1.36)$$
此时，式(1.36)就仅仅是关于y的函数了。

而假设我们所研究的函数f需要关于分布p(x|y)进行期望求得时，我们可以将该期望表示如下：
$${\mathbb{E}}_x[f|y]=\sum _{x}p(x|y)f(x)(1.37)$$
该期望被称为“条件期望”（对于连续条件分布下的公式同样可以类比得出）。

关于f(x)的方差定义如下：
$$\text{var}[f]=\mathbb{E}\left[(f(x)-\mathbb{E}[f(x)]{)}^2\right](1.38)$$
该量用以描述f(x)相对于其期望 $\mathbb{E}[f(x)]$ 的variability。
对于上述期望公式，我们可以进一步推导如下：
$$\text{var}[f]=\mathbb{E}[f(x{)}^2]-\mathbb{E}[f(x){]}^2(1.39)$$

特别的，当f(x)=x时，有：
$$\text{var}[x]=\mathbb{E}[x^2]-\mathbb{E}[x{]}^2(1.40)$$

对于两个随机变量x和y，二者之间的covariance为：
$$\begin{gathered} \text{cov}[x,y]={\mathbb{E}}_{x,y}[\{x-\mathbb{E}[x]\}\{y-\mathbb{E}[y]\}] \\ ={\mathbb{E}}_{x,y}[xy]-\mathbb{E}[x]\mathbb{E}[y](1.41) \end{gathered}$$
而对于两个随机向量 $\mathbf{x}$ 和 $\mathbf{y}$，有：
$$\begin{gathered} \text{cov}[\mathbf{x},\mathbf{y}]={\mathbb{E}}_{\mathbf{x},\mathbf{y}}[\{\mathbf{x}-\mathbb{E}[\mathbf{x}]\}\{{\mathbf{y}}^T-\mathbb{E}[{\mathbf{y}}^T]\}] \\ ={\mathbb{E}}_{x,y}[\mathbf{x}{\mathbf{y}}^T]-\mathbb{E}[\mathbf{x}]\mathbb{E}[{\mathbf{y}}^T](1.42) \end{gathered}$$
并且，当vector $\mathbf{x}$ 本身之间进行cov运算时，我们通常进行简写：$\text{cov}[\mathbf{x}]\equiv \text{cov}[\mathbf{x},\mathbf{x}]$。

1.2.3 Bayesian probabilities

我们在很多时候都需要对各式各样的事物进行分析，分析其发生的概率。如果我们能够本身进行多次实验（例如本章中的取小球例子）的话，我们就可以通过大量实验，对各类情况的结果进行统计，并根据当数据量趋于无穷大时，频率分布将收敛于概率分布的特点，对概率分布进行直接估计。这是频率学派的观点。
然而，又有很多时候，我们根本没法得到很多的数据（正如书中所举的例子：月球之前是否有环绕太阳的可能性？北极冰帽有多大可能性在本世纪末消失？）。这些例子都几乎不能做反复试验，因此频率学派的方法在这里失去了作用。
但是，虽然我们无法预知北极冰帽完全消融的时间，但是我们可以对冰消融的速度进行一个初步的估计。假设此时我们从卫星传回地球的信息中得到了一些新的相关信息，这些信息或多或少会与我们之前的估计有所不同，因此，我们可以根据这些新的信息，对我们之前所做的估计进行修正。由此，我们可以根据我们在修正后的估计，来进行最优的决策。这就是贝叶斯的角度对probability的解释。

我们自然可以使用频率学派的观点，仅将第1.1节中的 $t_n$ 视为variable。但此时，我们需要对参数 $\mathbf{w}$ 的uncertainty进行量化。所以我们需要从贝叶斯的观点去运用probability theory。
此时，回想到在书中，我们在得知取到红球之后，所选择的可能颜色的盒子概率分布也相应地发生了改变。此时，我们再结合Bayes’ theorem本身进行分析，我们可以得到Bayes’ theorem的另外一个作用：它通过吸纳observed data所提供的evidence，将prior probability转换为posterior probability。
联系到参数 $\mathbf{w}$ 上，我们首先对该参数作以初步假设：$p(\mathbf{w})$， 即为该参数的prior probability，然后在得到data $\mathcal{D}=\{t_1,t_2,...,t_N\}$ 之后，我们可以通过 $p(\mathbf{w}|\mathcal{D})$ ，将这些observed data加入进模型，从而得到该参数的posterior probability：
$$p(\mathbf{w}|\mathcal{D})=\frac{p(\mathcal{D}|\mathbf{w})p(\mathbf{w})}{p(\mathcal{D})}(1.43)$$
其中， $p(\mathcal{D}|\mathbf{w})$ 称为“likelihood”，它是参数 $\mathbf{w}$的函数，它使用observed data $\mathcal{D}$ 对当前 $\mathbf{w}$ 下生成数据的可能性进行评估。但要注意的是，likelihood并非是关于 $\mathbf{w}$ 的分布。
而又由于 $p(\mathcal{D})$ 是用于normalization的constant，因此我们可以得到如下关系：
$$\text{posterior}\propto \text{likelihood}\times \text{prior}(1.44)$$
且上式中的三项均为参数 $\mathbf{w}$ 的函数。
而Bayes’ theorem中的denominator可以表示为：
$$p(\mathcal{D})=\int p(\mathcal{D}|\mathbf{w})p(\mathbf{w})\text{d}\mathbf{w}(1.45)$$

那么频率派的参数估计方法，和贝叶斯学派的参数估计方法有什么区别呢？
在频率学派看来，参数 $\mathbf{w}$ 应当是一个定值，频率学派会用某种estimator去估计该参数。那么估计的误差怎么处理，频率学派认为，我们所得到的数据集，其实无法完全表现该数据集的概率分布，由于我们的参数估计是在这个不完整的数据集上进行的，所以我们的误差就来源于observed data所展示给我们的distribution，和真实的distribution之间的偏差。
而在贝叶斯学派看来，我们只有唯一的数据集，即我们的observed data set $\mathcal{D}$（没有别的什么数据了）, 此时对于参数 $\mathbf{w}$ 的估计中出现的uncertainty，则通过对该参数进行probability distribution的分析而得到。
频率学派经常采用maximum likelihood ($p(\mathcal{D}|\mathbf{w})$) 的方法，选出那个能使得该likelihood函数值最大的 $\mathbf{w}$ 的值。而对于error bar的估计则可以使用bootstrap的方法，在原有含N个数据的数据集 $\mathbf{X}$ 中，随机sample出N个数据，组成一个新的数据集，重复L次后，构造出L个这样的数据集。然后分别利用这些数据集进行参数 $\mathbf{w}$ 的估计，并进行prediction。最终通过计算各类prediction结果之间的variability，从而对参数估计中的误差进行计算。
至于使用贝叶斯方法，还是频率派方法，目前仍然处于争议的状态之中。在一个抛硬币的问题中，假设抛3次的结果都是正面，那么用频率派的方法，得到的结果必然是：抛正面的概率为1，负面为0。但我们根据常识可知，一般情况下，抛硬币出现正反面的概率是一样的0.5，所以我们可以将这个常识作为先验知识加入进去，从而使得最终计算出来的概率分布不那么极端（尽管我们抛了3次硬币，且全都是正面朝上）。
但从另外一个角度来讲，prior的加入是纯粹的人为设计，有时候的设计可能只是为了服务于数学推导上的便利，未必就是客观事实的反映。
本书将主要讲述贝叶斯的相关方法，以及频率学派中那些非常有用的方法。
虽然贝叶斯方法的提出时间很早，但它是在近些年来才兴起的。这里面的问题主要在于贝叶斯公式中的分母一般需要在参数上进行integrate out，需要遍历整个参数空间。近年来提出的MCMC方法，以及高速计算机的发展，才为贝叶斯方法带来新的活力。然而，MCMC方法本身对于计算量的消耗很大，因此该方案一般只适用于小规模的问题。更近年来，作为posterior probability的近似方法，变分贝叶斯以及期望传播，这类确定性算法的出现，也成为了MCMC方法的补充。而这些方法都会在后面章节介绍。

1.2.4 The Gaussian distribution

对于连续随机变量，Gaussian distribution是一个非常重要的distribution。假设我们的随机变量是一个single real-valued x的时候，并且设其服从Gaussian distribution，则有x的概率密度函数如下：
$$\mathcal{N}(x|\mu ,{\sigma }^2)=\frac{1}{(2\pi {\sigma }^2{)}^{1/2}}\text{exp}\left\{-\frac{1}{2{\sigma }^2}(x-\mu {)}^2\right\}(1.46)$$
其中，$\mu$被称为mean，${\sigma }^2$被称为variance。${\sigma }^2$ 的算术平方根 $\sigma$ 被称为standard deviation。${\sigma }^2$ 的倒数： $\beta =\frac{1}{{\sigma }^2}$ 被称为precision。
Gaussian distribution如下图所示：

由式(1.46)，我们可以得到如下两条结论（同样也是构成概率密度函数所要满足的基本要求）：
$$\mathcal{N}(x|\mu ,{\sigma }^2)>0(1.47)$$
$${\int }_{-\infty }^{\infty }\mathcal{N}(x|\mu ,{\sigma }^2)\text{d}x=1(1.48)$$
此外，Gaussian distribution的期望可以计算如下：
$$\mathbb{E}[x]={\int }_{-\infty }^{\infty }\mathcal{N}(x|\mu ,{\sigma }^2)x\text{d}x=\mu (1.49)$$
而对于 $x^2$ 的期望有：
$$\mathbb{E}[x^2]={\int }_{-\infty }^{\infty }\mathcal{N}(x|\mu ,{\sigma }^2)x^2\text{d}x={\mu }^2+{\sigma }^2(1.50)$$
因此，我们可以利用x的variance的推导公式，得到：
$$\text{var}[x]=\mathbb{E}[x^2]-\mathbb{E}[x{]}^2={\sigma }^2(1.51)$$
所以说，我们才会将 ${\sigma }^2$ 称为 Gaussian distribution的variance（因为它本来就是Gaussian distribution的variance）。
对于一个distribution来说，它达到最大值时的那一个点被称为“mode”，因此对于Gaussian distribution来说，它的mode在 $x=\mu$ 时达到。

对于D维的随机向量 $\text{x}$ 来说，如果它服从Gaussian distribution，那么其概率密度有：
$$\mathcal{N}(\text{x}|\mu ,\mathbf{\Sigma })=\frac{1}{(2\pi {)}^{D/2}}\frac{1}{|\mathbf{\Sigma }{|}^{1/2}}\text{exp}\left\{-\frac{1}{2}(\text{x}-\mu {)}^T{\mathbf{\Sigma }}^{-1}(\text{x}-\mu )\right\}(1.52)$$
其中D维向量 $\mu$ 是mean，$\mathbf{\Sigma }$ 是covariance。

如果我们有一个dataset，其中包含observations $\mathbf{x}=(x1,...,x_N{)}^T$, 共含有N个1维的observation。我们假设这些observations是我们互相独立地从一个mean和variance未知的Gaussian distribution中取出来的。那么我们该如何得到这个Gaussian distribution的参数？（注：互相独立地从同一个分布中取出来（independent identically distributed， i.i.d））
由于任意两个相互独立的事件的联合概率分布等于二者各自的边缘概率分布的乘积，又因为我们的data 满足 i.i.d 条件，所以我们可以在given $\mu$ 和 ${\sigma }^2$ 的时候，以如下的形式写出得到这个data set的概率：
$$p(\mathbf{x}|\mu ,{\sigma }^2)=\prod _{n=1}^N\mathcal{N}(x_n|\mu ,{\sigma }^2)(1.53)$$
当我们将这个函数看作是以参数 "$\mu$ 和 ${\sigma }^2$" 为自变量的函数时，该函数被称为“likelihood function” 。
一个利用observed data，在某一特定distribution中寻找参数的方法是，最大化likelihood function。而在实际中，为了计算的简便起见，一般普遍上采用likelihood函数的log形式。又由于log函数是单调递增的，所以最大化likelihood的log函数形式，就相当于最大化likelihood本身。式(1.53)经过log转换后的结果如下：
$$\text{ln}p(\mathbf{x}|\mu ,{\sigma }^2)=-\frac{1}{2{\sigma }^2}\sum _{n=1}^N(x_n-\mu {)}^2-\frac{N}{2}\text{ln}{\sigma }^2-\frac{N}{2}\text{ln}(2\pi )(1.54)$$
对 $\mu$ 求导，并令导数为0，可得 $\mu$ 的值为：
$${\mu }_{\text{ML}}=\frac{1}{N}\sum _{n=1}^N{x}_n(1.55)$$
这里的 ${\mu }_{\text{ML}}$ 被称为 sample mean。因为它是所有observations（sample）的mean。
同理，对 ${\sigma }^2$有：
$${\sigma }_{\text{ML}}^2=\frac{1}{N}\sum _{n=1}^N(x_n-{\mu }_{\text{ML}}{)}^2(1.56)$$
其中 ${\sigma }_{\text{ML}}^2$ 被称为 sample variance，因为它是围绕着sample mean ${\mu }_{\text{ML}}$ 来计算的数据点的离散程度。
对这两个量的数学期望进行计算：
$$\mathbb{E}[{\mu }_{\text{ML}}]=\mu (1.57)$$
$$\mathbb{E}[{\sigma }_{\text{ML}}^2]=(\frac{N-1}{N}){\sigma }^2(1.58)$$
可见，sample variance与真实的variance之间相差了一个factor，于是，为了能让估计出来的variance是unbiased的，我们对于 ${\sigma }^2$ 的估计通常写作如下的形式：
$${\sigma }^2=\frac{N}{N-1}{\sigma }_{\text{ML}}^2=\frac{1}{N-1}\sum _{n=1}^N(x_n-{\mu }_{\text{ML}}{)}^2(1.59)$$

1.2.5 Curve fitting re-visited

本节中，我们将重新回顾多项式拟合问题。在之前的章节中，我们知道，多项式拟合问题可以被表示成最小化误差的方式。

回顾一下该问题中的数据：我们有N个输入值$\mathbf{x}=(x_1,x_2,...,x_N{)}^T$, 以及与它们相应的输出（目标）值$\mathbf{t}=(t_1,...,t_N{)}^T$. 我们首先可以考虑对目标变量的uncertainty进行建模，即，对目标变量的概率分布进行建模。因此，我们假设在给定x的时候，输出的t满足一个均值为$y(x,\mathbf{x})$的Gaussian distribution，即

$$p(t|x,\mathbf{w},\beta )=\mathcal{N}(t|y(x,\mathbf{w}),{\beta }^{-1})(1.60)$$
其中$\beta$就是之前提到的精度参数。
我们可以利用下图来形象地展示关于t的uncertainty：

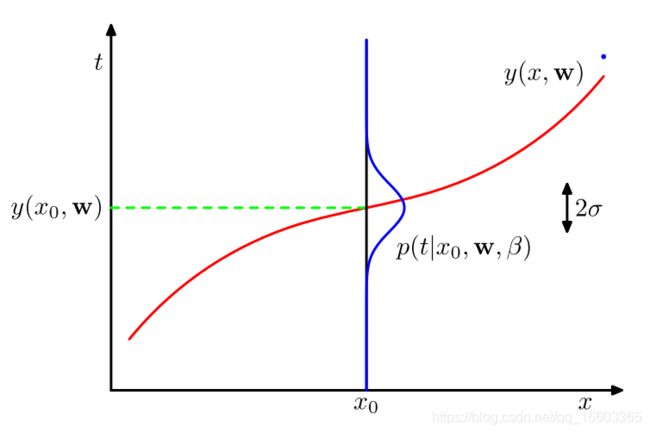
$p(t|x,\mathbf{w},\beta )$是一个关于变量$t$的概率分布函数，但我们同样可以发现，它也是关于变量$\mathbf{w}$的似然函数。因此，我们可以利用该似然函数，来对$\mathbf{w}$的值进行估计:
$$p(\mathbf{t}|\mathbf{x},\mathbf{w},\beta )=\prod _{n=1}^N\mathcal{N}(t_n|y(x_n,\mathbf{w}),{\beta }^{-1})(1.61)$$
正如我们之前所做的，我们可以通过最大化对数似然函数的方式，去对这些的参数$\mathbf{w}$的值进行估计：
$$\text{ln}p(\mathbf{t}|\mathbf{x},\mathbf{w},\beta )=-\frac{\beta }{2}\sum _{n=1}^N\{y(x_n,\mathbf{w}-t_n){\}}^2+\frac{N}{2}\text{ln}\beta -\frac{N}{2}\text{ln}(2\pi )(1.62)$$
我们设${\mathbf{w}}_{\text{ML}}$为maximum likelihood下的多项式参数估计值。我们首先对式(1.62)进行观察，由于该式后两项与$\mathbf{w}$
无关，所以我们可以忽略这两项。又因为该式第一项中的系数仅仅可以对该项进行放缩，所以我们可以将该项$\frac{\beta }{2}$转换为$\frac{1}{2}$, 而我们对该函数的最大化过程等价于对该函数的相反数的最小化过程，因此我们可以将负号去掉，从而最小化该函数。此时我们可以看到，该函数其实是与式(1.2)中的最小化平方和误差，是等价的。因此我们可以说，平方和误差函数与假设目标值服从高斯分布（或者说目标值含有高斯噪声）的最大似然函数之间，在估计参数$\mathbf{w}$的意义下是等价的。
如同前面计算data points服从Gaussian distribution的似然函数一样，我们可以首先算出${\mathbf{w}}_{\text{ML}}$的值（此时${\mathbf{w}}_{\text{ML}}$与$\beta$）在似然函数中解耦。然后将${\mathbf{w}}_{\text{ML}}$值代入原似然函数，我们就可以得到如下的式子：
$$\frac{1}{{\beta }_{\text{ML}}}=\frac{1}{N}\sum _{n=1}^N\{y(x_n,{\mathbf{w}}_{\text{ML}}-t_n){\}}^2(1.63)$$
于是我们便得到$\beta$的值了。

因此，在预测的时候，我们可以将上述两个参数代入原来关于目标值t的概率分布中：
$$p(t|x,{\mathbf{w}}_{\text{ML}},{\beta }_{\text{ML}})=\mathcal{N}(t|y(x,{\mathbf{w}}_{\text{ML}}),{\beta }_{\text{ML}}^{-1})(1.64)$$
此时，我们选择将关于系数$\mathbf{w}$的先验分布加入到该系数的概率分布中，从而以一种更为贝叶斯的方式来表达该系数的分布。我们假设该数服从如下的Gaussian distribution：
$$p(\mathbf{w}|\alpha )=\mathcal{N}(0,{\alpha }^{-1}\text{I})={\left(\frac{\alpha }{2\pi }\right)}^{(M+1)/2}exp\left\{-\frac{\alpha }{2}{\mathbf{w}}^{\text{T}}\mathbf{w}\right\}(1.65)$$
其中$\alpha$是该概率分布的精度参数，$M+1$是$\mathbf{w}$中所含分量的个数。$\alpha$这类用来控制模型参数的变量，被称为“超参数”。
然后，我们利用贝叶斯公式的原理，即后验概率正比于似然函数与先验概率的乘积，遂得到如下的式子：
$$p(\mathbf{w}|\mathbf{x},\mathbf{t},\alpha ,\beta )\propto p(\mathbf{t}|\mathbf{x},\mathbf{w},\beta )p(\mathbf{w}|\alpha )(1.66)$$
于是我们现在可以通过找到那个能使得该后验概率最大的$\mathbf{w}$，作为我们想要的参数$\mathbf{w}$。该方法被称为“最大后验概率”方法，简称MAP。

结合(1.66), (1.62), (1.65)三个式子，我们可以将MAP转换为最小化下式：
$$\frac{\beta }{2}\sum _{n=1}^N\{y(x_n,\mathbf{w})-t_n{\}}^2+\frac{\alpha }{2}{\mathbf{w}}^{\text{T}}\mathbf{w}(1.67)$$
此时我们可以看到，MAP方法与$\lambda =\alpha /\beta$的正则化的最小均方误差函数，是相同的。

1.2.6 Bayesian curve fitting

尽管我们已经将关于参数$\mathbf{w}$的先验分布信息加入进我们关于该参数的概率分布中，但是MAP方法仍然（如同ML方法一样）做的是“点估计”。在一个完整的贝叶斯方法中，我们将利用sum和product rule，对目标值的概率分布进行描述。而在这个过程中，我们需要对$\mathbf{w}$的所有取值进行求和（即对$\mathbf{w}$求积分）。而这个求积分的步骤其实就是在模式识别中，贝叶斯方法的核心。
在进行接下来的步骤之前，我们首先对我们的目标进行回顾：在曲线拟合问题中，我们已经拥有的信息是训练数据：$\mathbf{x},\mathbf{t}$ 除此之外还有一个新的test point x。我们的目标在于，对这个test point x的target value t进行预测。
在这里，我们希望对预测值t的概率分布$p(t|x,\mathbf{x},\mathbf{t})$进行计算。其中我们假设超参$\alpha ,\beta$是已经提前知道了的。
因此，我们可以利用sum和product rule，对t所满足的分布进行计算：
$$p(t|x,\mathbf{x},\mathbf{t})=\int p(t|x,\mathbf{w})p(\mathbf{w}|\mathbf{x},\mathbf{t})\text{d}\mathbf{w}(1.68)$$
其中，$p(t|x,\mathbf{w})$是由(1.60)式得到的，其中的$\alpha ,\beta$都被略去了。$p(\mathbf{w}|\mathbf{x},\mathbf{t})$是关于参数$\mathbf{w}$的后验分布。在3.3节中，我们将会知道，对于curve fitting问题而言，后验分布是一个Gaussian distribution，并且该Gaussian distribution是可以计算得到其解析解的。相似的，这个关于t的概率分布也是一个Gaussian distribution的形式，我们不加证明（在3.3节会具体说明）地给出这个Gaussian distribution的具体形式：
$$p(t|x,\mathbf{x},\mathbf{t})=\mathcal{N}(t|m(x),s^2(x))(1.69)$$
其中均值和方差为：
$$m(x)=\beta \varphi (x{)}^{\text{T}}\mathbf{S}\sum _{n=1}^N\varphi (x_n)t_n(1.70)$$
$$s^2(x)={\beta }^{-1}+\varphi (x{)}^{\text{T}}\mathbf{S}\varphi (x)(1.71)$$
其中矩阵$\mathbf{S}$的计算如下：
$${\mathbf{S}}^{-1}=\alpha \mathbf{I}+\beta \sum _{n=1}^N\varphi (x_n)\varphi (x{)}^{\text{T}}(1.72)$$
其中$\mathbf{I}$为单位矩阵，且向量$\varphi (x)$中的每一个元素${\varphi }_i(x)=x^i,\text{for}i=0,...,M$
(1.71)式的第一项所建模的是预测值$t$的uncertainty（由t值上的noise所带来的），而第二项所要建模的是参数$\mathbf{w}$中的uncertainty，这个uncertainty其实就是Bayesian方法的一个结果。

1.3 Model Selection

在使用最小二乘法的curve fitting问题中，我们知道一定存在一个最优的多项式次数M，使得这个模型具有最好的泛化能力。多项式的次数控制着模型中自由参数的数量，从而对模型的复杂度进行了控制。在正则化的最小二乘中，正则系数$\lambda$同样也控制着模型的复杂度。
在实际中，我们通常需要对这些参数的值进行确定，从而使得模型在new data上能够有最好的表现。此外，我们同样也希望能够在参数确定时比较不同的模型，从而挑出一个最好的模型用于我们具体的数据集。
我们通过对于最大似然方法的研究发现，由于潜在的over-fitting的缘故，模型在training set上的表现可能会特别好，但是我们知道，这种“好”的效果并不能代表模型真正的泛化能力（模型的泛化能力才是我们所关注的），因而不能作为模型在unseen data上的表现。当我们的数据量充足时，我们可以选择training set中的一部分数据用于训练，另一部分数据用于比较不同参数选择（或不同模型下）这些模型之前的性能差异，我们将这样的数据称为validation set。然后挑出其中validation set上表现最好的模型。
若因为一些特殊的原因，模型需要在有限的数据集上进行多次迭代训练，那么该模型很有可能在validation set上表现出overfitting的问题。因此设置一个独立出来的test set用于评估模型的最终性能，是十分有必要的。
在数据量有限的情况下，由于我们需要尽可能多的数据用于训练，因此validation set的大小就会变得非常小。而规模小的validation set具有相对较大的noisy estimate，因此我们采用cross-valiation的做法，如下图所示：

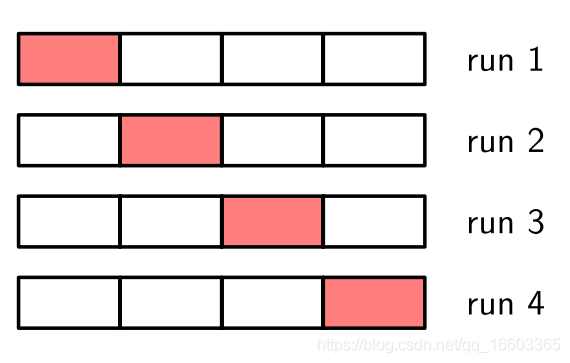
这里我们将数据分为4份（S=4）。
对于每一个模型，我们分别训练四次，每一次分别用不同的一部分数据作为validation set，同时使用另外的所有数据作为training set。从而尽可能规避noisy estimate的问题。
当S=N时（N为data point的总数），我们称这样的方法为leave-one-out 技术。
cross-validation方法的缺点在于，我们对一个模型的训练次数随着S的增大而增大。而当我们有许多不同的模型参数的选择，以及许多不同的模型架构时，所有模型的总训练次数还会不断增高。而当模型训练一次本身的代价就十分大的时候，这样的问题将会更为严重。
关于以上问题，我们是否有一个解决方案呢？在历史上，有许多的“information criteria”相继提出，这些方法的目的在于修正因最大似然估计所带来的bias。其解决思路是为那些由于模型复杂而导致的overfitting增加惩罚项。例如，AIC(Akaike information criterion) 方法选择那一个能使得下式值最大的模型：
$$\text{ln}p(\mathcal{D}|{\mathbf{w}}_{\text{ML}})-M(1.73)$$
其中$p(\mathcal{D}|{\mathbf{w}}_{\text{ML}})$是在log likelihood的最优值，M为模型中可调整参数的个数。关于该方法的一个变体BIC，将在4.4.1节进行详细介绍。

1.4 The Curse of Dimensionality

本节所要讲述的是“Curse of Dimensionality”。关于这一章，所要阐明的问题其实有两方面：1. 维数增长带来的困境；2. 低维与高维数据分布之间特性的差异。
在之前所讲的例子里，我们对于输入数据的要求都是一维的。然而在实际情况中高维输入数据才是普遍情况。为了更好的阐述这个问题，我们利用附录A里面的一个“石油”、“水”、“气体”混合物的例子。附录这部分可以不看，因为那里的信息过于繁琐。我们简要叙述如下。对于这三种物质的混合情况，主要分为三类“分层的”“环形的”“均匀的”。我们已知关于混合物的12种测量属性（也就是input的12个分量），我们的目的在于，利用这12个属性，来对（具这12个属性的）混合物的混合类型进行分类。

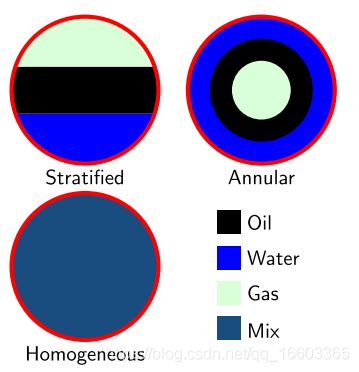
上图所示为三种类型的混合物。
为了方便起见，我们只采用input中的第6个和第7个分量。如下图所示：

该图所示，为training set中的各个data point，不同的颜色代表不同类型的混合物。假如我们得到了一个新的unseen data（在图中以黑色的“叉号”体现），那么我们如何知道这个点是属于哪一种类型的混合物呢？此时一种直观的想法是，它离哪一个点近，那么就更有可能是哪一种类型的混合物。我们可以看到，这个点离红色或绿色都很近，说明它很有可能与红色点/绿色点属于同一类别。同样我们可以发现，这个点离蓝色点较远，于是我们可以看到，这个点不太可能与蓝色点是同类的。
那么，我们如何将这里的描述转换为某一种具体的算法呢？一种想法是，利用分格投票的方式。如下图所示：

我们将输入空间划分成一个个的格子， 对于每一个格子，若这个格子中某一种颜色点的占比最大，那么新来到这个格子里的点，就属于这个颜色下的类别。
然而，当维数增大时，这样的方法会出现许多问题。首先，当维数增大时，我们需要划分的格子数也会以指数的方式增大。那么为了与之匹配，我们的数据量也需要占据这些格子，因此也需要以指数的趋势进行增长。我们知道，这对于我们而言几乎是不现实的。
我们将注意力转回curve fitting问题上，对于该问题，如果我们的输入是D维的，那么我们可以得到如下的多项式方程（以三阶方程为例）：
$$y(\mathbf{x},\mathbf{w})=w_0+\sum _{i=1}^D{w}_i{x}_i+\sum _{i=1}^D\sum _{j=1}^D{w}_{ij}{x}_i{y}_j+\sum _{i=1}^D\sum _{j=1}^D\sum _{k=1}^D{w}_{ijk}{x}_i{x}_j{x}_k(1.74)$$
因此，这里的系数以$D^M$的趋势，随着维数D的增大而增大。虽然这里的增长趋势实质上是幂次的，然而当维数很大时，模型也会由于参数过多而变得不可控，从而导致该方法的应用范围受限。

然后我们来讨论低维特性到高维特性的巨大不同。我们生活在三维空间里，因此我们的很多直觉其实都是以我们所生活的三维空间为基础，来进行构建的。然而，高维空间里的很多特性其实是反直觉的。我们以在极坐标系下的多维高斯分布为例。
假设我们有两个球体，一个半径r=1, 另一个半径r=$1-ϵ$， 我们有D维球体的方程：
$$V_D(r)=K_D{r}^D(1.75)$$
其中我们可以计算得到厚度为$ϵ$的薄层在r=1的球体中所占的比例为：
$$\frac{V_D(1)-V_D(1-ϵ)}{V_D(1)}=1-(1-ϵ{)}^D(1.76)$$
对于高斯分布的概率密度函数$p(r)$，其中r为原点到当前点的距离。那么$p(r)\delta r$其实就是在一个厚度为$\delta r$内，在半径为r时的薄壳。而通过下图所示：

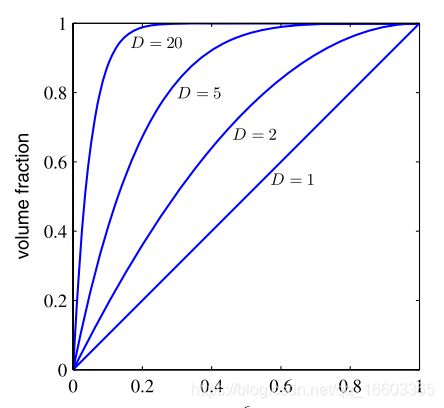
当维数增大时，高斯分布的概率更多集中于球体表面的薄壳中。

这个例子对于我们的启示在于，我们不能将维度在低维上的经验直接推广到高维上。

虽然高维空间有着curse of dimensionality的问题，然而我们同样有一些方法去解决它们。一种角度是针对那些虽然在高维空间，但实际上有效空间是一个低维的空间的数据。我们可以在低维空间中去处理相应的问题；另一个方法是，得到的数据可能是比较平滑的，因此我们可以通过局部插值的方式，得到一条较为平滑的函数曲线，从而对unseen data的相应target value进行预测。

1.5 Decision Theory

在1.2节中，我们已经对uncertainty进行了建模。本节讨论的decision theory其实就是在1.2节的基础上，在模式识别中出现uncertainty的情况下，所采取的最优决策问题。
假设我们的输入为vector $\mathbf{x}$, 输出为vector $\mathbf{t}$, 在回归问题中，$\mathbf{t}$是一个具有连续型分量的向量；在分类问题中，$\mathbf{t}$是一个个class label。由于联合概率分布$p(\mathbf{x},\mathbf{t})$包含了关于这些变量的所有uncertainty的信息，因此通过training data来对这一概率分布进行求得，就是一个在inference中十分重要且困难的问题，关于这一问题的求解，也是本书中的主体部分中所要讨论的问题。然而，在实际应用中，我们往往需要对t的值进行预测，而这种预测的行为就构成了本节所讲的decision theory的基础理论。
考虑一个医学诊断的问题，我们通过X-ray来诊断病人，从而去推断这个病人是否罹患癌症。在这个问题中，我我们的输入是X-ray的像素点信息，即vector $\mathbf{x}$, 输出的t表示这张图片中是否出现了癌症，若出现了，则属于类别${\mathcal{C}}_1$（t=0）, 否则则属于类别${\mathcal{C}}_2$（t=1）。通常的推断问题一般的目的在于确定联合概率分布$p(\mathbf{x},{\mathcal{C}}_k)$, 或者是$p(\mathbf{x},t)$, 这个联合概率分布给予了我们这种情况下完整的概率描述。但是我们同样需要注意的是，我们最终的关注点在于，判断病人是否患癌。由于我们需要这样的一个决策是给定要求下最优的，因此我们还需要一个decision step，而该decision step是decision theory中的主要内容。当然，我们将会看到，当我们完成了inference problem之后，这个decision stage将会变得十分简单，甚至是不重要。
接下来的部分中，我们首先对概率在这个决策过程中所起到的作用进行阐述。
当我们已经得到X-ray后的image $\mathbf{x}$之后，我们的兴趣点就着眼在这个image是属于两个类别分别的概率 :
$$p({\mathcal{C}}_k|\mathbf{x})=\frac{p(\mathbf{x}|{\mathcal{C}}_k)p({\mathcal{C}}_k)}{p(\mathbf{x})}(1.77)$$
我们注意到，上述贝叶斯定理中的所有组件都可以从联合概率分布$p(\mathbf{x},{\mathcal{C}}_k)$中得到。我们将$p({\mathcal{C}}_k)$视为类别${\mathcal{C}}_k$的概率分布，而将$p({\mathcal{C}}_k|\mathbf{x})$视为相应的后验分布。因此，$p({\mathcal{C}}_1)$表示我们在得到X-ray image之前，患者患癌的概率，而将$p({\mathcal{C}}_1|\mathbf{x})$表示我们在得到image $\mathbf{x}$ 之后，患者患癌的概率分布。如果我们希望分类中错误分类的概率最小，从直觉上来说，我们应该将given image $\mathbf{x}$时后验概率分布最高的那一个类别作为我们最终选择的类别。

1.5.1 Minimizing the misclassification rate

最小化分类率问题中的目标在于，我们需要尽可能的减少错误分类率。首先我们需要将每一个点划分到一个个的区域中，在特定的区域中，这些点会被划分到特定的类别里。这些区域${\mathcal{R}}_k$被称为decision region， 而在这个区域内的所有点将被归类到类别${\mathcal{C}}_k$中。这些区域之间的边界被称为decision boundaries。其中这些区域不一定要连接在一起，我们允许同一种类别拥有多个不连续的区域块。错误分类发生在一个本属于区域${\mathcal{C}}_1$的data point被分类到区域${\mathcal{C}}_2$中。这种情况发生的概率为：
$$p(\text{mistake})=p(\mathbf{x}\in {\mathcal{R}}_1,{\mathcal{C}}_2)+p(x\in {\mathcal{R}}_2,{\mathcal{C}}_1)={\int }_{{\mathcal{R}}_1}p(\mathbf{x},{\mathcal{C}}_2)\text{d}\mathbf{x}+{\int }_{{\mathcal{R}}_2}p(\mathbf{x},{\mathcal{C}}_1)\text{d}\mathbf{x}(1.78)$$
这个公式就是错误分概率的公式。其中，当$p(\mathbf{x},{\mathcal{C}}_1)>p(\mathbf{x},{\mathcal{C}}_2)$时，即（$p(\mathbf{x},{\mathcal{C}}_k)=p({\mathcal{C}}_k|\mathbf{x})p(\mathbf{x})$）时，我们可以选择后验概$p({\mathcal{C}}_k|\mathbf{x})$更大的那个类别，作为该点的类别。此时能够将错误分类率降到最低。
对于这个公式的理解，其实是这样的。如果对于一个data point x，它分类到类别1的概率p(C1|x)
=0.6, 而分类到类别2 的概率是p(C2|x)=0.4, 那么如果我们将它最终分类到类别1，它就有40%的可能性是分类错误的，因此我们可以说“这个点”分类错误的概率是0.4。那么如果我们有一个数据集，其中包含很多的点，此时分类错误的概率该如何去计算呢。显然的方法是，统计每一个点的实际分类情况，然后得到这个点的错误分类率，然后将所有点的错误分类率加和，并求平均，于是便得到了整个数据集在该模型下的错误分类率。而我在这里所述的这个错误分类器，其实与公式(1.79)的含义相同。我们在求平均的时候，实际上就计算得到了每一个点的$p(\mathbf{x})$, 当我们得到这个值之后，我们实际上就已经通过$p({\mathcal{C}}_k|\mathbf{x})\cdot p(\mathbf{x})$的方式，得到(1.78)式。
对于更多的类别（例如K个类别），我们可以使用正确分类率，并通过最大化该分类率的方式，对最终的分类率进行计算：
$$p(\text{correct})=\sum _{k=1}^{K}p(\mathbf{x}\in {\mathcal{R}}_k,{\mathcal{C}}_k)=\sum _{k=1}^K{\int }_{{\mathcal{R}}_k}p(\mathbf{x},{\mathcal{C}}_k)\text{d}\mathbf{x}(1.79)$$
与最小化(1.78)式同理，如果我们要对(1.79)式进行最大化，那么我们只需要将每一个点对应的那个能使得式$p({\mathcal{C}}_k|\mathbf{x})$概率最大的那个点即可.

1.5.2 Minimizing the expected loss

对于很多问题，我们可能更倾向于避免某一种分类错误的情况。例如，在诊断癌症中，如果一个健康的人被误认为罹患癌症，那么他至多感到沮丧，并接受进一步的诊断。但如果一个患有癌症的人被诊断为健康，这个问题会变得严重许多。我们显然希望在第二种情况中犯更少的错误。为此，我们构建一个loss function，用以处理这些类似的情况。假设对于一个input $\mathbf{x}$, 其真实的类别是${\mathcal{C}}_k$, 我们将其分类给类别$j$, 其中j未必与k相同。此时，我们引入一种对loss的加权机制，即矩阵$L$, 其中每一个元素$L_{kj}$表示实际类别为k的data point，被分类到j时的loss。
在这个问题中，该loss matrix如下图所示：

这里的loss matrix说明了，如果对于正确的分类，这里不存在任何的loss；然而，对于错误的分类，不同情况的loss是不同的，如果一个人没有癌症，但被误诊为癌症，那么这个人相应的loss为1；反之，如果一个人实际患有癌症，但被误诊为没有癌症，那么这个情况下相应的loss为1000.
然而实际情况中，我们并不知道每一个data point相应的true class究竟是什么。对于一个input $\mathbf{x}$, 我们关于true class的所有uncertainty都通过联合概率分布$p(\mathbf{x},{\mathcal{C}}_k)$来表示。因此，虽然我们没法得到关于分类错误的loss，但是我们可以计算分类错误的平均loss：
$$\mathbb{E}[L]=\sum _k\sum _j{\int }_{{\mathcal{R}}_j}{L}_{kj}p(\mathbf{x},{\mathcal{C}}_k)\text{d}\mathbf{x}(1.80)$$
在上式中，每一个$\mathbf{x}$都被分配给了某一个region ${\mathcal{R}}_j$, 我们的目标是，对各个${\mathcal{R}}_j$进行合理的划分，进而使得这个loss的值最小。
并且，通过上式我们可以发现，其实对于每一个$\mathbf{x}$, 我们的目的实际上在于，为它选择最为合适的region ${\mathcal{R}}_j$，使得${\sum }_k{L}_{kj}p(\mathbf{x},{\mathcal{C}}_k)$最小。由因为$p(\mathbf{x},{\mathcal{C}}_k)=p({\mathcal{C}}_k|\mathbf{x})$, 并且对于同一个$\mathbf{x}$而言，这个$p(\mathbf{x})$的值是一样的。因此，我们可以略去这里的$p(\mathbf{x})$, 对于每一个$\mathbf{x}$, 我们需要最小化的loss是：
$$\sum _k{L}_{kj}p({\mathcal{C}}_k|\mathbf{x})(1.81)$$

1.5.3 The reject option

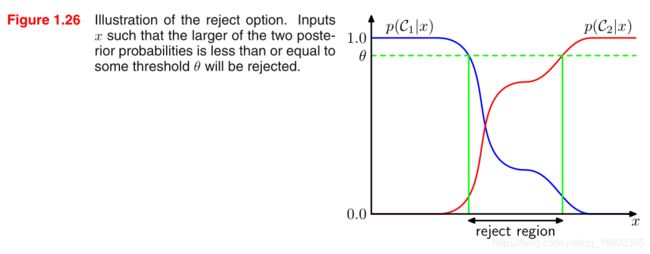
我们在进行决策时，往往选择那一个能使得$p({\mathcal{C}}_k|\mathbf{x})$值最大的那个类别k。然而，当这个类别下的条件概率本身远小于1，或者说有好几个类别具有同一个数量级上的概率值（也就是说，这些概率值相近）时，如果我们直接根据这个条件概率的大小来进行自动决策的话，就会导致loss升高。在一些应用中，避免在这些难以分类的例子中进行分类，是十分有必要的。这就是所谓的reject option。例如，对于前述的X-ray image classification问题，如果我们遇到一些不易分类的例子，那么我们可以拒绝分类它们，并将它们的分类任务转给人类专家去做。为了实现这儿reject option，我们可以建立一个threshold $\theta$, 如果最大的后验概率 $p({\mathcal{C}}_k|\mathbf{x})$的值都小于等于这个$\theta$的话，我们就让机器拒绝分类这个image。
下图所示为一个输入变量为1维，输出为2分类的例子：

1.5.4 Inference and decision

对于一个分类问题，我们将其分割成两个stages：inference stage 以及 decision stage。在inference stage中，我们的目的在于使用training data去学习模型中的后验分布$p({\mathcal{C}}_k|\mathbf{x})$; 在decision stage中，我们利用这些后验概率分布来进行最优的类别分配。另外一种解决分类问题的方法通过学习出一个函数（称为“判别函数”）的方式，将输入$\mathbf{x}$映射到具体的decisions中。
事实上，我们有三种方式来解决决策问题，我们按照模型的复杂度由高到低罗列如下：

（a） 首先，为每一个class k建立条件概率密度$p(\mathbf{x}|{\mathcal{C}}_k)$。同时，得到class k的先验概率$p({\mathcal{C}}_k)$。然后我们通过贝叶斯公式计算后验概率分布：
$$p({\mathcal{C}}_k|\mathbf{x})=\frac{p(\mathbf{x}|{\mathcal{C}}_k)p({\mathcal{C}}_k)}{p(\mathbf{x})}(1.82)$$
分母的计算可以利用分子进行：
$$p(\mathbf{x})=\sum _{k}p(\mathbf{x}|{\mathcal{C}}_k)p({\mathcal{C}}_k)(1.83)$$
在这个过程中，我们实际上就已经将联合概率分布$p(\mathbf{x},{\mathcal{C}}_k)$建立好了。
我们称能够建立input与output的联合分布的方法为“generative model”。因为通过这种方法生成出input space中的数据。

**（b）**首先计算得到后验分布$p({\mathcal{C}}_k|\mathbf{x})$, 然后利用decision theory，将每一个新的$\mathbf{x}$赋予到其中一个class。直接建模后验分布的方法被称为“discriminative model”。

**（c）**找到一个被称为“discriminant function”的函数$f(\mathbf{x})$，该函数将输入$\mathbf{x}$直接映射为某一个输出的label。

然后我们来对这三种方法进行对比分析。第一种方法中，由于我们需要计算联合概率分布$p({\mathcal{C}}_k,\mathbf{x})$。而在实际情况中，由于$\mathbf{x}$可能存在维数较高的问题，因此我们可能需要许多的数据作为training set，才能使得这个class-conditional density可以得到一个较为精确的结果（回忆到curse of dimension中，当input space增大时，我们对于数据量的需求也出现了指数增长的趋势）。而prior $p({\mathcal{C}}_k)$的计算就要简单许多，因为我们只需要统计training set中各个class出现的比例即可。然而，方法（a）的一个优势在于，我们可以通过式(1.83), 将数据$\mathbf{x}$的边缘概率分布$p(\mathbf{x})$直接计算出来。这样的概率分布往往可以被用于检测那些在该概率分布下概率值十分小的new data，这样的new data被称为outlier，而这样的方法被称为outlier detection/ noverlty detection.

但是，如果我们仅仅希望去做一个分类任务，方法（a）由于计算量大且需要很多数据的问题其实完全是不必要的。此时我们可以直接通过方法（b），计算得到后验概率分布$p(\mathbf{x},{\mathcal{C}}_k)$。

对于方法（c），我们通过一个判别函数，将输入$\mathbf{x}$直接映射成一个label。但是，方法（c）存在着一个问题，即它不嫩计算出后验概率分布$p({\mathcal{C}}_k|\mathbf{x})$。而后验概率分布十分重要，理由如下：

Minimizing risk: 如果我们的loss matrix发生改变，那么如果我们使用的是后验概率分布，那么我们最终的loss function只需要作以少量的修改；然而，如果我们选用的（c）中的判别函数，那么我们需要完全重新训练一个模型。

Reject option：这个内容在前面讲过。当我们有后验分布时，我们可以通过建立threshold $\theta$的方式，获取到那些比较ambiguous的data point，然后把这些data point交给 human expert去进行分类。

Compensating for class prior：当出现数据不平衡时，即当某一个类别的数据量很少的时候，我们可以首先人为挑选数据，使得类别间数据量均衡，然后再model posterior。
由于posterior正比于prior，而这里的prior又与我们training时所用的数据集有关（此时training用的数据集是人为构造的）。因此，为了消除人为影响，针对posterior，我们可以首先除以该类别在人为数据集中所占的比例，然后再乘以该类比在我们实际数据集中的比例。最终对得到的新的这些posterior进行normalized。

Combining models：对于我们有多种数据的情况（比如既有x-ray image,又有blood data）时，我们未必要将这两种数据合成一个大的input data，而是分别对二者构建后验概率分布。由于二者数据之间是在given分类的基础上是conditional independent的，所以我们可以用这2个posterior之间的乘积进行联合概率分布的计算。
设X-ray image的input是${\mathbf{x}}_{\text{I}}$, 而${\mathbf{x}}_{\text{B}}$是blood data的input，那么这个条件独立关系可以写为：
$$p({\mathbf{x}}_{\text{I}},{\mathbf{x}}_{\text{B}}|{\mathcal{C}}_k)=p({\mathbf{x}}_{\text{I}}|{\mathcal{C}}_k)p({\mathbf{x}}_{\text{B}}|{\mathcal{C}}_k)(1.84)$$
因此，在给定X-ray image以及blood data的时候，后验概率分布为：
$$\begin{gathered} p({\mathcal{C}}_k|{\mathbf{x}}_{\text{I}},{\mathbf{x}}_{\text{B}})\propto p({\mathbf{x}}_{\text{I}},{\mathbf{x}}_{\text{B}}|{\mathcal{C}}_k)p({\mathcal{C}}_k) \\ \propto p({\mathbf{x}}_{\text{I}}|{\mathcal{C}}_k)p({\mathbf{x}}_{\text{B}}|{\mathcal{C}}_k)p({\mathcal{C}}_k) \\ \propto \frac{p({\mathcal{C}}_k|{\mathbf{x}}_{\text{I}})p({\mathcal{C}}_k{\mathbf{x}}_{\text{B}})}{p({\mathcal{C}}_k)}(1.85) \end{gathered}$$
其中，式(1.84)其实就是一个naive Bayes model的例子。

1.5.5 Loss functions for regression

之前我们所讨论的都是关于classification problem的decision theory，现在我们来探讨regression problem的情况（以之前的curve fitting问题为例）。对于regression problem而言，decision stage的目的在于，对于每一个input $\mathbf{x}$,选择一个特定$y(\mathbf{x})$作为对于真值$t$的估计。假设在这种操作之下，我们可以得到loss $L(t,y(\mathbf{x}))$, 类比于之前在分类问题中对loss matrix的利用，我们可以得到最终的loss 表达式：
$$\mathbb{E}[L]=\int \int L(t,y(\mathbf{x}))p(\mathbf{x},t)\text{d}\mathbf{x}\text{d}t(1.86)$$
在regression problem中，对于loss function的一个常用选择是squared loss, 即：$L(t,y(\mathbf{x}))=\{y(\mathbf{x}-t){\}}^2$。因此，loss的期望可以被写为：
$$\mathbb{E}[L]=\int \int \{y(\mathbf{x})-t{\}}^{2}p(\mathbf{x},t)\text{d}\mathbf{x}\text{d}t(1.87)$$
我们的目标在于，寻找到一个$y(\mathbf{x})$, 使得$\mathbb{E}[L]$的值最小。一种常用的方式是采用变分法（变分法的具体内容见附录D）：
$$\frac{\delta \mathbb{E}[L]}{\delta y(\mathbf{x})}=2\int \{y(\mathbf{x}-t)\}p(\mathbf{x},t)\text{d}t=0(1.88)$$
然后我们利用sum rule和product rule，将$y(\mathbf{x})$求解出来：
$$y(\mathbf{x})=\frac{\int tp(\mathbf{x},t)\text{d}t}{p(\mathbf{x})}=\int tp(t|\mathbf{x})\text{d}t={\mathbb{E}}_t[t|\mathbf{x}](1.89)$$
这个结果其实就是，在given $\mathbf{x}$的时候，t的均值，也就是所谓的regression function，如下图所示：

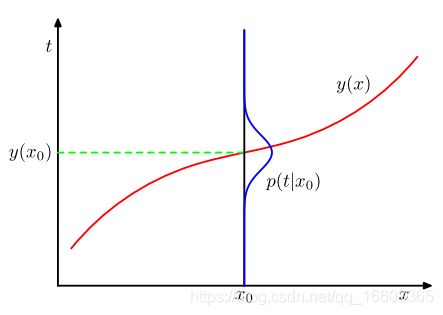
这个结论可以很容易地被推广到多元目标变量中去：即对于target variables $\mathbf{t}$, 它的最优解是条件平均：$y(\mathbf{x})={\mathbb{E}}_t[\mathbf{t}|\mathbf{x}]$。
对于这个结论，我们还可以不通过变分法来得到，即：
$$\begin{gathered} \{y(\mathbf{x})-t{\}}^2=\{y(\mathbf{x})-\mathbb{E}[t|\mathbf{x}]-t{\}}^2 \\ =\{y(\mathbf{x})-\mathbb{E}[t|\mathbf{x}]{\}}^2+2\{y(\mathbf{x})-\mathbb{E}[t|\mathbf{x}])\}\{\mathbb{E}[t|\mathbf{x}]-t\}+\{\mathbb{E}[t|\mathbf{x}]-t{\}}^2 \end{gathered}$$
我们首先对t进行积分，消去交叉项，然后得到loss function：
$$\mathbb{E}[L]=\int \{y(\mathbf{x})-\mathbb{E}[t|\mathbf{x}]{\}}^{2}p(\mathbf{x})\text{d}\mathbf{x}+\int \text{var}[t|\mathbf{x}]p(\mathbf{x})\text{d}\mathbf{x}(1.90)$$
由于我们的目的是寻找一个$y(\mathbf{x})$, 能够使得上式值最小，因此我们只需要使第一项最小即可，此时$y(\mathbf{x})=\mathbb{E}[t|\mathbf{x}]$。这与我们之前得到的结论相符。
式中的第二项是变量t的方差在x上的均值，它表示的是target data的固有variability，并且可以被视为noise。而由于这个noise与$y(\mathbf{x})$之间是相互独立的，因此它表示着loss function的irreducible minimum value。

类似于之前给出的三种解决classification问题的方法，这里给出了三种解决regression问题的方法。

（a）：首先通过计算联合概率分布$p(\mathbf{x},t)$的方式解决inference problem，然后通过归一化的方式得到条件概率密度$p(t|\mathbf{x})$,最终通过marginalize的方式得到条件均值(1.89)。

（b）：首先得到条件概率密度：$p(t|\mathbf{x})$, 然后通过marginalize的方法(1.89)得到条件均值。

（c）：从training data中直接得到一个regression function $y(\mathbf{x})$。

这三种方法的特点与比较，在分类部分已经具体说明过了，因此不赘述。

在很多情况下，squared loss并不是唯一的一种关于regression中loss function的选择。实际上，在许多实用，squared loss最终会导致十分不好的结果。

我们在此简要介绍一种被称为Minkowski loss的loss函数，它的期望计算如下：
$$\mathbb{E}[L_q]=\int \int |y(\mathbf{x})-t{|}^{q}p(\mathbf{x},t)\text{d}\mathbf{x}\text{d}t(1.91)$$
当$q=2$时，这个式子将归约到squared loss。并且当$q=2$时，这个式子取得最小值时的y为conditional mean；对于$q=1$, 为conditional median；对于$q\to 0$, 为conditional mode。

1.6 Information Theory

在前面的部分中，我们介绍了本书中的基础理论，即“概率论”和“决策论”。在本节中，我们将对一些补充理论，即“信息论”进行介绍。

我们首先对离散型随机变量$x$进行讨论，并且我们探究的问题在于，当我们观察到一个关于这个变量的特定值的时候，我们能够接收到的信息有多少？我们把信息量看作是在学习这个变量x上的“惊讶程度”。如果我们得知，一个非常有可能不会发生的事件发生了，那么相比于那些很可能发生的事件而言，前者蕴含着更多的信息量。并且，对于必然要发生的事件，我们其实什么信息都接收不到。根据上述分析，我们发现，一个事件的信息含量是与该事件发生的“概率”密切相关。因此，我们自然可以想到，在进行概率的度量时，相应事件x的概率值$p(x)$是十分重要的。因此，我们需要寻找一个函数$h(x)$，使得该函数是关于$p(x)$的单调函数，并且有该函数可以对信息含量进行定量描述。

我们注意到，如果有两个事件x和y，这两个事件是unrelated，那么至于观察这两个事件的信息增益，其完全等价于这两个事件分别的信息增益之和，因此我们有$h(x,y)=h(x)+h(y)$。并且由于这两个事件之间是相互独立的，于是有$p(x,y)=p(x)p(y)$。根据上述两个关系，我们可以得知，$h(x)$实际上是$p(x)$的logarithm。

因此我们有：
$$h(x)=-{\text{log}}_{2}p(x)(1.92)$$
其中负号表示，信息是一个非负数。并且我们注意到，第概率的事件对应了高信息含量。此外，这个式子中的log函数底数的选取其实没有严格的要求，在信息论中，我们一般取底数为2，此时$h(x)$的单位被称为bits。

此时，假设一个sender想要把一个random variable的value传送给一个receiver，那么在平均意义上，每一次传输的信息量为：
$$H[x]=-\sum _{x}p(x){\text{log}}_{2}p(x)(1.93)$$
这一个重要的关于随机变量x的量被称为quantity。我们注意到，${\text{lim}}_{p\to 0}\text{ln}p=0$,因此，当我们遇到$p(x)=0$的情况时，我们有$p(x)\text{ln}p(x)=0$。

之后书上有一个关于对各种状态编码的例子，这个例子很简单，就不再细讲。最终说明的结论是，entropy和shortest coding length这两者是一样的东西。并且，noiseless coding theorem表明，entropy是传输state of random variable的编码长度的lower bound。

然后，我们通过自然底数来定义entropy，并且这种定义方式也与本书中其他地方的定义相符合。

我们之前是通过表达随机变量状态的信息量的平均，作为对entropy的介绍的。但是事实上，entropy有一个在物理学上，更早的起源。最初它在热能动力理论中被提出，然后它被用于描述统计力学中的无序性。

关于这个角度的理解，我们可以假设我们有N个同样的物体，我们有一系列的箱子，其中第i个箱子中有$n_i$个物体。考虑到把物体分配给箱子的所有可能情况，并且不考虑每一个箱子中物体的顺序，因此，对于N个物体，所有的分配情况有：
$$W=\frac{N!}{{\prod }_i{n}_i!}(1.94)$$
我们将其称为“多重性”。此时，entropy被定义为这个多重性的log形式，并通过适当的常数进行scaled：
$$H=\frac{1}{N}\text{ln}W=\frac{1}{N}\text{ln}N!-\frac{1}{N}\sum _i\text{ln}{n}_1!(1.95)$$
我们考虑当$N\to \infty$的情况，此时分数$n_i/N$就被固定住了，然后我们采用Stirling’s approximation：
$$\text{ln}N!\simeq N\text{ln}N-N(1.96)$$
于是我们有：
$$H=-{\text{lim}}_{N\to \infty }\sum _i\left(\frac{n_i}{N}\right)\text{ln}\left(\frac{n_i}{N}\right)=-\sum _i{p}_i\text{ln}{p}_i(1.97)$$
其中，我们利用了等式${\sum }_i{n}_i=N$并且，有$p_i={\text{lim}}_{N\to \infty }(n_i/N)$, 它代表一个物体被分到第$i$个盒子里的概率。

我们可以将盒子解释为随机变量X的状态$x_i$，其中有$p(X=x_i)=p_i$。此时，有随机变量X的entropy为：
$$H[p]=-\sum _{i}p(x_i)\text{ln}p(x_i)(1.98)$$
对于那些在某些点比较高，而大部分点比较低的概率分布$p(x_i)$，其entropy本身也较低。而对于那些概率分布随取值比较平均的$p(x)$，其entropy值也较高。由于$0\le p_i\le 1$的缘故，entropy的值是非负的。当$p_i=1$且任何其他的$p_{j\ne i}=0$时，该概率分布的entropy为0。
我们可以通过最大化归一化条件的拉格朗日函数的方式：
$$H=-\sum _{i}p(x_i)\text{ln}p(x_i)+\lambda \left(\sum _{i}p(x_i)-1\right)(1.99)$$
得到那个能使得entropy最大的离散随机变量分布。
于是我们可以得到一个这的分布列$p(x_i)$, 其中它的每一个分量下概率取值是相同的，都是$p(x_i)=1/M$, 其中$M$是状态$x_i$的总数。这个结论我们也可以通过Jensen’s inequality的方式得到。为了确认我们得到的驻点就是我们要求的最大值，我们对原函数进行二阶偏导运算，并得到：
$$\frac{\partial H}{\partial p(x_i)\partial p(x_j)}=-I_{ij}\frac{1}{p_i}(1.100)$$
其中$I_{ij}$是单位矩阵中的元素。

现在我们来考虑连续型随机变量的entropy。刚才我们已经定义好了离散型随机变量的entropy，我们可以以这个为基础，定义连续型随机变量的entropy。设该随机变量$x$的概率密度函数为$p(x)$。我们仿照刚才利用箱子装取值的方法，将x的取值划分为一个个间距大小为$\nabla$的区域（每一个区域作为一个箱子），此时由于我们假设$p(x)$是连续的，因此我们可以由中值定理知道，对于每一个箱子，其中存在一个$x_i$, 使得：
$${\int }_{i\Delta }^{(i+1)\Delta }p(x)\text{d}x=p(x_i)\Delta (1.101)$$
我们现在对每一个$x$进行量化，当该$x$落在第i个箱子中时，那么我们将$x_i$的值赋予这个$x$。此时，观测到$x_i$的概率为$p(x_i)\Delta$，此时我们又能得到一个离散型的概率分布，我们利用之前的方法，可以计算得到相应的entropy为：
$$H_{\Delta }=-\sum _{i}p(x_i)\Delta \text{ln}(p(x_i)\Delta )=-\sum _{i}p(x_i)\Delta \text{ln}p(x_i)-\text{ln}\Delta (1.102)$$
其中我们使用了从式(1.101)中推出的结论${\sum }_{i}p(x_i)\Delta =1$。我们此时忽略这个式子中的第二项$-\text{ln}\Delta$, 并在$\Delta \to 0$的时候，考虑第一项的极限：
$$\underset{\Delta \to 0}{\lim }\left\{\sum _{i}p(x_i)\Delta \text{ln}p(x_i)\right\}=-\int p(x)\text{ln}p(x)\text{d}x(1.103)$$
上式右侧的式子被称为differential entropy。我们可以看到，离散型和连续型变量的entropy之间差了一个量：$\text{ln}\Delta$, 这个量在$\Delta \to 0$之后会出现离散的情况。这表明，如果表达连续型随机变量的一个值将会需要大量的bits。对于一个多元随机向量$\mathbf{x}$而言，其differential entropy为：
$$H[\mathbf{x}]=-\int p(\mathbf{x})\text{ln}p(\mathbf{x})\text{d}\mathbf{x}(1.104)$$

同之前离散型随机变量一样，此时当我们得到连续型随机变量的differential entropy之后，我们可以开始考虑什么样的随机变量可以使这个entropy最大，这样一个问题。

为了使得这个$p(x)$可以得到较好的定义，我们先对它的一阶矩和二阶矩进行一定的约束，并考虑归一化条件。

因此，我们在考虑如下三个约束条件的前提下：
$${\int }_{-\infty }^{\infty }p(x)\text{d}x=1(1.105)$$
$${\int }_{-\infty }^{\infty }xp(x)\text{d}x=\mu (1.106)$$
$${\int }_{-\infty }^{\infty }(x-\mu {)}^{2}p(x)\text{d}x={\sigma }^2(1.107)$$
对这里的differential entropy进行最大化。

对于上述的等式约束优化问题，我们可以采用拉格朗日乘子的方法，最大化下面这个关于$p(x)$的泛函：
$$\begin{gathered} -{\int }_{-\infty }^{\infty }p(x)\text{ln}p(x)\text{d}x+{\lambda }_1\left({\int }_{-\infty }^{\infty }p(x)\text{d}x-1\right) \\ +{\lambda }_2\left({\int }_{-\infty }^{\infty }xp(x)\text{d}x-\mu \right)+{\lambda }_3\left({\int }_{-\infty }^{\infty }(x-\mu {)}^{2}p(x)\text{d}x-{\sigma }^2\right) \end{gathered}$$
使用变分法的方法，通过令这个泛函的变分为0的方式，我们得到如下的式子：
$$p(x)=\text{exp}\{-1+{\lambda }_1+{\lambda }_{2}x+{\lambda }_3(x-\mu {)}^2\}(1.108)$$
然后我们再通过上述的三个约束条件，将(1.108)式中的未知变量进行代入，最终得到的概率分布如下：
$$p(x)=\frac{1}{(2\pi {\sigma }^2{)}^{1/2}}\text{exp}\left\{-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right\}(1.109)$$
因此，我们得以知道，那个能使得differential entropy最大的概率分布是Gaussian分布。

此时，我们得到相应的differential entropy为：
$$H[x]=\frac{1}{2}1+\text{ln}(2\pi {\sigma }^2)(1.110)$$
此时我们可以看到，随着${\sigma }^2$的增大，这个entropy也在不断增大。
同时，不像离散型随机变量的entropy一样（非负），连续型随机变量的entropy是可以小于0的（这里当${\sigma }^2<1/(2\pi e)$时）。

假设我们有一个联合概率分布$p(\mathbf{x},\mathbf{y})$, 从中我们可以得到一个个由$\mathbf{x},\mathbf{y}$组成的对。如果我们已经知道了$\mathbf{x}$的值，那么我们获知$\mathbf{y}$的值需要额外的信息$-\text{ln}p(\mathbf{y}|\mathbf{x})$。因此平均意义上，我们获取$\mathbf{y}$所需要的额外信息为：
$$H[\mathbf{y}|\mathbf{x}]=-\int \int p(\mathbf{y},\mathbf{x})\text{ln}p(\mathbf{y}|\mathbf{x})\text{d}\mathbf{y}\text{d}\mathbf{x}(1.111)$$
这个式子被称为conditional entropy。注意，这个entropy其实考虑了所有$\mathbf{x}$的取值，对于每一个$\mathbf{x}$的取值，得到各类$\mathbf{y}$取值下信息增量的平均，然后再在$\mathbf{x}$上进行平均。

利用product rule，我们可以轻易得到以下结论：
$$H[\mathbf{x},\mathbf{y}]=H[\mathbf{y}|\mathbf{x}]+H[\mathbf{x}](1.112)$$

因此我们可以知道，用于描述$\mathbf{x}$和$\mathbf{y}$的信息，其实就等于$\mathbf{x}$单独的信息，加上在给定$\mathbf{x}$时，$\mathbf{y}$的信息。

1.6.1 Relative entropy and mutual information

本节将对之前所介绍的关于信息论中的概念，与模式识别进行联系。我们考虑到一个未知的概率分布$p(\mathbf{x})$, 并且假设我们通过另外一个概率分布$q(\mathbf{x})$来近似它。如果我们利用$q(\mathbf{x})$去对每一个状态$\mathbf{x}$进行编码，然后从sender将信息传递给receiver的话，那么由于利用概率分布$q(\mathbf{x}$（而不是真实的$p(\mathbf{x})$）而导致的信息量的增加，可以用以下式子来表达：
$$\begin{gathered} \text{KL}(p||q)=-\int p(\mathbf{x})\text{ln}q(\mathbf{x})\text{d}\mathbf{x}-\left(-\int p(\mathbf{x})\text{ln}p(\mathbf{x})\text{d}\mathbf{x}\right) \\ =-\int p(\mathbf{x})\text{ln}\left\{\frac{q(\mathbf{x})}{p(\mathbf{x})}\right\}\text{d}\mathbf{x}(1.113) \end{gathered}$$
这就是众所周知的relative entropy/Kullback-Leibler divergence(KL divergence)。我们需要注意的是，KL divergence并不是对称的，即$\text{KL}(p||q)\ne \text{KL}(q||p)$。

我们现在来证明KL divergence 是非负数，且有当且仅当$p(\mathbf{x})=q(\mathbf{x})$的时候，等号成立。为了证明这些结论，我们首先引出凸函数的定义。如果一个函数被称为“凸函数”的话，那么一定有函数里的每一个弦要么在这个函数之上，要么与函数曲线部分重合，如下图所示：

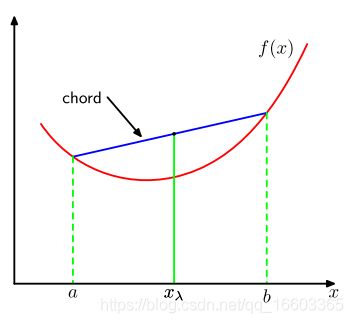
a到b区间内的任何一个点可以被写为$\lambda a+(1-\lambda )b$的形式，其中$0\le \lambda \le 1$。弦上的点表示为$\lambda f(a)+(1-\lambda )f(b)$，相应于函数上的值是$f(\lambda a+(1-\lambda )b)$。凸性表明，有：
$$f(\lambda a+(1-\lambda )b)\le \lambda f(a)+(1-\lambda )f(b)(1.114)$$
如果一个凸函数只有当$\lambda =0$和$\lambda =1$的时候，才有上面的这个等式成立，那么这样的凸函数被称为“严格的凸函数”。

如果一个函数具有相反的性质，即每一条弦都与这个函数部分重合，或在这个函数之下，那么这样的函数被称为凹函数。并且如果一个函数$f(x)$是凸函数的话，那么它的相反数$-f(x)$被称为凹函数。

利用归纳法的技巧，我们可以证明，凸函数$f(x)$满足以下不等式：
$$f\left(\sum _{i=1}^M{\lambda }_i{x}_i\right)\le \sum _{i=1}^M{\lambda }_{i}f(x_i)(1.115)$$
其中对于任意一组点$\{x_i\}$有${\lambda }_i\ge 0,{\sum }_i{\lambda }_i=1$。

式(1.115)被称为Jensen’s inequality。如果我们假设${\lambda }_i$为离散型随机变量$x$（取值为$\{x_i\}$）的概率分布的话，此时(1.115)式可以被写为：
$$f(\mathbb{E}[x])\le \mathbb{E}[f(x)](1.116)$$

对于连续型随机变量，有
$$f\left(\int \mathbf{x}p(\mathbf{x})\text{d}\mathbf{x}\right)\le \int f(\mathbf{x})p(\mathbf{x})\text{d}\mathbf{x}(1.117)$$

我们将Jensen’s inequality 应用在KL divergence上，有：
$$\text{KL}(p||q)=-\int p(\mathbf{x})\text{ln}\left\{\frac{q(\mathbf{x})}{p(\mathbf{x})}\right\}\text{d}\mathbf{x}\ge -\text{ln}\int q(\mathbf{x})\text{d}\mathbf{x}=0(1.118)$$
其中，我们利用了条件：$-\text{ln}x$是一个严格的凸函数，因此，我们知道当且仅当$q(\mathbf{x})=p(\mathbf{x})$时，这个等式才能满足。因此我们可以利用KL divergence来度量两个概率分布之间的不相似程度。

我们可以从数据压缩和密度估计的角度来对这里的一些性质进行分析。因为最有效的数据压缩方法是利用该数据真实的分布进行编码，因此我们利用任何其他的分布，对该数据进行编码的时候，都会遇到冗余的问题，此时我们编码的平均码长必然是大于或等于利用该数据本身进行编码的。因此，就自然有KL divergence是大于等于0的。

假设真实的数据来源于一个未知的概率分布$p(\mathbf{x})$, 我们希望利用$q(\mathbf{x}|\theta )$来对这个概率分布进行近似。这个q概率分布函数是一个已知的函数（例如多元高斯分布），它受到了可调参数$\theta$的影响。一种确定参数$\theta$的方式是通过调节$\theta$最小化$p(\mathbf{x})$与$q(\mathbf{x}|\theta )$之间的KL divergence。而由于我们一般并不知道$p(\mathbf{x})$本身的缘故，我们无法直接对这个KL divergence进行计算。但是，由于我们的training set中的data points ${\mathbf{x}}_n,n=1,...,N$是从$p(\mathbf{x})$中采样出来的点，因此我们可以通过下式来估计KL divergence：
$$\text{KL}(p||q)\simeq \sum _{n=1}^N\{-\text{ln}q({\mathbf{x}}_n|\theta )+\text{ln}p({\mathbf{x}}_n)\}(1.119)$$
在这个式子中，第二部分与$\theta$无关，第一部分是关于$\theta$在training set下的负对数似然函数。因此，此时最小化KL divergence等价于最大化似然函数。

我们最后来讨论一下$p(\mathbf{x},\mathbf{y})$与$p(\mathbf{x})p(\mathbf{y})$之间的KL divergence，我们用这样一种度量方式，来衡量两个随机变量距离它们之间相互独立，还有多远：
$$\begin{gathered} I[\mathbf{x},\mathbf{y}]\equiv \text{KL}(p(\mathbf{x},\mathbf{y})||p(\mathbf{x})p(\mathbf{y})) \\ =-\int \int p(\mathbf{x},\mathbf{y})\text{ln}\left(\frac{p(\mathbf{x})p(\mathbf{y})}{p(\mathbf{x},\mathbf{y})}\right)\text{d}\mathbf{x}\text{d}\mathbf{y}(1.120) \end{gathered}$$
上式被称为变量$\mathbf{x}$和$\mathbf{y}$之间的“互信息”。从KL divergence的性质中，我们可以得知，$I(\mathbf{x},\mathbf{y})\ge 0$，等号成立的条件为，$\mathbf{x}$和$\mathbf{y}$之间相互独立。

再利用sum rule 和 product rule, 我们可以得到互信息与条件熵之间的关系：
$$I[\mathbf{x},\mathbf{y}]=H[\mathbf{x}]-H[\mathbf{x}|\mathbf{y}]=H[\mathbf{y}]-H[\mathbf{y}|\mathbf{x}](1.121)$$

因此，我们可以将互信息看作是在知道$\mathbf{y}$之后，关于$\mathbf{x}$信息的uncertainty的减少量（反之亦然）。从贝叶斯的观点来看，我们可以将$p(\mathbf{x})$看作$\mathbf{x}$的先验，并且将$p(\mathbf{x}|\mathbf{y})$看作我们观察新数据$\mathbf{y}$之后的后验。因此互信息表示我们在观察到新的$\mathbf{y}$之后，对$\mathbf{x}$的不确定程度的减少量。