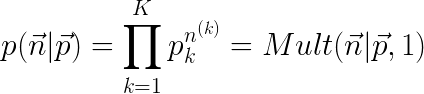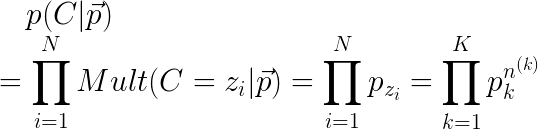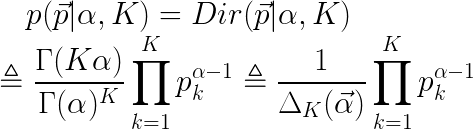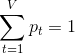《Parameter estimation for text analysis》阅读笔记（三）

本文内容为Parameter estimation for text analysis阅读笔记第三篇，如有错误或疏漏之处，恳请各位批评指正！

简介：

虽然贝叶斯模型的计算往往非常棘手（evidence往往难以求得），但由于我们可以自由选择我们的先验（prior belief），我们往往采用共轭先验分布（conjugate prior distributions）。

1. 共轭（Conjugacy）

假设是的共轭先验，那么在Bayes's rule中，后验函数 和先验函数 往往具有相同的形式(同时Bayes' rule中的分母计算也较为简单)，并且后验将在先验的基础上通过参数化(parameterization)的方式将观测数据包含在后验分布的参数中。除此之外，共轭的方法同样也会给hyperparameter一种较好的解释。在原文中给出的例子里，后验可以被视作先验中的超参数（作为伪计数（pseudo counts））与观测数据计数 的结合。

共轭先验-似然函数对使得我们可以通过marginalise的方法消去observations中的likelihood的参数，转而直接使用hyperparameters来描述observations的分布函数。以该文中的例子进行解释：

由最终的式子可以看出，在利用共轭先验的情况下，我们可以仅仅利用hyperparameters来表示observations的分布，从而绕开了计算似然函数的参数p时所可能遇到的问题。换句话说，当利用共轭分布时，分母难以计算的问题被解决了。因此，我们可以仅仅根据prior和observations来对未来出现的（Bernoulli）实验结果进行预测，即：

由上式可以发现，此处我们没有对参数p进行任何估计，也就是说，我们直接跨过了参数估计这一步，同样是利用Bayesian inference的方法，但通过公式推导避开了可能需要进行计算的参数，而直接通过Bayes' rule，利用observations和prior对可能遇到的新数据进行了预测，相当于是对Bayesian inference的一种简化。这是共轭先验-似然函数对的优势。

此处我们引入binomial distribution，它描述的是：假设我们的N次Bernoulli实验中，有次是正面朝上的（并不知道是哪次），那么在这么多次实验下，该硬币正面朝上的概率为p的可能性有多大：

同Bernoulli 分布一样，binomial分布的共轭先验也是Beta分布。需要注意的一点是，由于我们只知道统计后的频率结果，也即只知道其中有次是硬币朝上的情况，因此我们要考虑所有可能导致“次是硬币朝上”的结果出现的实验，这样的实验数量可以通过组合数的计算得到，因此该分布会有一个因子是。

2. 多变量的情况

如果我们考虑Bernoulli实验的结果不止2种，而是有K种，那么我们就会得到一个K维的Bernoulli实验（multinomial experiement），就像是在掷骰子。如果我们重复进行该实验，即可得到一个关于观测事件（observed events）的多项式分布，该分布是binomial distribution的generalize：

其中，和满足和。

而一个单独的multinomial trial将Bernoulli distribution generalizes到一个discrete categorical distribution上：

其中只有在被选到的那个event z上的值为1，其余地方的值均为0，因此我们可以将上式进行简化：

此时引入一个多项式随机变量C。当对该multinomial experiment重复N次后，该随机变量C的likelihood函数为：

需要注意的是，不同于binomial generalizes出来的multinomial distribution，这里的distribution并没有加系数，因为这里的概率表示的是某一个特定的N次multinomial experiment得出来的结果，而非在某一种统计结果下，各种实验可能性之和。换句话说，这里每一次sample出来的都是不一样的随机变量的取值，这些随机变量间是i.i.d的，且这些随机变量都仅含一次K维的Bernoulli experiment。而刚才出现组合数的概率分布式中，我们只有唯一的一个随机变量，但这个随机变量包含了多次K维的Bernoulli experiments。所以说，这个乘积（likelihood）并不是multinomial distribution，而是说这个乘积中的每一项都是Multinomial的。

对于上式所示的likelihood，由于其中的乘积项服从multinomial distribution，所以我们可以用该distribution的共轭先验Dirichlet distribution，来对参数的分布进行设定。

Dirichlet函数是Beta函数在多维度上的generalize，其表示形式如下：

在Dirichlet distribution中，有一类特殊的Dirichlet distribution，被称为symmetric Dirichlet distribution，此时的参数将由标量替代。假设我们的参数有K维的话，那么此时有p的先验分布函数：

其中，。

3. 文本建模

从此处开始，我们将讨论文本建模中的内容。假设我们所能观察到的文字串为, 其中包含了N个独立同分布的文字，它们都是从一个随机变量W中sample出来的（类比于上一节中的“多项式随机变量C”）。我们同时也可以将这样sample出来的文字看作是从一个大小为V的词表（类比于event z）中sample出来的。这样sample出来的N个单词的likelihood可以表示为：

其中，且。

类比于上一节所述的multinomial distribution公式的变换，我们不难得知，这里sample出来的每一个单词同样也服从multinomial distribution。通过这个likelihood公式，我们可以估计出一组的值，因此，这里进行参数估计的前提是：在整个corpus中的所有单词，都统一是从同一个multinomial distribution中sample出来的（也即的值唯一）。

我们将这种模型称为“unigram model”。在unigram模型中，它所做出的假设是，在整个corpus上，likelihood函数是唯一的，也即中的是fix住的 (可能有人会问：为什么是fix住的？那用来解释的话，不应该是变量？首先我们要清楚，likelihood函数中，当作为变量时，是因为我们要对进行估计。就好比说一个线性模型公式中，它的每一个变量都带有一个系数，但只有当我们在估计这些系数的时候，这些系数()才是“变量”，这些变量()才是“常数”，除此之外，正常情况下，当这些系数固定时，自然这个线性模型就定型了，自然就成了唯一的了。而当我们得到了两组不同的系数时，才可以说，我们有两个不同的线性模型。同样，当我们只会得到唯一一组时，我们的likelihood函数就是唯一的)。

这样的模型有一个问题：在一个corpus中，我们的document往往不只有一个，而对于不同的document，如果它们所描述的内容本身就大相径庭，那么这些documents的单词的分布自然差异较大，此时它们共有同一组就显然是一种不合理的假设。

正如在第（二）节所讲的顺序那样，此时我们不再只单纯关注一个likelihood，而是同时引入关于参数的先验。那么这个参数的先验应该长什么样子呢？联想到共轭先验分布的一些优良性质，此时我们尝试采用Dirichlet distribution，并假设是服从这个分布的：。可能此时有人会想着，接下来就可以求MAP了。可以是可以，但既然有了共轭先验，我们求Bayes' rule中的分母就变得容易多了，因此我们完全有能力将后验分布的整个表达式求出来（等有了后验表达式后，MAP就可以很轻易地根据概率密度最大值求得）：

（没理解这里）这种参数更新的方式被称为：，即我们有一个缸(urn)， 里面装有V种颜色的W个小球，我们每次从中sample出一个小球，观察它的颜色，然后将它放回，并同时给urn中再放一个一模一样的小球。所以urn中的小球数量是增加的。作者说，这里的Dirichlet所呈现的是一种“rich get richer”（或者可以说是clustering）的动作。

（个人理解）类比于文本建模，

显然，固定一个参数, 然后对生成文本的概率进行计算（unigram）是有许多问题的，所以我们希望能够直接通过我们所得到的observations和prior，来直接对生成文本的概率进行计算。此时我们可以通过利用Dirichlet distribution中的hyperparameter(伪计数)以及marginalizing掉参数的方法来实现我们的目标：

由于参数具有约束条件, 因此该参数所在的范围是embeds在K维空间中的一个K-1维的单纯形，这个单纯形由所有的点连线所形成，如下图所示：

所以我们继续推导上面的公式：

与的求解类似，通过上式对文本分布的建模，我们只需要得知先验分布的参数和observations的信息，而在避开似然函数参数的求解的前提下，即计算得到文本概率分布公式。