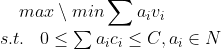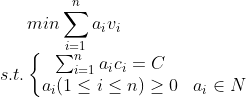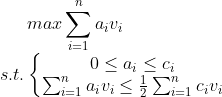动态规划之01背包问题（Knapsacks Problem）

        01背包问题：给定n种物品和一个容量有限的背包，每件物品都会消耗背包的一定容积，并带来一定价值，要求如何选取装入背包中的物品，使得背包内的物品价值最大。

01背包使用动态规划解决的具体分析思路不讲了，详细可以参考《背包九讲》。下面只写写HDU几道题目的解题报告。

一、基本01背包问题

这类问题的特点是：每件物品的数量是一个，要么放一个，要么一个不放，且背包的容量是整形数。

题目：HDU 1203， 大意是用一定数量的前申请不同学校的offer，每所学校要花一定的申请费用，且只有一定的概率才能申请到offer，求怎么分配这笔钱，才能使得至少拿到一个offer的概率最大。初始金钱不一定要花完。

这题比较容易看出是01背包问题，背包是初始的金钱，物品是学校，物品的消耗是申请费用，物品的价值是概率。由于题目求的是至少拿到一个offer的概率，相互独立事件求至少一件发生的概率一般反过来较为简单，所以可以考虑实现时将一个offer也拿不到的概率作为价值，要求在有限背包容量下，这个价值最小。下面是AC的代码：

#include 
#include 
#define Max 10001
using namespace std;
float min(float a, float b)
{
   return a>b?b:a;   
}
int main()
{
    int n,m;
    while(cin>>n>>m && (n || m)  )
    {
        float* dp = new float[n+1];
        int* cost = new int[m];
        float* value = new float[m];            
        for(int i = 0 ; i < m ; i++)
        {
            int c;
            float v;
            cin>>c>>v;
            cost[i] = c;
            value[i] = 1-v;  //存储的是申请不上的概率      
        }                
        for(int i = 0 ; i < n+1 ; i++) dp[i] = 1;
        for(int i = 0 ; i < m ; i++)
        {
            for(int j = n ; j >= cost[i] ; j--)
            {
                dp[j] = min(dp[j], dp[j-cost[i]]*value[i]);        
            }        
        }
        dp[n] = 100*(1-dp[n]);
        cout<

题目：HDU 2602， 更简单的01背包问题了。

01背包事实上可以从数学规划的角度来进行理解。所谓01背包问题，实际上就是求如下的数学规划问题：

其中，  是物品提供的价值，  是物品的消耗， C是物品的总消耗，也即背包的容量。

二、完全背包问题

问题特点：每件物品的数量有无限多个，可以一个不放，也可以放任意数量的，背包容量为整形数。

题目：HDU 1114， 大意是有一个存钱罐，已知存钱罐中硬币的重量和每种面值硬币的重量，求存钱罐中最少有多少钱。

这是完全背包问题，因为每种面值的硬币并不限数量，可以有任意个，只要背包容量允许。在本题中，背包的容量是硬币的总重量，物品是硬币，物品的消耗是每种硬币的重量，物品的价值是硬币的面值，要求在消耗完总重量的前提下，物品的价值最小。因为必须消耗完背包的容量，所以在初始化时需要做点不同的工作。AC代码如下：

#include 
#define Inf 99999999
using namespace std;

int min(int a, int b)
{
    return a>b?b:a;   
}

int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        int e, f, n;
        cin>>e>>f; cin>>n;
        int vol = f - e;//存钱罐中硬币总重量
        int* value = new int[n];//硬币面值
        int* weight = new int[n];//硬币重量
        for(int i = 0 ; i < n ;i++) cin>>value[i]>>weight[i];
        int* dp = new int[vol+1];
        dp[0] = 0;//当背包容量为0时，合理的解是硬币价值为0
        for(int i = 1 ; i < vol+1 ; i++) dp[i] = Inf; //注意这里的初始化，Inf表示没有满足消耗完背包容量的解
        for(int i = 0 ; i < n; i++)
        {
           for(int j = weight[i] ; j < vol+1 ; j++)
               dp[j] = min(dp[j], dp[j-weight[i]]+value[i]);        
        }     
        if(dp[vol] == Inf) cout<<"This is impossible."<

这题虽然是完全背包问题，不过从数学规划的角度来理解的话，可能会有助于对背包也形成更好的理解。

设硬币的面值是  ， 单个硬币的重量分别是，存钱罐中所有硬币的重量是， 则所求问题可以总结为如下的整数规划问题：

将背包问题理解为数学规划可能会有助于对某些问题的理解。

三、多重背包问题

多重背包问题的特点是，每件物品的数量不是只有一件，也不是有无限件，而是有一定的数量。

如果直接穷举每件物品的数量，时间复杂度会非常高，所以常用的方法是二进制优化和单调队列优化。单调队列优化的时间复杂度接近普通01背包的时间复杂度，不过实现起来比较麻烦，暂时不讲，可以参考这篇文献。

（1）二进制优化

二进制优化的思想如下。假设物品  的数量是  ，每件该物品的消耗量是   ， 那么将该物品拆分成如下几个消耗量的物品：  ， 其中 ， 注意最后的  可能不是2的倍数，因为 可能不是2的幂数。这样拆分的原因是 1、2、4、8、....等数的或取或不取的组合，即  恰好能穷尽  的所有整数。用集合来表示就是 ， 但是拆分成的物品数却从原来的  减少到， 由此可以极大的提高算法的效率。下面还是在题目中看具体实现。

题目：HDU 2191 ， 大意是已知一定数额的初始经费和大米的种类，以及每种大米的每袋的价格、重量和袋数。求在给定经费下，最多买多重的大米。

在这道题中，背包的容量是初始经费，物品的每袋大米，物品的消耗是每袋大米的价格，物品的价值是每袋大米的重量，物品的限定数量是袋数。理清关系后，不难写出代码。下面是我的AC代码：

//multi knapsack problem, hdu 2191
#include 
using namespace std;

int main()
{
    int C;
    cin>>C;
    while(C--)
    {
       int n,m;
       cin>>n>>m;
       int* cost = new int[m];
       int* value = new int[m];
       int* count = new int[m];
       for(int i = 0 ; i < m ;i++) cin>>cost[i]>>value[i]>>count[i];
       // multi knapsack problem
       int* dp = new int[n+1];
       for(int i = 0 ; i <= n; i++) dp[i] = 0;
       for(int i = 0 ; i < m ; i++)
       {
             if(cost[i]*count[i] >= n)//完全背包
             {
                   for(int j = cost[i] ; j <= n ; j++)              
                       dp[j] = max(dp[j], dp[j-cost[i]]+value[i]);
             }
             else//01背包
             {
                   int k = 1;
                   while(k < count[i])
                   {
                      for(int j = n ; j >= k*cost[i] ; j--)
                           dp[j] = max(dp[j], dp[j-k*cost[i]]+k*value[i]);
                      count[i] -= k;
                      k <<= 1;            
                   }
                   for(int j = n ; j >= count[i]*cost[i] ; j--)
                      dp[j] = max(dp[j], dp[j-count[i]*cost[i]]+count[i]*value[i]);                 
             }                           
       }
       cout<

这题从数学规划的角度来考虑，就是如下方程：

其中， 是每种大米的重量（即物品的价值），  是每种大米的价格（即物品的消耗），  是每种大米的数量（即物品的限制）， C是总资金。

题目：HDU 1171 ，大意是给定N种物品，每种物品有一个价值和固定的数量，要求将这么多物品均分成两部分，使得两部分的价值之差尽可能小，且第一个部分的价值不小于第二部分的价值。

这题粗看之下很容易发现是01背包问题，但是再看看又会觉得棘手，因为根据题目没有明显的背包这个概念。不知道以什么作为背包。但如果用数学规划的角度来看的话，就比较简单。

首先，我们记得基本多重背包问题的数学规划形式如上。

其次，列出本题的数学规划形式如下：

最后，类比前后两种数学规划公示，发现如果将  作为背包，则该问题可以用完全背包的方法解决。下面是AC的代码：

//hdu 1171, dynamic programming
//背包容量定义为总和的一半 
#include 
#include 

using namespace std;

int v[52];
int m[52];
int f[155002];
int n,total,half;
    
void ZeroOnePake(int v)
{
    for(int i=half;i>=v;i--)
        f[i]=max(f[i],f[i-v]+v);
}

void CompletePake(int v)
{
    for(int i=v;i<=half;i++)
        f[i]=max(f[i],f[i-v]+v);
}
                  
void MultiPack(int v,int m)  
{
    if(v*m>=half){CompletePake(v);return;}
    int k=1;
    while(k=0)
    {
        if(n==0){printf("0 0\n");continue;}
        total=0;
        for(int i=1;i<=n;i++)
        {
            scanf("%d%d",&v[i],&m[i]);
            total+=v[i]*m[i];
        }
        half=total/2;
        for(int i=0;i<=total;i++) f[i]=0;
        for(int i=1;i<=n;i++)   MultiPack(v[i],m[i]);
        printf("%d %d\n",total-f[half],f[half]);
    }                                          
    return 0;
}

（2）单调队列优化

单调队列优化的方法参考上面给出的文献。以后有空可能会来谈谈。

四、二维费用背包问题

所谓二维费用背包问题是指每件物品具有两种不同的费用，选择物品的时候要同时付出两种费用。二维费用背包问题的递推公式，参考《背包九讲》的内容，给出如下：

题目：HDU 2159 ， 大意是一个人在游戏中打怪升级，为了升级需要一定经验，因此需要杀怪，每杀一个怪会得到一定经验，但同时会消耗这个人对游戏的忍耐度，而人的忍耐度是有限的，超过了忍耐度，人就不再玩这款游戏。另一方面，这个人设定了最大杀怪数，杀怪数超过多少时就不再玩这款游戏了。求这个人能否在杀怪数满足要求和忍耐度不低于0之前完成升级任务。

首先，按照背包问题一般的解决思路，先给出各个参数。背包是忍耐度和最大杀怪数，物品是怪物，物品的消耗是忍耐度和怪物数（每次1个），物品的价值是杀怪所得经验。

有了上述的抽象，不难给出下面的AC代码：

#include 
#define Max 101
using namespace std;
int max(int a, int b)
{
   return a>b?a:b;   
}
int dp[Max][Max];
int main()
{
    int n,m,k,s;
    while(cin>>n>>m>>k>>s)
    {
        int* cost = new int[k];
        int* value = new int[k];
        for(int i = 0  ; i < k ; i++) cin>>value[i]>>cost[i];
        for(int i = 0 ; i < m+1 ; i++)
           for(int j = 0 ; j < s+1 ; j++) dp[i][j] = 0;
        for(int i = 0 ; i < k ; i++)
        {
            for(int j = cost[i] ; j < m+1 ; j++)
            { 
                 for(int t = 1 ; t < s+1 ; t++)
                     dp[j][t] = max(dp[j][t], dp[j-cost[i]][t-1]+value[i]);
            }             
        }  

        bool flag = true;
        int i,j;
        for( i = 0 ; i < m+1 && flag ; i++)
        {
          for( j = 0 ; j < s+1 && flag; j++)
            if(dp[i][j] >= n){flag = false;break;}
          if(!flag) break;
        }  
        cout<

同上，我们还想给出二维背包问题的数学规划形式。

各个符号的含义：a表示每件物品的放入数量，v是每件物品的价值， 是每件物品的第一维消耗， 是每件物品的第二维消耗，  是背包的第一维容量，  是背包的第二维容量。

五、连续值背包问题

问题特征：背包的容量不是离散的整型值，而是浮点型数值。

问题：HDU 2955， 大意是一个强盗想要抢劫几家银行，每家银行有一定的存款数，且每抢劫一家银行都有一定概率被抓获，问在给定的安全概率下，强盗所能抢劫到的最大钱数。且抢劫各个银行被抓的概率是相互独立的。

首先要按背包问题的术语来进行抽象，背包显然是安全概率（浮点数），物品是银行，物品的消耗是抢劫该银行并且安全逃脱的概率（浮点数）， 物品的价值是银行的存款。

看起来是个01背包问题，但是因为背包容量是离散值而变得有点棘手。事实上用回溯法或者分支界限法这类对背包容量数据类型要求比较小的算法可以解决此类问题，如果用01背包的思想来解决，就需要对背包过程做进一步的抽象。

首先写出背包问题最初始的递推公式：

显然， 是一个阶梯函数，而且该阶梯函数在数轴上的图形是由其跳跃点对  唯一确定的。如此，求原问题的背包问题就转化为求其在数轴上的图形的问题，进而转化为求其跳跃点对的问题。为此可以给出如下算法：

算法1：

（1）输入物品的消耗 （浮点型）， 物品的价值 ， 背包的总容量 （浮点型）

（2）初始化跳跃点集 

（3）对每一件物品 ，设当前跳跃点集为，且中的点按第一元素的升序排列。按如下方法生成 

      （4）对每一个 ， 令 ， 如果 ， 则将 添加到 中；否则，回到步骤（3）

      （5）令

      （6）对任意的，如果 ， 且 ，则称点 覆盖 点， 此时从点集 中删除点

      （7）在上述过程中，保证也是按第一元素的升序排列

（8）输出中的最后一个元素，即是所求的最大的物品价值

算法的正确性可以参考王晓东《计算机算法设计与分析（第3版）》相关章节，其时间复杂度是，其中c是背包总容量，n是物品的数量。

按照上面所言的算法，给出HDU 2955的AC代码如下：

#include 

using namespace std;
#define MaxN 101
#define MaxNode 6000       
int value[MaxN];//money
double cost[MaxN];//probability
struct node{
      double x;  
      int y;
}JumpNode[MaxNode];

int Knapsack(int n, float pMax )
{
   JumpNode[0].x = 0 ;
   JumpNode[0].y = 0 ;
   int left = 0, right = 0, next = 1;
   int* head = new int[n+2];
   int* rx = new int[n+2];
   head[n] = 1;
   for(int i = n ; i >= 1 ; i--)
   {
      int k = left;     
      for(int j = left ; j <= right ; j++)
      {   
          double x = JumpNode[j].x + cost[i] - JumpNode[j].x * cost[i];
          if( x > pMax ) break;
          int y = JumpNode[j].y + value[i];  
          while(k<=right && JumpNode[k].x < x)
          {
               JumpNode[next].x = JumpNode[k].x ;
               JumpNode[next++].y = JumpNode[k++].y;
          }
          if(k<= right && JumpNode[k].x == x)
          {
               if(y < JumpNode[k].y ) y = JumpNode[k].y;
               k++;       
          }        
          if(y > JumpNode[next-1].y)
          {
               JumpNode[next].x = x;
               JumpNode[next++].y = y;
          }
          while(k<=right && JumpNode[k].y <= JumpNode[next-1].y) k++;  
      }
      while(k <= right)
      {
          JumpNode[next].x = JumpNode[k].x;
          JumpNode[next++].y = JumpNode[k++].y;
      }
      left = right+1;
      right = next-1;
      k = left;
      next = 1;
      while(k<=right)
      {
          JumpNode[next].x = JumpNode[k].x;
          JumpNode[next++].y = JumpNode[k++].y;       
      }
      left = 1;
      right = next - 1;         
    }   
    return JumpNode[next-1].y ;           
}

int main()
{
    int T;
    cin>>T;
    while(T--)
    {
       float pMax;
       int n;
       //memset(JumpNode, 0, MaxNode*sizeof(JumpNode));
       cin>>pMax>>n;
       
       for(int i = 1 ; i <= n; i++) cin>>value[i]>>cost[i];
       for(int i = 0 ; i < MaxNode ; i++) JumpNode[i].x = 0, JumpNode[0].y = 0 ;
       cout<

注意这一行代码

double x = JumpNode[j].x + cost[i] - JumpNode[j].x * cost[i];

这样写的原因是假设抢劫a银行（a银行可能是一个银行，也可能是很多个银行）被抓的概率是， 抢劫b银行被抓的概率是， 则抢劫a银行和b银行，被抓的概率是

另外，下面代码

  k = left;
      next = 1;
      while(k<=right)
      {
          JumpNode[next].x = JumpNode[k].x;
          JumpNode[next++].y = JumpNode[k++].y;       
      }
      left = 1;
      right = next - 1;    

这段代码的目的是每生成了新的跳跃点集，则整体左移，覆盖掉原来的跳跃点集。如果要输出被选中的背包，则保留原来的跳跃点集是有用的，但是只输出最大价值时，原来的跳跃点集是没有用的。那为什么还要花时间覆盖掉原来的 呢？因为稍微一分析就可以发现，所有物品生成的跳跃点集的元素总数目会非常大，当N=100时，M=6000都不够，所以为了节省内存空间，采用移动的方法覆盖掉原来的跳跃点集。

此外，这题还有一种解法，将所有银行的金钱总数当成背包容量，则物品是银行，物品的消耗是银行的金钱数量，物品的价值是被抓概率。目标是被抓概率的最小化。当然，有两点需要注意：第一就是并非所有容量的背包是有意义的，因为将银行的金钱总和看成背包容量时，有些容量是不能用银行的金钱数表示的。因此，初始化阶段要做一些特殊的工作。第二就是背包容量满时，不一定是满足题目要求的概率，需要从右往左找到被抓概率第一次满足安全概率时的背包容量。
具体的分析就不讲了，贴一下别人的AC的代码。

#include
#include
#include
#define MAXN 101
#define MAXV 10001

using namespace std;

int cost[MAXN];
double weight[MAXV],d[MAXV];

int main()
{
    int test,sumv,n,i,j;
    double P;
    cin>>test;
    while(test--)
    {
        scanf("%lf %d",&P,&n);
        P=1-P;
        sumv=0;
        for(i=0;i=cost[i];j--)
            {
                d[j]=max(d[j],d[j-cost[i]]*weight[i]);
            }
        }
        bool flag=false;
        for(i=sumv;i>=0;i--)
        {
            if(d[i]-P>0.000000001)
            {
                printf("%d\n",i);
                break;
            }
        }
    }
    return 0;
}