全连接的神经网络Java实现
前言
本例程实现了一个最简的,支持自定义层数和每一层神经元个数的 全连接前馈神经网络。其实,它就是一般教课书里面入门的一种人工神经网络。本例程具有以下自特点:
- 实现了反向传播(BP)算法
- 实现了随机梯度下降(SGD)算法
- 全部神经元使用sigmoid激活函数
经过实验,我发现,在没有任何优化的网络结构上(本例的结构)不适合使用类似relu的激活函数,因为它对输入的数据范围不加限制,会造成优化过程中出现 NaN、Infinite值。
原理
参见 邱锡鹏 《神经网络与深度学习》 https://github.com/nndl/nndl.github.io
代码
先定义一个抽象的接口。这仅仅演示了作为一个模型所应该具有的基本功能。如果是实际要实现一个机器学习框架,如此设计确实存在不合理的地方。
package com.cloudea.ANN;
public abstract class Model {
public abstract void fit(double[] x, double[] y, double alpha); //训练,其中alpha是学习率
public abstract double[] predict(double[] x); //预测
public abstract void load();
public abstract void save();
}
然后实现代码。
package com.cloudea.ANN;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Random;
public class DNN extends Model {
private List<Integer> layers = new LinkedList<>(); //各层所拥有的神经元个数
private List<double[][]> matrixes = new LinkedList<>(); //各层的参数矩阵,包括权重参数和截距项
private Random random = new Random(); //用于随机初始化参数
/* 训练一次
x - 输入向量
y - 输出向量
alpha - 学习率
*/
@Override
public void fit(double[] x, double[] y, double alpha) {
if(layers.size() == 0 || layers.size() == 1) return;
if(x.length != layers.get(0)) return;
if(y.length != layers.get(layers.size() - 1)) return;
//前向传播
List<double[]> results = __predict(x);
double[] err = new double[y.length];
double[] y_pre = results.get(results.size() - 1);
for(int i = 0; i < y_pre.length; i++){
err[i] = Math.pow(y_pre[i] - y[i], 1);
}
//反向传播
double[][] errs = new double[matrixes.size() + 1][];
errs[matrixes.size()] = err;
for(int i = matrixes.size() - 1; i >= 0; i--){
double[] z = results.get(i * 2 + 1);
errs[i] = new double[z.length];
for(int j = 0; j < errs[i].length; j++){
errs[i][j] = 0;
if(i != matrixes.size() - 1){
double[][] matrix = matrixes.get(i + 1);
for(int k = 0; k < errs[i+1].length; k++){
errs[i][j] += matrix[k][j];
}
}else {
errs[i][j] = 2 * errs[i+1][j];
}
double l = logistic(z[j]);
errs[i][j] *= l * (1 - l);
}
}
//参数更新(梯度下降一次)
for(int i = matrixes.size() - 1; i >= 0; i--){
double[][] matrix = matrixes.get(i);
double[] a = results.get(i * 2);
for(int j = 0; j < matrix.length; j++){
for(int k = 0; k < matrix[j].length; k++){
if(k == matrix[j].length - 1){
matrix[j][k] -= alpha * errs[i][j];
}else {
matrix[j][k] -= alpha * errs[i][j] * a[k];
}
}
}
}
}
/* 批量训练
xs - x向量数组,xs[0]表示第一个向量
ys - y向量的数组,ys[0]表示第一个向量
timesFit - 随机迭代次数
alpha - 固定的学习率
*/
public void fit(double[][] xs, double[][] ys, int timesFit, double alpha){
if(xs.length != ys.length) return;
//SGD
for(int i = 0; i < timesFit; i++){
int index = random.nextInt(xs.length);
fit(xs[index], ys[index], alpha);
}
}
@Override
public double[] predict(double[] x) {
List<double[]> results = __predict(x);
return results.get(results.size() - 1);
}
/* 内部的前向传播
x - 输入向量
返回值一个向量列表,形如:
[ 第1层净输入,
第1层输出,
第2层净输入,
第2层输出,
.....,
最后层净输入,
最后层输出,
]
所谓“净输入”,即经过线性变换后,输入到激活函数中的值。
所谓“输出”,即经过激活函数之后得到的值。
*/
private List<double[]> __predict(double[] x){
ArrayList<double[]> results = new ArrayList<>();
results.add(x);
if(layers.size() == 0 || layers.size() == 1 || x.length != layers.get(0)){
return results;
};
for(int i = 1; i < layers.size() ; i++){
double[] z = new double[layers.get(i)];
double[] a = new double[layers.get(i)];
for(int j = 0; j < z.length; j++){
double zj = 0;
double[][] matrix = matrixes.get(i - 1);
for(int k = 0; k < layers.get(i - 1); k++){
zj += matrix[j][k] * x[k];
}
zj += matrix[j][matrix[j].length - 1];
z[j] = zj;
a[j] = logistic(zj);
}
results.add(z);
results.add(a);
x = a;
}
return results;
}
@Override
public void load() {
}
@Override
public void save() {
}
/* 增加一层神经元
numCeils - 神经元个数
*/
public void addLayer(int numCeils){
if(numCeils > 0){
layers.add(numCeils);
if(layers.size() > 1){
int rows = layers.get(layers.size() - 1);
int cols = layers.get(layers.size() - 2);
double[][] matrix = new double[rows][];
for(int i = 0; i < rows; i++){
matrix[i] = new double[cols + 1]; // 之所以加1,是为了把偏置单元的参数也存在一起
for(int j = 0; j < matrix[i].length; j++){
matrix[i][j] = random.nextDouble() * 2;
}
}
matrixes.add(matrix);
}
}
}
/* 增加多层神经元
numCeils - 每层神经元个数
count - 层数
*/
public void addLayers(int numCeils, int count){
if(numCeils > 0){
for(int i = 0; i < count; i++) {
addLayer(numCeils);
}
}
}
/*sigmoid函数*/
public static double logistic(double x){
return 1 / (1 + Math.exp(- x));
}
}
测试
我们使用以上模型对以下函数进行拟合:
f ( x , y , z ) = x 2 + y 2 + z 2 f ( x , y , z ) = x + y + z f ( x , y , z ) = x ⋅ y ⋅ z \begin{aligned} f(x, y, z) &= \sqrt{x^2+y^2+z^2} \\ f(x,y,z)&=x+y+z \\ f(x,y,z)&=x\cdot y\cdot z \end{aligned} f(x,y,z)f(x,y,z)f(x,y,z)=x2+y2+z2=x+y+z=x⋅y⋅z
测试代码如下:
package com.cloudea.ANN.test
import com.cloudea.ANN.DNN;
import com.cloudea.ANN.Model;
import org.junit.Test;
import java.util.Random;
public class TestDNN {
@Test
public void test(){
DNN dnn = new DNN();
dnn.addLayer(3);
dnn.addLayer(5);
dnn.addLayer(7);
dnn.addLayer(3);
//产生虚拟数据
Random random = new Random();
double[][] xs = new double[100][];
double[][] ys = new double[100][];
for(int i = 0; i < xs.length; i++){
xs[i] = new double[3];
ys[i] = new double[3];
xs[i][0] = random.nextDouble();
xs[i][1] = random.nextDouble();
xs[i][2] = random.nextDouble();
ys[i][0] = f1(xs[i][0],xs[i][1],xs[i][2]);
ys[i][1] = f2(xs[i][0],xs[i][1],xs[i][2]);
ys[i][2] = f3(xs[i][0],xs[i][1],xs[i][2]);
}
//train
dnn.fit(xs, ys, 1000000, 0.001);
//使用
double[] y = dnn.predict(new double[]{1,0.2,0.3});
for(int i = 0; i < y.length; i++){
System.out.print(y[i] + " ");
}
System.out.println();
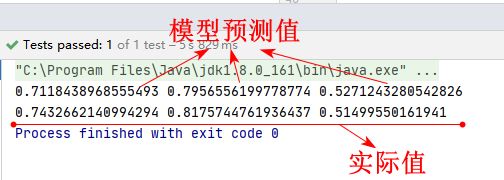
double[] y_true = {f1(1,0.2,0.3), f2(1,0.2,0.3), f3(1,0.2,0.3)};
for (int i = 0; i < y_true.length; i++){
System.out.print(y_true[i] + " ");
}
}
double f1(double x, double y, double z){
return DNN.logistic(Math.sqrt(x * x + y*y + z * z));
}
double f2(double x, double y, double z){
return DNN.logistic(x + y + z) ;
}
double f3(double x, double y, double z){
return DNN.logistic(x * y * z) ;
}
}