【Leetcode】Weekly 202

Leetcode 第202场周赛

这一次是三七互娱周赛，前段时间好久没打了，今天回来打了一把，感觉还行，整体题目比较简单，打了个40名，但是还是有失误，本可以更好。

存在连续三个奇数的数组

给你一个整数数组 arr，请你判断数组中是否存在连续三个元素都是奇数的情况：如果存在，请返回 true ；否则，返回 false 。

示例1:

输入：arr = [2,6,4,1]
输出：false
解释：不存在连续三个元素都是奇数的情况。

示例2:

输入：arr = [1,2,34,3,4,5,7,23,12]
输出：true
解释：存在连续三个元素都是奇数的情况，即 [5,7,23] 。

提示：

1 <= arr.length <= 1000
1 <= arr[i] <= 1000

这题没什么好说的了，直接模拟：

class Solution {
public:
    bool threeConsecutiveOdds(vector<int>& arr) {
        int n=arr.size();
        if(n<3) return false;
        for(int i=0;i<n-2;i++){
            if(arr[i]%2==1&&arr[i+1]%2==1&&arr[i+2]%2==1) return true;
        }
        return false;
    }
};

使数组中所有元素相等的最小操作数

存在一个长度为 n 的数组 arr ，其中 arr[i] = (2 * i) + 1 （ 0 <= i < n ）。

一次操作中，你可以选出两个下标，记作 x 和 y （ 0 <= x, y < n ）并使 arr[x] 减去 1 、arr[y] 加上 1 （即 arr[x] -=1 且 arr[y] += 1 ）。最终的目标是使数组中的所有元素都 相等 。题目测试用例将会 保证 ：在执行若干步操作后，数组中的所有元素最终可以全部相等。

给你一个整数 n，即数组的长度。请你返回使数组 arr 中所有元素相等所需的 最小操作数 。

示例1:

输入：n = 3
输出：2
解释：arr = [1, 3, 5]
第一次操作选出 x = 2 和 y = 0，使数组变为 [2, 3, 4]
第二次操作继续选出 x = 2 和 y = 0，数组将会变成 [3, 3, 3]

示例2:

输入：n = 6
输出：9

提示：

1 <= n <= 10^4

题目看起来不简单，看了一遍之后简单的我甚至以为自己理解错了。。其实肯定可以直接给出公式，周赛的时候就直接模拟了：

class Solution {
public:
    int minOperations(int n) {
        int res=0;
        int target=n;
        for(int i=1;i<target;i+=2){
            res+=target-i;
        }
        return res;
    }
};

两球间的磁力

在代号为 C-137 的地球上，Rick 发现如果他将两个球放在他新发明的篮子里，它们之间会形成特殊形式的磁力。Rick 有 n 个空的篮子，第 i 个篮子的位置在 position[i] ，Morty 想把 m 个球放到这些篮子里，使得任意两球间 最小磁力 最大。

已知两个球如果分别位于 x 和 y ，那么它们之间的磁力为 |x - y| 。

给你一个整数数组 position 和一个整数 m ，请你返回最大化的最小磁力。

示例1:

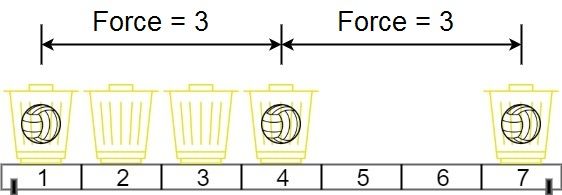
输入：position = [1,2,3,4,7], m = 3
输出：3
解释：将 3 个球分别放入位于 1，4 和 7 的三个篮子，两球间的磁力分别为 [3, 3, 6]。最小磁力为 3 。我们没办法让最小磁力大于 3 。

示例2:

输入：position = [5,4,3,2,1,1000000000], m = 2
输出：999999999
解释：我们使用位于 1 和 1000000000 的篮子时最小磁力最大。

提示：

• n == position.length
• 2 <= n <= 10^5
• 1 <= position[i] <= 10^9
• 所有 position 中的整数 互不相同 。
• 2 <= m <= position.length

题目说的花里胡哨，一看反正就是二分贪心的题，二分最小距离的最大值，f函数贪心检测该距离能否满足。

class Solution {
public:
    int f(vector<int>& position,int m,int mid){
        int tmp=1,last=0;
        for(int i=1;i<position.size();i++){
            if(position[i]-position[last]>=mid){
                tmp++;
                last=i;
            }
        }
        return tmp>=m;
    }
    int maxDistance(vector<int>& position, int m) {
        sort(position.begin(),position.end());
        int l=1,r=position.back()-position[0];
        while(l<r){
            int mid=(l+r+1)>>1;
            if(f(position,m,mid)) l=mid;
            else r=mid-1;
        }
        return l;
    }
};

吃掉N个橘子的最小天数

厨房里总共有 n 个橘子，你决定每一天选择如下方式之一吃这些橘子：

• 吃掉一个橘子。
• 如果剩余橘子数 n 能被 2 整除，那么你可以吃掉 n/2 个橘子。
• 如果剩余橘子数 n 能被 3 整除，那么你可以吃掉 2*(n/3) 个橘子。

每天你只能从以上 3 种方案中选择一种方案。请你返回吃掉所有 n 个橘子的最少天数。

示例1:

输入：n = 10
输出：4
解释：你总共有 10 个橘子。
第 1 天：吃 1 个橘子，剩余橘子数 10 - 1 = 9。
第 2 天：吃 6 个橘子，剩余橘子数 9 - 2*(9/3) = 9 - 6 = 3。（9 可以被 3 整除）
第 3 天：吃 2 个橘子，剩余橘子数 3 - 2*(3/3) = 3 - 2 = 1。
第 4 天：吃掉最后 1 个橘子，剩余橘子数 1 - 1 = 0。
你需要至少 4 天吃掉 10 个橘子。

示例2:

输入：n = 6
输出：3
解释：你总共有 6 个橘子。
第 1 天：吃 3 个橘子，剩余橘子数 6 - 6/2 = 6 - 3 = 3。（6 可以被 2 整除）
第 2 天：吃 2 个橘子，剩余橘子数 3 - 2*(3/3) = 3 - 2 = 1。（3 可以被 3 整除）
第 3 天：吃掉剩余 1 个橘子，剩余橘子数 1 - 1 = 0。
你至少需要 3 天吃掉 6 个橘子。

示例3:

输入：n = 1
输出：1

示例4:

输入：n = 56
输出：6

提示：

1 <= n <= 2*10^9

如果n的范围比较小的话是一道挺简单的题，但难就难在n的范围很大，所以逐个dp肯定是不行了。n的范围这么大，估计是可以贪心的，或者就想想如何优化自己的dp。竞赛的时候失误了没想到直接贪心，就在dp的基础上优化了一下：先对小于100000的情况dp求出结果，对于比较大的n，直接搜索，搜索到小于100000的时候就可以得到刚刚的结果，不用继续搜下去了。

• 之前的dp没什么好说的，从小到大遍历
• 搜索的时候加入了深度n，因为每次搜索都要减1会很慢，这里大概试了一下，当n在上界的时候也就二三十次的样子，所以设了个depth，超过20还没达到100000就直接剪枝了
• 不得不说方法不是很好，但也能在没思路的时候给一点思路，也一遍过了

class Solution {
public:
    int f(int dp[],int n,int depth){
        if(n<100000) return dp[n];
        if(depth>20) return INT_MAX-100;
        int res=1000;
        if(n%3==0) res=min(res,f(dp,n/3,depth+1)+1);
        if(n%2==0) res=min(res,f(dp,n/2,depth+1)+1);
        res=min(res,f(dp,n-1,depth+1)+1);
        return res;
    }
    int minDays(int n) {
        if(n==1) return 1;
        if(n==2) return 2;
        if(n==3) return 2;
        int dp[100000];
        dp[1]=1;
        dp[2]=2;
        dp[3]=2;
        for(int i=4;i<min(100000,n+1);i++){
            dp[i]=dp[i-1]+1;
            if(i%2==0) dp[i]=min(dp[i],dp[i/2]+1);
            if(i%3==0) dp[i]=min(dp[i],dp[i/3]+1);
        }
        if(n<100000) return dp[n];
        int res=f(dp,n,1);
        return res;
    }
};

当然最好的解法就是贪心，能被2整除的时候我们肯定要让他除，3也同理，如果不整除我们肯定是先减1，直到能够被整除再整除。具体减几次，或者说被2除还是3除，就要min比较一下。同样用map存储一下，优化时间。

class Solution {
public:
    map<int, int> dp;
    int minDays(int n) {
        if(n == 0) return 0;
        if(n == 1) return 1;
        if(dp.count(n)) return dp[n];
        int res = min(minDays(n / 2) + n % 2 + 1, minDays(n / 3) + n % 3 + 1);
        dp[n] = res;
        return res;
    }