贝叶斯网络框架

前言：

文章主要的目的是介绍eBay所使用的一个贝叶斯网络的框架，博主通过阅读相关论文和源代码以及代码测试，慢慢熟悉了该框架的使用方法及主要思想。

本文将尽量的阐述清楚贝叶斯网络的解决过程，如果你还不知道贝叶斯网络是解决哪一类问题的，请查看：贝叶斯网络笔记。

如果你能通过阅读论文熟悉贝叶斯网络，请尽量阅读论文，因为论文里一般都有详细的解释和公式化的证明过程。而本文的重点并不在于公式证明。（贝叶斯网络论文可以自行Google）

在阐述联合树算法的过程中，尽量去理解每段话的含义，如果实在理解不了的话，后面会给出一个案例，可以去结合案例来理解联合树算法的过程。

简介：

Bayesian-belief-networks 允许你用纯Python创建贝叶斯信念网络和其他图模型，目前支持四种不同的推理方法。

支持的图模型：
- 离散变量的贝叶斯信念网络
- 有着高斯分布的连续变量的高斯贝叶斯网络

推理引擎：
- 消息传递和联合树算法（Junction Tree Algorithm）
- 和积算法（The Sum Product Algorithm）
- MCMC采样的近似推理
- 高斯贝叶斯网络中得Exact Propagation

项目开源地址：
https://github.com/eBay/bayesian-belief-networks

框架解读

核心算法

联合树算法（Junction Tree Algorithm）：
其主要步骤包括：构建联合树 + 在联合树上进行消息传递。

如何构建联合树：

1. 对于给定的贝叶斯网络进行道德化，也就是将有向图转换为无向图，
   将每个有共同子节点的父节点连接起来，把所有的有向边改为无向边。

2. 将道德图三角化。原道德图记为G，复制得到的图记为g。
   每次选择图g的点观测顺序，选择规则为：val = （节点V的所有邻居节点 两两不是相邻节点的对数），优先选择val值小的。
   按照上述规则选好点V后，将节点V的所有邻居节点，两两不是相邻节点连边，图G中也连上边.
   cluster = [v] + v.neighbours
   在cliques中添加cluster，如果cluster不是cliques任何一个元素的子集。
   在g图中消去点V 以及所有与该点V相连的边。
   重复上述步骤，直到g图中不存在节点。
   如此图G便是三角化后的图。（添加了最少的边）
   同时得到了三角化图中各个团，即cliques(用于后面联合树的构建)。

3. 构建联合树。首先得到了三角化后的所有团节点Cliques,算法目的在于：将N个节点用N-1条边连接成一棵树，并且使得树最优，类似于克鲁斯卡尔算法（也就是一种最小生成树算法）。
   团节点之间两两组合取交集得到分离点Septor = intersection（Ci，Cj）
   选择最佳的分离点的标准为：

   1. 最大的mass = len(Septor)，即分离点里变量的数量。
   2. cost越小，cost = weight(Ci) + weight(Cj)

如何在联合树上进行消息传递：
（这里看着可能会比较懵，所以可以先看看后面的实例，再回头查看消息传递的过程）

下面就是在这颗树上进行若干次消息传递，从而完成数值的更新过程：
对于每个evidence variable，把它放到包括这个变量的表里，然后把所有不满足这个evidence的entry全设为0。

接着做一个自底向上的迭代，对于每个叶子节点，给它的父节点发送一个信息，即相关的表，父节点得到信息后就将其跟自己的表相乘，依次往上迭代，直到根节点。之后再做一个自顶向下的迭代，类似的，父节点向子节点发送信息，子节点得到信息后将其与自己的表相乘，依次往下迭代，直到所有叶子节点收到信息。

两个联合树节点之间的消息传播为：sender -> reciever
1、首先找到这两个节点的SepsetNode：intersecrtion(sender, reciever)
2、进行Projection步骤
3、进行Absorbtion步骤

框架结构：

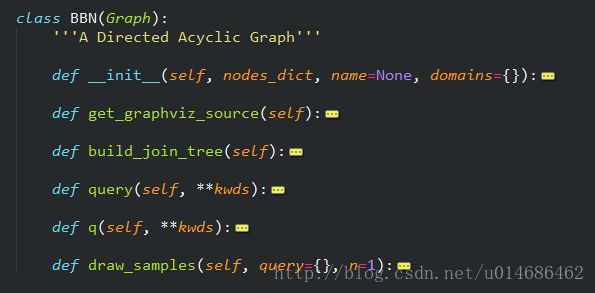
BBN为核心类，其q()方法用于接收参数得到网络中其他各个变量的边缘概率.

框架使用

首先按照项目的README文档说明 安装好相关模块。

接下来会结合一个实例来梳理整个贝叶斯网络的解决过程

测试文件：

from bayesian.bbn import *
def fP(P):
    '''Pollution'''
    if P == 'high':
        return 0.1
    elif P == 'low':
        return 0.9

def fS(S):
    '''Smoker'''
    if S is True:
        return 0.3
    elif S is False:
        return 0.7

def fC(P, S, C):
    '''Cancer'''
    table = dict()
    table['ttt'] = 0.05
    table['ttf'] = 0.95
    table['tft'] = 0.02
    table['tff'] = 0.98
    table['ftt'] = 0.03
    table['ftf'] = 0.97
    table['fft'] = 0.001
    table['fff'] = 0.999
    key = ''
    key = key + 't' if P == 'high' else key + 'f'
    key = key + 't' if S else key + 'f'
    key = key + 't' if C else key + 'f'
    return table[key]

def fX(C, X):
    '''X-ray'''
    table = dict()
    table['tt'] = 0.9
    table['tf'] = 0.1
    table['ft'] = 0.2
    table['ff'] = 0.8
    key = ''
    key = key + 't' if C else key + 'f'
    key = key + 't' if X else key + 'f'
    return table[key]

def fD(C, D):
    '''Dyspnoeia'''
    table = dict()
    table['tt'] = 0.65
    table['tf'] = 0.35
    table['ft'] = 0.3
    table['ff'] = 0.7
    key = ''
    key = key + 't' if C else key + 'f'
    key = key + 't' if D else key + 'f'
    return table[key]

def BBNSolver():
    g = build_bbn(
        fP, fS, fC, fX, fD,
        domains={
            'P': ['low', 'high']})
    return g

if __name__ == '__main__':
    g = BBNSolver()
    # print bbn Graph
    print g.get_graphviz_source()
    # print junction tree
    jt = g.build_join_tree()
    print jt.get_graphviz_source()
    g.q()
    # g.q(P='high')
    # g.q(D=True)
    # g.q(S=True)
    # g.q(C=True, S=True)
    # g.q(D=True, S=True)

测试文件用函数的形式给出了贝叶斯网络的结构，根据给定的函数可以看出该贝叶斯网络有5个节点，分别为：P，S，X，C，D。同时每个节点的概率分布表也由函数给出，例如函数fC(P, S, C)，说明了C变量会由P和S条件决定，所以可以知道该贝叶斯网络结构如下：

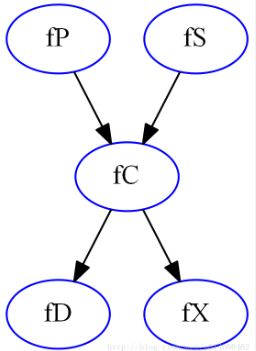
道德化：

对应函数：make_moralized_copy(gu, dag)
测试文件中的g变量就是class BBN，也就是本框架中的核心类，g = build_bbn(fP, fS, fC, fX, fD, domains={'P': ['low', 'high']}).
道德化过程为构建联合树的第一步，在函数build_join_tree(dag, clique_priority_func=priority_func)中被调用.
根据之前的叙述，可以得到道德化之后的图如下：

三角化：

对应函数：triangulate(gm, priority_func=priority_func)
三角化主要的目的是通过添加边的形式来消去图中超过三个点的简单环，同时得到团节点。
所以按照之前的三角化过程叙述步骤模拟进行，可以得出三角化后的团节点为：PSC，XC，CD

构建联合树：

该步骤的目的就是把三角化得到的团节点连接成一棵树，同时边的权值加权值最小，也就是得到一颗最小生成树。（请参考克鲁斯卡尔算法）
按照之前的构建联合树步骤模拟，得到最终的联合树为：

其中椭圆点表示团节点Clique，方块点表示分离节点Sepset。

在联合树上进行消息传递：

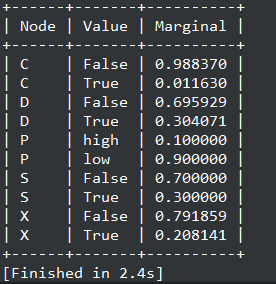
这一过程包括两次消息传递，用于得到每个节点的边缘概率，也就是函数g.q()执行后的结果。

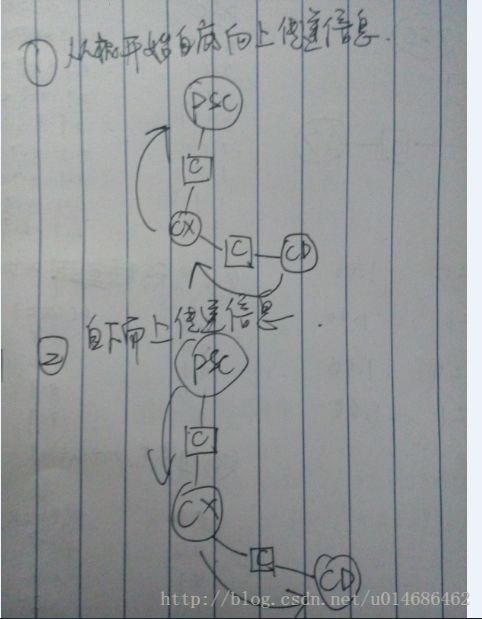
具体的消息传递处理过程为（主要是每个节点概率表的变化情况）：

初始化联合树上每个节点的概率表：

概率数据请参考测试文件

在联合树上进行消息传递：

消息传递完成后，可以得到联合树上每个节点的概率分布情况，进而可以求出每个变量的边缘分布。

得到变量边缘分布：

More：

如果要询问条件概率，例如：g.q(P='high')。就相当于联合树上多了一个evidence，那么在初始化的时候，就需要把团节点里面涉及到P='low'的概率赋值为0。但是消息传递过程相同。
如下是g.q(P='high')询问的结果：

参考资料：

• 贝叶斯网络理论基础
• 联合树论文_EN
• 联合树构建相关论文_CH

最后：

文章中如有错误，敬请指正，谢谢！
未经作者允许，禁止转载！