时间序列之间的相关性检测
为了检测时间序列的相关性,我们经常使用自相关,互相关或归一化互相关。
互相关(Cross-Correlation)
互相关是两个不同时间序列的比较,以检测具有相同最大值和最小值的指标之间是否存在相关性。例如:“两个音频信号同相吗?”
为了检测两个信号之间的相关程度,我们使用互相关。 只需将两个时间序列相乘和相加即可计算得出。
在以下示例中,序列A和B是互相关的,但序列C都不与此相关。
a = [1, 2, -2, 4, 2, 3, 1, 0]
b = [2, 3, -2, 3, 2, 4, 1, -1]
c = [-2, 0, 4, 0, 1, 1, 0, -2]
pyplot.figure()
pyplot.title("Series")
pyplot.plot(range(len(a)), a, color="#f44e2e", label="a")
pyplot.plot(range(len(b)), b, color="#27ccc0", label="b")
pyplot.plot(range(len(c)), c, color="#273ecc", label="c")
pyplot.ylabel("value")
pyplot.xlabel("index")
pyplot.show()
c r o s s _ c o r r ( x , y ) = ∑ i = 0 n − 1 x i ∗ y i cross\_corr(x, y) = \sum_{i=0}^{n-1} x_i*y_i cross_corr(x,y)=i=0∑n−1xi∗yi
使用上面的互相关公式,我们可以计算序列之间的相关度。
import numpy as np
def cross_corr(set1, set2):
return np.sum(set1 * set2)
a = np.array([1, 2, -2, 4, 2, 3, 1, 0])
b = np.array([2, 3, -2, 3, 2, 4, 1, -1])
c = np.array([-2, 0, 4, 0, 1, 1, 0, -2])
print(f"Cross Correlation a,b: {cross_corr(a, b)}")
print(f"Cross Correlation a,c: {cross_corr(a, c)}")
print(f"Cross Correlation b,c: {cross_corr(b, c)}")
OUTPUT:
Cross Correlation a,b: 41
Cross Correlation a,c: -5
Cross Correlation b,c: -4
序列a和b互相关性较大,值为41。序列a和c,a和b相关性较小,值分别为:-5,-4.
标准化的互相关(Normalized Cross-Correlation)
标准化的互相关也是用于两个时间序列的比较,但是使用了不同的评分结果。除了简单的互相关,它还可以比较具有不同值范围的指标。例如:“商店中的顾客数量与每天的销售数量之间是否存在相关性?”
使用互相关值评价相关性存在三个问题:
- 互相关的评分值难以理解。
- 两个序列必须具有相同的幅度。如如果一个序列值缩小了一半,那么他的相关性会减少。 c r o s s _ c o r r ( a , a / 2 ) = 19.5 cross\_corr(a,a/2)=19.5 cross_corr(a,a/2)=19.5
- 无法解决序列值为0的问题,根据互相关公式,由于 0 ∗ 0 = 0 0*0=0 0∗0=0和 0 ∗ 200 = 0 0*200=0 0∗200=0,因此无法解决0值。
为了解决这些问题,使用标准化的互相关:
n o r m _ c o r r ( x , y ) = ∑ n = 0 n − 1 x i ∗ y i ∑ n = 0 n − 1 x i 2 ∗ ∑ n = 0 n − 1 y i 2 norm\_corr(x,y)=\dfrac{\sum_{n=0}^{n-1} x_i*y_i}{\sqrt{\sum_{n=0}^{n-1} x_i^2 * \sum_{n=0}^{n-1} y_i^2}} norm_corr(x,y)=∑n=0n−1xi2∗∑n=0n−1yi2∑n=0n−1xi∗yi
计算上边a,b,c序列的标准化的相关性如下:
import numpy as np
def norm_cross_corr(set1, set2):
# python中求Normalized Cross Correlation的函数是: statsmodels.tsa.stattools.ccf
return np.sum(set1 * set2) / (np.linalg.norm(set1) * np.linalg.norm(set2))
a = np.array([1, 2, -2, 4, 2, 3, 1, 0])
b = np.array([2, 3, -2, 3, 2, 4, 1, -1])
c = np.array([-2, 0, 4, 0, 1, 1, 0, -2])
print(f"Normalized Cross Correlation a,b: {norm_cross_corr(a, b)}")
print(f"Normalized Cross Correlation a,c: {norm_cross_corr(a, c)}")
print(f"Normalized Cross Correlation b,c: {norm_cross_corr(b, c)}")
OUTPUT:
Normalized Cross Correlation a,b: 0.9476128352180998
Normalized Cross Correlation a,c: -0.15701857325533194
Normalized Cross Correlation b,c: -0.11322770341445959
标准化的互相关值很容易理解:
- 值越高,相关性越高。
- 当两个信号完全相同时,最大值为1: n o r m _ c r o s s _ c o r r ( a , a ) = 1 norm\_cross\_corr(a,a)=1 norm_cross_corr(a,a)=1
- 当两个信号完全相反时,最小值为-1: n o r m _ c r o s s _ c o r r ( a , − a ) = − 1 norm\_cross\_corr(a,-a)=-1 norm_cross_corr(a,−a)=−1
标准化的互相关可以检测两个幅度不同的信号的相关性,如: n o r m _ c r o s s _ c o r r ( a , a / 2 ) = 1 norm\_cross\_corr(a,a/2)=1 norm_cross_corr(a,a/2)=1。信号A和具有一半振幅的同一信号之间具有最高的相关性!
自相关(Auto-Correlation)
自相关是时间序列在不同时间与其自身的比较。例如,其目的是检测重复模式或季节性。例如:“服务器网站上是否有每周的季节性?”“本周的数据与前一周的数据高度相关吗?”
自相关的用途非常广泛,其中之一就是检测由于季节性导致的可重复的模式。
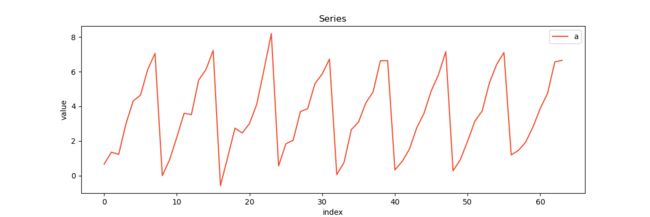
下图展示了具有季节性为8的序列:
import numpy as np
np.random.seed(10)
a = np.tile(np.array(range(8)), 8) + np.random.normal(loc=0.0, scale=0.5, size=64)
pyplot.figure(figsize=(12, 4))
pyplot.title("Series")
pyplot.plot(range(len(a)), a, color="#f44e2e", label="a")
pyplot.ylabel("value")
pyplot.xlabel("index")
pyplot.legend(loc="upper right")
pyplot.show()
图像由如上代码生成,他是1~8的可重复序列,并且夹杂了一些随机噪声。
接下来计算时间偏移为4和时间偏移为8时信号与自身之间的自相关。

import numpy as np
np.random.seed(10)
a = np.tile(np.array(range(8)), 8) + np.random.normal(loc=0.0, scale=0.5, size=64)
ar4 = a[:len(a) - 4]
ar4_shift = a[4:]
print(f"Auto Correlation with shift 4: {cross_correlation(ar4, ar4_shift)}")
pyplot.figure(figsize=(12, 4))
pyplot.title("Series")
pyplot.plot(range(len(ar4)), ar4, color="blue", label="ar4")
pyplot.plot(range(len(ar4_shift)), ar4_shift, color="green", label="ar4_shift")
pyplot.ylabel("value")
pyplot.xlabel("index")
pyplot.legend(loc="upper right")
pyplot.show()
OUTPUT:
Auto Correlation with shift 4: 623.797612892277
import numpy as np
np.random.seed(10)
a = np.tile(np.array(range(8)), 8) + np.random.normal(loc=0.0, scale=0.5, size=64)
ar8 = a[:len(a) - 8]
ar8_shift = a[8:]
print(f"Auto Correlation with shift 4: {cross_correlation(ar8, ar8_shift)}")
pyplot.figure(figsize=(12, 4))
pyplot.title("Series")
pyplot.plot(range(len(ar4)), ar4, color="blue", label="ar4")
pyplot.plot(range(len(ar4_shift)), ar4_shift, color="green", label="ar4_shift")
pyplot.ylabel("value")
pyplot.xlabel("index")
pyplot.legend(loc="upper right")
pyplot.show()
OUTPUT:
Auto Correlation with shift 8: 996.8417240253186
上图清楚地显示了时间偏移8处的高自相关,而时间偏移4处没有。计算出的自相关值可以看到shift为8时的自相关值大于shift为4时的值。所以相比于4,我们觉得季节性更可能为8。
标准化的自相关(Normalized Auto-Correlation)
如前所述,用标准化的互相关可以更好地表达两个序列的相关性
print(f"Auto Correlation with shift 4: {norm_cross_correlation(ar4, ar4_shift)}")
print(f"Auto Correlation with shift 8: {norm_cross_correlation(ar8, ar8_shift)}")
OUTPUT:
Auto Correlation with shift 4: 0.5779124931215941
Auto Correlation with shift 8: 0.9874907451139486
相关性与时移(Correlation with Time Shift)
标准化的互相关与时移(Normalized Cross-Correlation with Time Shift)
时移可以应用于所有上述算法。想法是将指标与具有不同“时间偏移”的另一个指标进行比较。将时间偏移应用于归一化互相关函数将导致“具有X的时间偏移的归一化互相关”。这可以用来回答以下问题:“当许多顾客进我的商店时,我的销售额在20分钟后会增加吗?”
为了处理时移,我们将原始信号与由x元素向右或向左移动的另一个信号关联。就像我们为自相关所做的一样。
为了检测两个指标是否与时移相关,我们需要计算所有可能的时移。
from statsmodels.tsa.stattools import ccf
a = np.array([0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4])
b = np.array([1, 2, 3, 3, 0, 1, 2, 3, 4, 0, 1, 1, 4, 4, 0, 1, 2, 3, 4, 0])
res_ary = ccf(a, b, unbiased=False) # 计算各种time shift下的互相关值
print(res_ary)
pyplot.bar(range(len(res_ary)), res_ary, fc="blue")
pyplot.show()
OUTPUT:
[-3.29180823e-17 8.67261700e-01 1.27247799e-01 -4.65751654e-01
-3.92862138e-01 -1.09726941e-17 6.20178595e-01 1.27247799e-01
-2.92793480e-01 -2.94028896e-01 -2.47083106e-02 3.48387179e-01
1.02539489e-01 -1.19835306e-01 -1.70487343e-01 -2.47083106e-02
1.01304073e-01 5.31228677e-02 -2.10020640e-02 -4.69457901e-02]
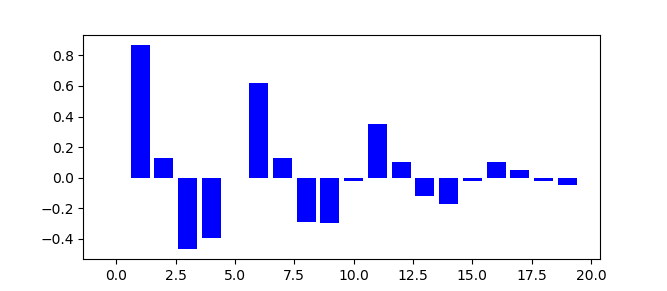
从上图以及数据可以看出,当time shift为1时,序列a和b高度相关。
标准化的自相关与时移(Normalized Auto-Correlation with Time Shift)
from statsmodels.tsa.stattools import acf
np.random.seed(5)
a = np.tile(np.array(range(8)), 8) + np.random.normal(loc=0.0, scale=0.5, size=64)
res_ary = acf(a, nlags=30, fft=False)
print(res_ary)
pyplot.bar(range(len(res_ary)), res_ary, fc="blue")
pyplot.show()
OUTPUT:
[ 1. 0.33436187 -0.06325233 -0.39112367 -0.46168766 -0.43537856
-0.15175395 0.24403119 0.86075234 0.31051923 -0.03270547 -0.32083613
-0.40031665 -0.38383002 -0.14645852 0.20649692 0.72864895 0.2693097
-0.01707009 -0.2658133 -0.3339456 -0.32771517 -0.1214095 0.17008013
0.60740024 0.22492556 -0.01633838 -0.21157885 -0.27896827 -0.27765971
-0.10762048]
原始序列是有8的季节性,自相关检测也看到了在8的整数倍的偏移处得到了较高的自相关值。
将相关指标聚类(Cluster Correlated Metrics Together)
我们可以用Normalized Cross Correlation,根据相似度将相关性较大的metric聚类。
使用数据集:graphs45.csv
import numpy as np
import pandas as pd
def get_correlation_table(metric_df):
metric_cnt = metric_df.shape[1]
correlation_table = np.zeros((metric_cnt, metric_cnt))
for i in range(metric_cnt):
metric_1 = metric_df.iloc[:, i]
for j in range(metric_cnt):
if i == j:
continue
else:
metric_2 = metric_df.iloc[:, j]
cc_ary = ccf(metric_1, metric_2, unbiased=False)
correlation_table[i, j] = cc_ary[0]
return correlation_table
def find_related_metric(correlation_table, orig, high_corr):
metric_corr_table = correlation_table[orig]
corr_metric_lst = []
for i in range(len(metric_corr_table)):
if metric_corr_table[i] > high_corr:
corr_metric_lst.append(i)
return corr_metric_lst
if __mian__:
metric_df = pd.read_csv("./graphs45.csv")
correlation_table_ary = get_correlation_table(metric_df)
orig = 3
high_corr = 0.9
corr_metric_lst = find_related_metric(correlation_table_ary, orig, high_corr)
corr_metric_lst.append(orig)
print(corr_metric_lst)
pyplot.figure()
pyplot.title("Series")
for idx in corr_metric_lst:
metric = metric_df.iloc[:, idx]
pyplot.plot(range(len(metric)), metric, label=f"graph_{idx + 1}")
pyplot.ylabel("value")
pyplot.xlabel("index")
pyplot.legend(loc="upper right")
pyplot.show()
get_correlation_table()计算了所有metric之间的标准化的互相关值,结果存在correlation_table中,correlation_table[i,j]代表第i个metric和第j个metric之间的相关值。
然后find_related_metric()根据相关值表找出和graph_4相关值大于0.9的序列,最后找出的相关序列画图如下:
参考
- Understanding Cross-Correlation, Auto-Correlation, Normalization and Time Shift
- Detecting Correlation Among Multiple Time Series