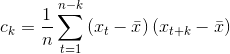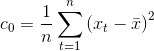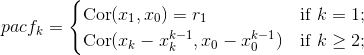数据序列相关性-ACF，PACF和CCF（更新中...）
引言
最近写论文关于预测的特征选择遇到一些问题，想把自己查询学习到的东西整理记录一下，理一理头绪，希望能加深自己对这些东西的理解。首先介绍引入几个概念：自相关函数（autocorrelation function，ACF）、偏自相关函数（partial autocorrelation，PACF）和互相关函数（cross-correlation function，CCF）。接下来介绍每个指标的计算方法和用途：
1. ACF
顾名思义，自相关函数是针对单个时间序列的，对于时间序列
,滞后k阶的自协方差函数（autocovariance function，ACVF）为[1]:
，
即
ACF被定义为：
我理解的也等同于序列与
的pearson相关系数。置信区间一般使用下式进行计算[2]：
下面是一个简单的计算程序，是对statsmodels模块的源代码进行简化得到的[3]。
from scipy.stats import norm
import numpy as np
def acf(x,nlags=40, alpha=None):
# Calculate the autocorrelation function.
nobs = len(x)
avf = acovf(x,nlag = nlags)
acf = avf[:nlags + 1] / avf[0]
if alpha is not None:
varacf = np.ones(nlags + 1) / nobs
varacf[0] = 0
varacf[1] = 1. / nobs
varacf[2:] *= 1 + 2 * np.cumsum(acf[1:-1]**2)
interval = norm.ppf(1 - alpha / 2.) * np.sqrt(varacf)
confint = np.array(lzip(acf - interval, acf + interval))
return acf, confint
else:
return acf
def acovf(x,nlag=None):
# Estimate autocovariances.
xo = x - x.mean()
n = len(x)
lag_len = nlag
if nlag is None:
lag_len = n - 1
elif nlag > n - 1:
raise ValueError('nlag must be smaller than nobs - 1')
acov = np.empty(lag_len + 1)
acov[0] = xo.dot(xo)
for i in range(lag_len):
acov[i + 1] = xo[i + 1:].dot(xo[:-(i + 1)])
return acov
理解了原理可以这样。
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import acf
from statsmodels.graphics.tsaplots import plot_acf
x = pd.read_excel('resample.xls',index_col=0,date_parse=True)
acf_x, interval = acf(x=x,nlags=10,alpha=0.05)
print('ACF:\n',acf_x)
print('ACF95%置信区间下界:\n',interval[:,0]-acf_x)
print('ACF95%置信区间上界:\n',interval[:,1]-acf_x)
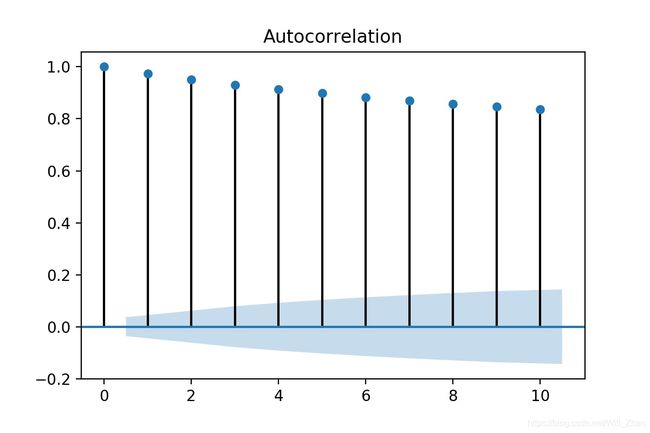
plot_acf(x=x,lags=10,alpha=0.05)
plt.show()输出结果：
ACF: [1. 0.97339745 0.95013662 0.93091665 0.91399405 0.89897186 0.88282934 0.86933546 0.85708885 0.84621534 0.83720026] ACF95%置信区间下界: [ 0. -0.03625835 -0.06169254 -0.07861061 -0.09196861 -0.10322176 -0.11304703 -0.12177398 -0.12967655 -0.13692158 -0.14363264] ACF95%置信区间上界: [0. 0.03625835 0.06169254 0.07861061 0.09196861 0.10322176 0.11304703 0.12177398 0.12967655 0.13692158 0.14363264]
[1] https://nwfsc-timeseries.github.io/atsa-labs/sec-tslab-correlation-within-and-among-time-series.html : Book, Applied Time Series Analysis for Fisheries and Environmental Sciences
[2] https://www.statsmodels.org/stable/_modules/statsmodels/tsa/stattools.html#acf : Python modular, statsmodels
[3] https://www.itl.nist.gov/div898/handbook/eda/section3/autocopl.htm : Engineering statistics handbook
2. PACF
偏自相关函数也是针对单个时间序列的，关于其和ACF的区别，[4] 进行了一般性的易于理解的解释，我在这里根据自己的理解进行简要翻译一下。
偏自相关函数是序列与滞后k阶的序列
的线性相关性，移除
的线性依赖，计算公式为：
滞后1阶的pacf与滞后1阶的acf相等，不存在滞后0阶的pacf。
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import pacf
from statsmodels.graphics.tsaplots import plot_pacf
x = pd.read_excel('resample.xls',index_col=0,date_parse=True)
pacf_x, interval = pacf(x=x,nlags=10,alpha=0.05)
print('PACF:\n',pacf_x)
print('PACF95%置信区间下界:\n',interval[:,0]-pacf_x)
print('PACF95%置信区间上界:\n',interval[:,1]-pacf_x)
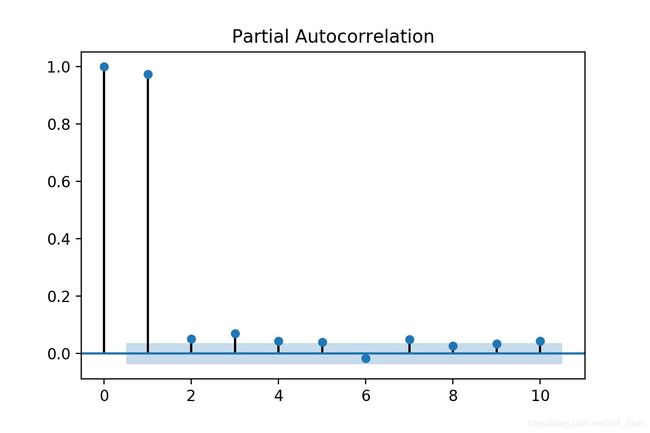
plot_pacf(x=x,lags=10,alpha=0.05)
plt.savefig('acf1.jpg',dpi=200)
plt.show()PACF: [ 1. 0.97373069 0.05083912 0.07012207 0.04486007 0.04104969 -0.01595041 0.0505279 0.02666616 0.03388021 0.04459499] PACF95%置信区间下界: [ 0. -0.03625835 -0.03625835 -0.03625835 -0.03625835 -0.03625835 -0.03625835 -0.03625835 -0.03625835 -0.03625835 -0.03625835] PACF95%置信区间上界: [0. 0.03625835 0.03625835 0.03625835 0.03625835 0.03625835 0.03625835 0.03625835 0.03625835 0.03625835 0.03625835]
3. CCF
交叉相关系数是针对两个时间序列的，对于时间序列和
，先计算互协方差函数：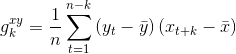
CCF的定义类似ACF：
其中，
分别为
的标准差。同时，应该注意的是
，
。其中，y是解释变量，x是预测因子。CCF的95%的置信区间计算公式定义为[1]:
其中n是用于计算互相关系数的样本数量。
import pandas as pd
from statsmodels.tsa.stattools import ccf
x = pd.read_excel('resample.xls',index_col=0,date_parse=True)
ccf_x = ccf(x=x.values.ravel(),y=x.values.ravel())
print('CCF:\n',ccf_x[:10])输出是： CCF: [1. 0.97373069 0.95078739 0.9318734 0.91524696 0.90051278 0.88464586 0.87142306 0.85944187 0.8488298 ]
附录：
1. 计算ccf，acf和pcf的置信区间的时候，和数据序列的长度有关系，长度取多少的时候比较合适？