R语言相关性分析
文章目录
- @[toc]
- Pearson相关系数(积差相关系数)
- 适用条件
- Spearman等级相关系数
- 适用条件
- Kendall's Tau相关系数
- 适用条件
- 偏相关
- 适用条件
- R语言实现
- Pearson、Spearman、Kendall
- 示例
- 偏相关
- 相关性显著性检验
- 相关性可视化
- 在这里插入图片描述
文章目录
- @[toc]
- Pearson相关系数(积差相关系数)
- 适用条件
- Spearman等级相关系数
- 适用条件
- Kendall's Tau相关系数
- 适用条件
- 偏相关
- 适用条件
- R语言实现
- Pearson、Spearman、Kendall
- 示例
- 偏相关
- 相关性显著性检验
- 相关性可视化
- 在这里插入图片描述
相关性分析就是通过定量指标描述变量之间的强弱、直接或间接的联系。
常见相关性指标
- Pearson相关系数(积差相关系数)
- Spearman等级相关系数
- Kendall’s Tau相关系数
- 偏相关
Pearson相关系数(积差相关系数)
Pearson相关系数是用于表示相关性大小的最常用指标,数值介于-1~1之间,越接近0相关性越低,越接近-1或1相关性越高。正负号表明相关方向,正号为正相关、负号为负相关。
适用条件
- 两个正态分布的连续变量
Spearman等级相关系数
又称为秩相关系数,利用两变量的秩次大小来进行分析,属于非参数统计方法。
适用条件
- 适用于不满足Pearson相关系数正态分布要求的连续变量。
- 也可以用于有序分类变量的之间的相关性测量。
Kendall’s Tau相关系数
Kendall’s Tau相关系数是一种非参数检验。
适用条件
- 适用于两个有序分类变量。
偏相关
当要进行相关性分析的两个变量其取值受到其他变量影响时,可以利用偏相关分析对其他变量进行控制,在控制其他变量基础之上进行这两个变量之间相关性分析。
适用条件
- 考虑第三方影响的两个变量之间的相关性分析。
R语言实现
Pearson、Spearman、Kendall
Pearson、Spearman、Kendall相关系数都可以通过cor函数实现,cov协方差函数参数同cor函数。
协方差是相关分析中一个重要概念,方差是协方差的一种特殊存在。样本协方差是离均差乘积在样本中的平均,可以近似反映变量x与变量y之间的联系强弱和方向。协方差可以引出相关分析概念。
协方差的大小与x、y的量纲有关。
函数格式基本为:
cor(x,use=,method=)
| 参数 | 描述 |
|---|---|
| x | 矩阵或数据框 |
| use | 指定缺失数据的处理方式。可选项:all.obs(假设不存在缺失数据)、everything(数据存在缺失值时,相关系数计算结果会显示missing)、complete.obs(行删除)、pairwise.complete.obs(成对删除) |
| method | 指定相关系数的类型。可选类型为pearson、spearman、kendall |
默认为use=‘everything’,method=‘pearson’
示例
- 数据集
state.x77:R语言自带美国50州1977年的人口、收入、文盲率、预期寿命、谋杀率和高中毕业率数据。
#选中state.x77数据集收入与高中毕业率变量
states <- state.x77[,c(2,6)]
#协方差
cov(states)
Income HS Grad
Income 377573.306 3076.76898
HS Grad 3076.769 65.23789
#相关性分析
cor(states)
Income HS Grad
Income 1.0000000 0.6199323
HS Grad 0.6199323 1.0000000
#spearman相关
cor(states,method = 'spearman')
Income HS Grad
Income 1.0000000 0.5104809
HS Grad 0.5104809 1.0000000
#结果显示,收入与高中毕业率有较高相关性
偏相关
使用ggm包pcor()函数计算偏相关系数。
函数调用格式为:
pcor(u,s)
其中,U为一个数值向量,前两个数值表示要计算相关系数的变量下标,其余变量为条件变量下标。S为变量的协方差矩阵。
#载入ggm包
library(ggm)
#生成数据集
states <- state.x77[,1:6]
#获取数据集各变量名称
colnames(states)
[1] "Population" "Income"
[3] "Illiteracy" "Life Exp"
[5] "Murder" "HS Grad"
#计算偏相关
pcor(c(1,5,2,3,6),cov(states))
[1] 0.3462724
#结果显示,在控制了收入、文盲率个高中毕业率影响时,人口和谋杀率之间的相关系数为0.346
相关性显著性检验
使用cor.test()函数对单个Pearson、Spearman、kendall相关系数进行检验。
函数格式为:
cor.test(x,y,alternative=’’,method=)
其中,x和y为要检验相关性的变量,alternative则用来指定进行双侧检验或单侧检验(‘two.side’、‘less’、‘greater’)。method用以指定要计算的相关类型(Pearson、Spearman、kendall)。
#检验预期寿命与谋杀率相关性。
cor.test(states[,3],states[,5])
Pearson's product-moment
correlation
data: states[, 3] and states[, 5]
t = 6.8479, df = 48, p-value =
1.258e-08
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.5279280 0.8207295
sample estimates:
cor
0.7029752
#结果显示,P大于0.05。即两者之间相关性微乎其微。
cor.test()每次只能检验一种相关关系。
psych包中corr.test()可以一次检验多种。
library(psysh)
corr.test(states,use = 'complete')
#结果太大,不再展示
相关性可视化
这里只展示最简单的相关性可视化方法。
详细内容见绘图文章板块
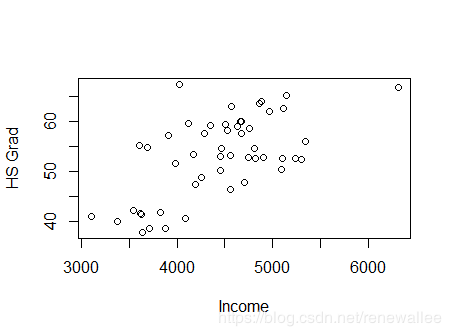
最简单两个连续变量相关性可视化用散点图表达。
使用plot()函数即可。
#选中变量收入与高中毕业率
states <- state.x77[,c(2,6)]
#绘图
plot(states)