深入理解协方差

1.协方差

1.1 均值、标准差、方差

均值：$\bar{X}=E(X)=\frac{1}{n}{\sum }_{i=1}^n{X}_i$

方差：$s^2=D(X)=\frac{1}{n-1}{\sum }_{i=1}^n(X_i-\bar{X}{)}^2$

标准差：$s=\sqrt{D(X)}=\sqrt{\frac{1}{n-1}{\sum }_{i=1}^n(X_i-\bar{X}{)}^2}$

均值描述样本集合的中间点，标准差描述样本集合的各个样本点到均值的距离之平均。

除以n-1而不是除以n，是因为这样能使我们以较小的样本集更好的逼近总体的标准差，即“无偏估计”。

1.2 协方差

标准差和方差一般是用来描述一维数据的，协方差是用来度量两个随机变量关系的统计量。

协方差：$cov(X,Y)=\frac{1}{n-1}{\sum }_{i=1}^n(X-\overline{X_i})(Y-\overline{Y_i})$

上式是求$(X-\overline{X_i})(Y-\overline{Y_i})$的均值，所以还可以写做：
$cov(X,Y)=E[(X-E(X))(Y-E(Y))]=E(XY)-E(X)E(Y)$

协方差的性质：

1. $cov(X,X)=var(X)$
2. $cov(X,Y)=cov(Y,X)$
3. $cov(X,Y)=cov(Y,X)$
4. $cov(AX+C,BY)=ABcov(X,Y)$
5. $cov(X+Y,Z)=cov(X,Z)+cov(Y,Z)$

2 协方差矩阵

2.1 协方差矩阵的定义

协方差是处理二维问题，那维数多了自然就需要计算多个协方差，用矩阵来组织这些数据，该矩阵叫做协方差矩阵。
给出协方差矩阵的定义：
设$X=(X_1,X_2,...,X_n)$为$n$维随机变量，称矩阵：

为$n$维随机变量，$X$的协方差矩阵(covariance matrix)，也记为$D(X)$，其中
$$c_{ij}=cov(X_i,X_j),i,j=1,2,...,n$$

因为$c_{ij}=c_{ji}$，所以协方差矩阵都是对称阵。

例如，二维随机变量$(X,Y)$的协方差矩阵为:

$$C=(c_{ij}{)}_{2\ast 2}=\left(\begin{array}{cc}{c}_{11}& c_{12}\\ c_{21}& c_{22}\end{array}\right)=\left(\begin{array}{cc}E[X-E(X){]}^2& E[(X-E(X))(Y-E(Y))]\\ E[(Y-E(Y))(X-E(X))]& E[Y-E(Y){]}^2\end{array}\right)$$

>> x=[[2,4,8,10],[3,5,1,7]]
>> np.cov(x)
array([[13.33333333,  2.66666667],
       [ 2.66666667,  6.66666667]])

三维随机变量$(X,Y,Z)$的协方差矩阵：

$$C=\left(\begin{array}{ccc}cov(X,X)& cov(X,Y)& cov(X,Z)\\ cov(Y,X)& cov(Y,Y)& cov(Y,Z)\\ cov(Z,X)& cov(Z,Y)& cov(Z,Z)\end{array}\right)$$

2.2 总结

理解协方差矩阵的关键就在于牢记它计算的是不同维度之间的协方差，而不是不同样本之间（但是，要求每个协方差项，则要使用各个样本来计算:$\frac{1}{n-1}{\sum }_{i=1}^n(x_i-{\mu }_x)(y_i-{\mu }_y)$），拿到一个样本矩阵，我们最先要明确的就是一行是一个样本还是一个维度，心中明确这个整个计算过程就会顺流而下。

3. 协方差和皮尔森相关系数

用协方差表示$X$和$Y$之间的关系时会受$X$与$Y$量纲的影响。所以再计算X与Y的协方差之前，先对X与Y进行标准化处理，即对于随机变量$(X,Y)$：

$$X^{\ast }=\frac{X-E(X)}{\sqrt{D(X)}},Y^{\ast }=\frac{Y-E(Y)}{\sqrt{D(Y)}}$$

由协方差的性质可得：

$$cov(X^{\ast },Y^{\ast })=cov(\frac{X-E(X)}{\sqrt{D(X)}},\frac{Y-E(Y)}{\sqrt{D(Y)}})=\frac{cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}$$

$cov(X^{\ast },Y^{\ast })$是无量纲的量，这样就消除了量纲对相关性的影响，其实$cov(X^{\ast },Y^{\ast })$就是相关系数，用${\rho }_{XY}$表示。

${\rho }_{XY}>0$表示两个变量正相关，且相关系数越大，正相关性越高；
${\rho }_{XY}<0$表示两个变量负相关，且相关系数越小，负相关性越高；
${\rho }_{XY}=0$表示两个变量不相关。

3. 协方差的意义

协方差为什么能表示两个随机变量的相关性，下面从两个方面解释：

3.1 从协方差公式

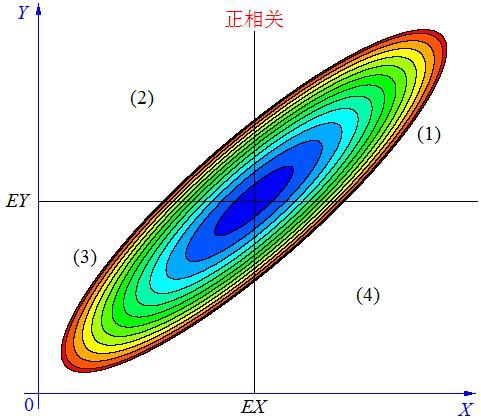
在概率论中，两个随机变量$X$与$Y$之间相互关系，大致有下列3种情况：

当$X$,$Y$的联合分布像上图那样时，我们可以看出，大致上有：$X$越大$Y$也越大，$X$越小$Y$也越小，这种情况，我们称为“正相关”。

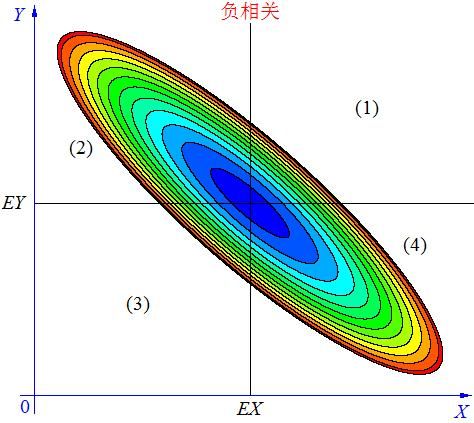
当$X$,$Y$的联合分布像上图那样时，我们可以看出，大致上有：$X$越大$Y$反而越小，$X$越小$Y$反而越大，这种情况，我们称为“负相关”。

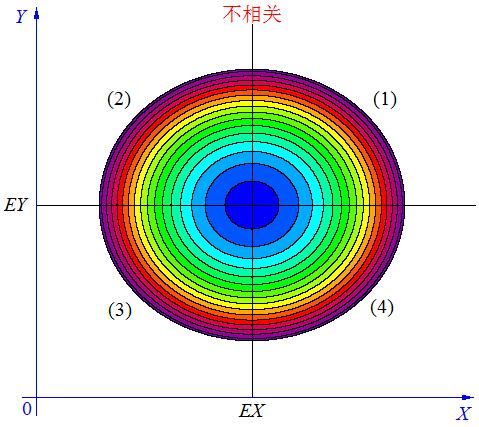
当$X$,$Y$的联合分布像上图那样时，我们可以看出：既不是$X$越大$Y$也越大，也不是$X$越大$Y$反而越小，这种情况我们称为“不相关”。

怎样将这3种相关情况，用一个简单的数字表达出来呢？

在图中的区域（1）中，有$X>EX，Y-EY>0$，所以$(X-EX)(Y-EY)>0$；
在图中的区域（2）中，有$X<EX，Y-EY>0$，所以$(X-EX)(Y-EY)<0$；
在图中的区域（3）中，有$X<EX，Y-EY<0$，所以$(X-EX)(Y-EY)>0$；
在图中的区域（4）中，有$X>EX，Y-EY<0$，所以$(X-EX)(Y-EY)<0$。

当$X$与$Y$正相关时，它们的分布大部分在区域（1）和（3）中，小部分在区域（2）和（4）中，所以平均来说，有$E(X-EX)(Y-EY)>0$。
当$X$与$Y$负相关时，它们的分布大部分在区域（2）和（4）中，小部分在区域（1）和（3）中，所以平均来说，有$(X-EX)(Y-EY)<0$。
当$X$与$Y$不相关时，它们在区域（1）和（3）中的分布，与在区域（2）和（4）中的分布几乎一样多，所以平均来说，有$(X-EX)(Y-EY)=0$。

所以，我们可以定义一个表示$X$,$Y$相互关系的数字特征，也就是协方差：$cov(X,Y)=E(X-EX)(Y-EY)$。

当$cov(X,Y)>0$时，表明$X$与$Y$正相关；
当$cov(X,Y)<0$时，表明$X$与$Y$负相关；
当$cov(X,Y)=0$时，表明$X$与$Y$不相关。

3.2 从向量的角度

对于两个随机变量$X=(x_1,x_2,...,x_n)$和$Y=(y_1,y_2,...,y_n)$，表示空间中的两个向量，讲两个向量做去均值处理得到$X^{\ast }=X-E(X)$,$Y^{\ast }=Y-Y(Y)$，对于空间中的两个向量，可以从向量的角度衡量两个向量的相关性：如果两个向量角度为90度，说明两个向量不相关（即变化趋势一点不同），如果两个向量角度为0度，说明两个向量极度相关，变化趋势一致，如果两个向量角度为180度，说明两个向量变化趋势相反。根据余弦公式：

$$cos(\theta )=\frac{X^{\ast }{Y}^{\ast }}{|X^{\ast }||Y^{\ast }|}=\frac{{\sum }_{i=1}^n(X_i-E(X))(Y_i-E(Y))}{\sqrt{{\sum }_{i=1}^n(X_i-E(X){)}^2}\sqrt{{\sum }_{i=1}^n(Y_i-E(Y){)}^2}}=\frac{cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}={\rho }_{XY}$$

参考

1. https://blog.csdn.net/goodshot/article/details/50961720
2. https://blog.csdn.net/GoodShot/article/details/79940438