#置换实验 Coin包
install.packages(c("coin"))
#lmPerm包
install.packages("lmPerm")
#独立两样本和K样本检验
library(coin)
score<-c(40,57,45,55,58,57,64,55,62,65)
treatment<-factor(c(rep("A",5),rep("B",5)))
mydata<-data.frame(treatment,score)
t.test(score~treatment,data=mydata,var.equal=TRUE)
Two Sample t-test
data: score by treatment
t = -2.345, df = 8, p-value = 0.04705
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-19.0405455 -0.1594545
sample estimates:
mean in group A mean in group B
51.0 60.6
#置换T检验
library(coin)
oneway_test(score~treatment,data=mydata,distribution="exact")
Exact Two-Sample Fisher-Pitman Permutation Test
data: score by treatment (A, B)
Z = -1.9147, p-value = 0.07143
alternative hypothesis: true mu is not equal to 0
结果显著:P<0.05
结果不显著:P>0.05
上面这两个测试中所得的P值相差比较大,并且样本容易比较小,所以置换T检验更有说服力,因此我们认为改组样本得到的结果不显著P>0.05
#Wilcox.test library(MASS) UScrime<-transform(UScrime,So=factor(So)) wilcox_test(Prob~So,data=UScrime,distribution="exact")
Exact Wilcoxon-Mann-Whitney Test
data: Prob by So (0, 1)
Z = -3.7493, p-value = 8.488e-05
alternative hypothesis: true mu is not equal to 0
wilcox.test(Prob~So,data=UScrime,distribution="exact")
Wilcoxon rank sum test
data: Prob by So
W = 81, p-value = 8.488e-05
alternative hypothesis: true location shift is not equal to 0
#chisq_Test library(coin) library(vcd) Arthritis<-transform(Arthritis,Improved=as.factor(as.numeric(Improved))) set.seed(1234) chisq_test(Treatment~Improved,data=Arthritis,distribution=approximate(B=9999))
Approximative Pearson Chi-Squared Test
data: Treatment by Improved (1, 2, 3)
chi-squared = 13.055, p-value = 0.0018
#spearman.test 数值变量间的独立性 states<-as.data.frame(state.x77) set.seed(1234) spearman_test(Illiteracy~Murder,data=states,distribution=approximate(B=9999))
Approximative Spearman Correlation Test
data: Illiteracy by Murder
Z = 4.7065, p-value < 2.2e-16
alternative hypothesis: true rho is not equal to 0
#两样本和K样本相关性检验 library(coin) library(MASS) wilcoxsign_test(U1~U2,data=UScrime,distribution="exact")
Exact Wilcoxon-Pratt Signed-Rank Test
data: y by x (pos, neg)
stratified by block
Z = 5.9691, p-value = 1.421e-14
alternative hypothesis: true mu is not equal to 0
#lmPerm包的置换检验 library(lmPerm) #简单线性回归置换 set.seed(1234) fit<-lmp(weight~height,data=women,perm="Prob") summary(fit)
Call:
lmp(formula = weight ~ height, data = women, perm = "Prob")
Residuals:
Min 1Q Median 3Q Max
-1.7333 -1.1333 -0.3833 0.7417 3.1167
Coefficients:
Estimate Iter Pr(Prob)
height 3.45 5000 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.525 on 13 degrees of freedom
Multiple R-Squared: 0.991, Adjusted R-squared: 0.9903
F-statistic: 1433 on 1 and 13 DF, p-value: 1.091e-14
#多项式回归的置换检验 set.seed(1234) fit<-lmp(weight~height+I(height^2),data=women,perm="Prob") summary(fit)
Call:
lmp(formula = weight ~ height + I(height^2), data = women, perm = "Prob")
Residuals:
Min 1Q Median 3Q Max
-0.509405 -0.296105 -0.009405 0.286151 0.597059
Coefficients:
Estimate Iter Pr(Prob)
height -7.34832 5000 <2e-16 ***
I(height^2) 0.08306 5000 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3841 on 12 degrees of freedom
Multiple R-Squared: 0.9995, Adjusted R-squared: 0.9994
F-statistic: 1.139e+04 on 2 and 12 DF, p-value: < 2.2e-16
#多元回归 library(lmPerm) set.seed(1234) states<-as.data.frame(state.x77) fit<-lmp(Murder~Population+Illiteracy+Income+Frost,data=states,perm="Prob") summary(fit)
Call:
lmp(formula = Murder ~ Population + Illiteracy + Income + Frost,
data = states, perm = "Prob")
Residuals:
Min 1Q Median 3Q Max
-4.79597 -1.64946 -0.08112 1.48150 7.62104
Coefficients:
Estimate Iter Pr(Prob)
Population 2.237e-04 51 1.0000
Illiteracy 4.143e+00 5000 0.0004 ***
Income 6.442e-05 51 1.0000
Frost 5.813e-04 51 0.8627
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.535 on 45 degrees of freedom
Multiple R-Squared: 0.567, Adjusted R-squared: 0.5285
F-statistic: 14.73 on 4 and 45 DF, p-value: 9.133e-08
#单因素方差分析和协方差分析 library(lmPerm) library(multcomp) set.seed(1234) fit<-aovp(response~trt,data=cholesterol,perm="Prob") anova(fit)
Analysis of Variance Table
Response: response
Df R Sum Sq R Mean Sq Iter Pr(Prob)
trt 4 1351.37 337.84 5000 < 2.2e-16 ***
Residuals 45 468.75 10.42
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#双因素方差分析 library(lmPerm) set.seed(1234) fit<-aovp(len~supp*dose,data=ToothGrowth,perm="Prob") anova(fit)
Analysis of Variance Table
Response: len
Df R Sum Sq R Mean Sq Iter Pr(Prob)
supp 1 205.35 205.35 5000 < 2e-16 ***
dose 1 2224.30 2224.30 5000 < 2e-16 ***
supp:dose 1 88.92 88.92 2032 0.04724 *
Residuals 56 933.63 16.67
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#自助法
library(boot)
set.seed(1234)
rsq<-function(formula,data,indices){
d<-data[indices,]
fit<-lm(formula,data=d)
return(summary(fit)$r.square)
}
results<-boot(data=mtcars,statistic=rsq,R=1000,formula=mpg~wt+disp)
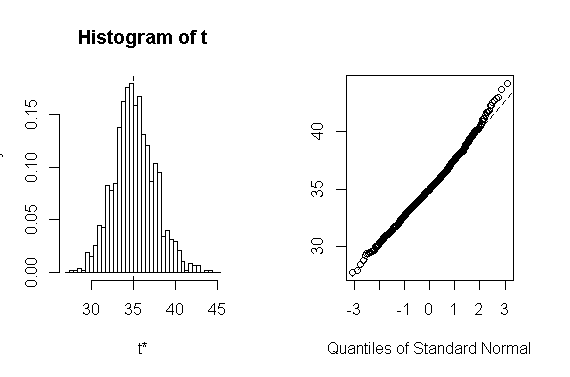
print(results)
boot.ci(results,type=c("perc","bca"))
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 1000 bootstrap replicates
CALL :
boot.ci(boot.out = results, type = c("perc", "bca"))
Intervals :
Level Percentile BCa
95% ( 0.6838, 0.8833 ) ( 0.6344, 0.8549 )
Calculations and Intervals on Original Scale
Some BCa intervals may be unstable
#多个统计量的自助法
bs<-function(formula,data,indices){
d<-data[indices,]
fit<-lm(formula,data=d)
return(coef(fit))
}
library(boot)
set.seed(1234)
results<-boot(data=mtcars,statistic=bs,R=1000,formula=mpg~wt+disp)
print(results)
plot(results,index=1)