机器学习——逻辑回归的原理及python代码实现

机器学习——逻辑回归的原理及python代码实现

逻辑回归的数学原理及推导过程

逻辑回归算法是比较牛的二分算法，是分类用的，机器学习算法中，首选的都是逻辑回归，如果逻辑回归做得好，那还选啥其他的，做的不好再选复杂的。

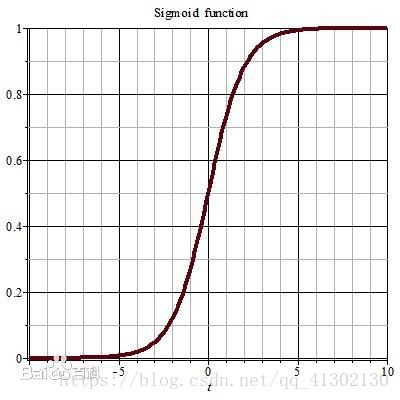
Sigmoid函数方程

1. 方程式如下：
   
   自变量取值为任意实数，值域为[0,1]
   这个方程的目的在于分类，一般用于对两个东西进行分类，也就是分成两类，横轴是任意取值，y轴是这个取值的概率，如果我们算出了这个取值的概率，然后指定一个基准概率，我们就能知道高于这个概率的就是这个类。
   
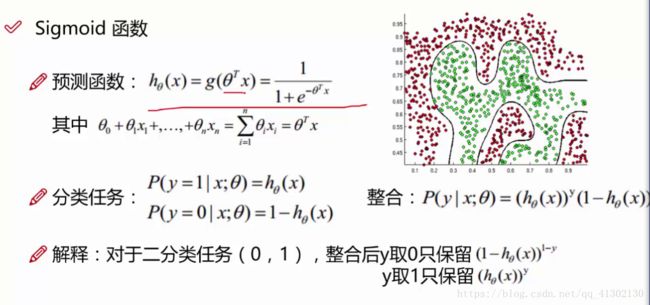
   我们经常把线性回归预测的结果代入到逻辑回归中，用来对线性回归的结果求概率进而进行分类，线性回归的seta可能有 多元，所以是一个矩阵，代入整合后获得概率。意思是在某个seta的情况下，某个x值获得y的概率，这就又变成了求最优seta的问题，在哪个seta下，哪个X下，Y的概率，y值只有两种结果，一种是成功，一种是失败。
   
   接下来求的就是什么样的seta导致在某个x下求出的y的概率最接近真实值，也就是获得这个最大概率，这就是似然函数，自变量是多个seta，最大值偏导数等于 0，就把偏导数求出来，让其等于0，但是这个方程无法直接求解，我们就转换一下 ，用梯度下降的方法求出最小值，反过来就是最大值，这个值也被称之为容忍度。
   
   对于每一个theta都有一个偏导数，梯度下降怎么求极小值呢，就是先求出每个seta的偏导数，然后给定某个seta值，让其不断减去偏导数乘以步长，然后算出新的seta，带入到方程求y值，一直到y值收敛。然后算出每个seta值。
   最后带入线性回归方程，线性回归方程带入逻辑回归方程，这样一个新的方程可以根据样本计算出分类的方程就已经出来了。

python代码实现

导入常用运算类库：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

以下代码写到一半就放弃了，因为较为复杂，写的可以先列出来，真正的代码请看分割线后的：
定义方程：

def sigmoid(z):
    return 1/(1+np.exp(-z))

按照之前的笔记，我们应该把线性回归方程带入到逻辑回归

def model(seta,x):
    return sigmoid(np.dot(seta,x.T))

把数据变成矩阵，并且获取各个x,y的值,seta不知道多少，暂时弄成0

   origin_data=data.as_matrix()
    x = origin_data[:,0:3]
    y =origin_data[:,3:4]
    seta = np.zeros([1,3])
    seta

创建好了x,y后，我们把对数似然函数取负号，然后带入之前的值。

 def cost(X,y,seta):
        left = np.multiply(-y,np.log(model(seta,X)))
        right = np.multiply(1-y,np.log(1-model(seta,X)))
        return np.sum(left -right)/(len(X))

计算梯度，偏导数等于0，我们有三个参数，也要对一共三个参数求梯度

  def gradient(x,y,seta):
        grad = np.zeros(seta.shape)
        error = (model(x,seta)-y).ravel()
        print(error)
        for j in range(len(seta.ravel())):
            term = np.multiply(error,x[:,j])
            grad[0,j] = np.sum(term)/len(x)
        return grad

一切好像如此的顺理成章，根据方程，我们有三个seta,就要算三个偏导数，偏导数就是梯度值，把偏导数放到[0,0,0]的矩阵里，然后先计算括号里面的，为什么 要用ravel呢，因为后面要乘以的xij，用矩阵表示为i是所有的样本数据，j是偏导数seta对应的那一列，所以乘以的是列，所以要把所有减去的数据变成行，才能进行矩阵的乘法。
------------------------------------这里是分割线---------------------------------

运用sklearn去做较为简单，代码如下：

案例目的：给定一堆交易信息，判断交易的结果是否为欺诈交易。

 	from sklearn.preprocessing import StandardScaler
    from sklearn.cross_validation import train_test_split
    from sklearn.linear_model import LogisticRegression
    from sklearn.cross_validation import KFold,cross_val_score
    from sklearn.metrics import confusion_matrix,recall_score,classification_report
    from imblearn.over_sampling import SMOTE

    df = pd.read_csv('creditcard.csv')
    df.head(5)#读取数据，查看结果

对于读出来的数据，先做标准化处理，标准化的目的是因为大部分列都在0附近，结果有一列一两百的值，机器可能会计算错误，为了让他们都在同一个起跑线，对其进行标准化，标准化就是将数据的方差变为1，值在0附近

df['normalAmount']=StandardScaler().fit_transform(df['Amount'].reshape(-1,1))#如果不加reshape则会提示过时，这个-1是让猜一猜第一个维度，我们只指定第二个维度就行
df = df.drop(['Amount','Time'],axis=1)
df.head()

下采样策略和上采样策略的出现的原因，就比如这个数据，不是欺诈的占了25万条，欺诈的才几百条 ，这势必会导致数据不均衡，从而影响数据训练，下采样，是把多的数据弄得跟少的数据一样的少，上采样策略相反

x = df.iloc[:,df.columns != 'Class']#取所有列，包括class列
y = df.iloc[:,df.columns == 'Class']#取所有列，包括class列
number_records_fraud = len(df[df.Class == 1])#获得错误数据的个数
fraud_indices = np.array(df[df.Class == 1].index) #获得错误数据的索引
normal_indices = np.array(df[df.Class == 0].index)#获得class=0正确的索引
normal_indices
#在正常的索引中随机挑选跟错误索引相同个数的索引，然后把这个随机挑选的索引转换成矩阵
random_normal_indices = np.random.choice(normal_indices,number_records_fraud,replace=False)
random_normal_indices = np.array(random_normal_indices)
#把两个索引矩阵，正确和错误的合并起来
under_sample_indices = np.concatenate([fraud_indices,random_normal_indices])
#然后把这些所有数据选出来
under_sample_data = df.iloc[under_sample_indices,:]
under_sample_data.head()
X_undersample = under_sample_data.iloc[:,under_sample_data.columns !=  'Class']
Y_undersample = under_sample_data.iloc[:,under_sample_data.columns == 'Class']
X_undersample.head()

交叉验证，为了确定选择的参数是否准确，交差验证的原理是，把本身拿到的训练数据分成三份，分别叫做1,2,3，先把1和2建立模型，3作为测试数据，然后验证参数到底怎么样，然后2,3作为建立模型，看1作为测试数据，然后以此类推训练三次，这样做可以排除误差。不然如果验证集全是简单的数据会导致模型效果偏高或者偏低。

X_train,X_test,y_train,y_test = train_test_split(X_undersample,Y_undersample,test_size=0.33,random_state=0)
#这样我就拿到了各个矩阵，但是 这次 测试 数据不打算用这个 ，因为太少了，所以把原始数据也这样坐下 
xtrain,xtest,ytrain,ytest=train_test_split(x,y,test_size=0.3,random_state=0)

把新数据和原始数据都切分成训练数据和 测试 数据

在建立模型之前，往往要考虑模型评估标准，以下是精度的含义及为什么精度是骗人的，精度就是，假如在1000个患者样本中，990个正常，10个患了癌症，我的模型只能检测出正常，检测结果发现我的模型正确率是99%,但是这是骗人的，因为我的模型根本检测不出患癌的概率，所以是没有意义的，但是如果用recall（召回率，查全率）计算，10个中一个都没查出来，模型的效率是0除以10等于0，查出一个是10%,这个召回率更好的评价了模型的效果。

关于正则化惩罚项，假设有两组模型，一个是A，一个是B，A和B的seta都能够很好地拟合训练数据，并且recalll值为90%，但是A模型的容忍度浮动较大，B模型的容忍度浮动较小，我们一般会选择B模型，因为A模型浮动较大，可能对测试数据造成过拟合，所谓的过拟合就是对训练数据拟合很好，而对测试数据拟合较差，所以对A的seta进行惩罚，惩罚的标准是给那个函数增加一个1/2的w2,本来浮动大的浮动的更大，浮动小的也浮动大了，然后在对模型进行评估。来计算recall,称之为L2正则化，L1正则化增加W的绝对值，在设置的时候增加惩罚力度，这个系数叫c

def print_Kfold_score(x_train_data,y_train_data):
    fold = KFold(len(y_train_data),5,shuffle=False)#这个的 意思是交叉验证 一共有多少个数据
    c_param_range=[0.01,0.1,1,10,100]#正则化惩罚项的力度
    
    #创建一个表，用来存放不同的c值通过交叉验证所获得的recall的平均值
    result_table = pd.DataFrame(index=range(len(c_param_range)),columns=['C_parameters'])
    j = 0
    result_table['C_parameters'] = c_param_range
    
    for c_param in c_param_range:
        print("--------------")
        print("C_param:"+str(c_param))
        print("------------------------")
        recall_accs = []       #我们要循环遍历每个惩罚力度，看看每个的结果
        for iteration,indices in enumerate(fold,start=1):
            #对于每一个惩罚力度都会有好几个交叉验证，我们看看每个惩罚力度的每一个交叉 验证的结果
            lr = LogisticRegression(C=c_param,penalty='l1')#建立逻辑回归模型，输入惩罚类型和 力度
            lr.fit(x_train_data.iloc[indices[0],:],y_train_data.iloc[indices[0],:].values.ravel())
            #对数据进行训练，这里有一个疑问
            y_pred_undersample = lr.predict(x_train_data.iloc[indices[1],:])
            #交叉验证，必须要选用交叉验证，不然效果不准确，只拟合一个结果的话，可能有 特殊样本，比如 恰好这个c值恰好这个样本好，但是其他四种都是烂的
            recall_acc = recall_score(y_train_data.iloc[indices[1],:],y_pred_undersample)
            #计算recall值，这是模型的评估的直观结果，传入的参数第一个是预测数据的真实值，第二个是预测值
            
            #这段代码的目的是，对于每个c值，我们进行交叉验证，因为交叉验证更准确，进行交叉验证后，获得不同的recall,然后求平均值，选择最好的结果
            recall_accs.append(recall_acc)
            print('Iteration:'+str(iteration)+'     recall  score='+str(recall_acc))
        #全部循环完后得到好几个recall,求平均值放进去
        result_table.loc[j,'result'] = np.mean(np.array(recall_accs))
        j+=1
    best_c = np.max(result_table['result'])
    #全部平均值求完之后，找到最大的 那个平均值，这就是最好的惩罚系数
    c_predict = result_table.loc[result_table['result'] == best_c,'C_parameters']
    print("*"*30)
    print(best_c)
    #c_predict = c_predict.loc[0,'C_parameters']
    print(c_predict)
    return c_predict

以上的代码的意思是我们也不知道正则化惩罚项的惩罚力度，所以我们建立个数组选择一些力度。对每个值进行循环，获取每个值在交叉验证5次后的5个recall，放入数组，最后求recall的平均值，放入新建立的表中，这样就能获得表中每个惩罚力度所对应的recall，然后我们选择值最高的recall，这也就是模型评估最好的那个力度值。

以下的数据结果证明了交叉验证是非常重要的，如果我们不进行交叉验证，我们可能0.01的惩罚因子值可能0.93，而值0.1的惩罚因子值是0.95，这样导致模型运算结果不准确，从而导致选错惩罚因子，从而模型建立就不准确了。所以我们交叉验证5次求平均值，就能够得到正确的惩罚因子，从而得到正确的seta值。比如我在这个惩罚力度下，我的recall还能保持不变，原本我们两个的recall一样 ，现在你的在这个惩罚下就不行了，所以，选我的模型，但是我们选择多少的惩罚力度合适呢，这个方法就是选择最好的惩罚力度。力度过大，大家都不行了

c_predict= print_Kfold_score(x_train_data=X_train,y_train_data=y_train)

调用方法进行测试。
测试结果如下

--------------
C_param:0.01
------------------------
Iteration:1     recall  score=0.985915492958
Iteration:2     recall  score=0.941176470588
Iteration:3     recall  score=1.0
Iteration:4     recall  score=0.971014492754
Iteration:5     recall  score=0.968253968254
--------------
C_param:0.1
------------------------
Iteration:1     recall  score=0.845070422535
Iteration:2     recall  score=0.882352941176
Iteration:3     recall  score=0.949152542373
Iteration:4     recall  score=0.927536231884
Iteration:5     recall  score=0.904761904762
--------------
C_param:1
------------------------
Iteration:1     recall  score=0.859154929577
Iteration:2     recall  score=0.897058823529
Iteration:3     recall  score=0.966101694915
Iteration:4     recall  score=0.942028985507
Iteration:5     recall  score=0.873015873016
--------------
C_param:10
------------------------
Iteration:1     recall  score=0.87323943662
Iteration:2     recall  score=0.882352941176
Iteration:3     recall  score=0.983050847458
Iteration:4     recall  score=0.942028985507
Iteration:5     recall  score=0.888888888889
--------------
C_param:100
------------------------
Iteration:1     recall  score=0.87323943662
Iteration:2     recall  score=0.897058823529
Iteration:3     recall  score=0.983050847458
Iteration:4     recall  score=0.942028985507
Iteration:5     recall  score=0.873015873016
******************************
0.973272084911
0    0.01
Name: C_parameters, dtype: float64

然后将0.01带入，对新数据进行建立模型，然后把旧的测试测试数据 代入预测。

lr = LogisticRegression(C=0.01,penalty='l1')
lr.fit(X_train,y_train.values.ravel())
y_pred = lr.predict(xtest)
#预测值的结果 都是个一维矩阵

#然后画出混淆矩阵
cnf_matrix =confusion_matrix(ytest,y_pred)
#把小数位数改为2位
np.set_printoptions(precision=2)
recall1 = recall_score(ytest,y_pred)
recall2 = cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1])
print(recall1)
print(recall2)
cnf_matrix

输出混淆矩阵结果

0.945578231293
0.945578231293
array([[71435, 13861],
       [    8,   139]])

混淆矩阵的含义，列代表真实值，行代表预测值。recall计算都只看第二行，但是第一行第二个数据，是下采样策略不好的原因，可以看到真实值没问题，但是预测值认为有为题的占了13861个，虽然这个不影响 recall，但是肯定是有问题的，因为误判断的值太多了。
阈值对模型的影响，阈值也就是不按照0.5去计算，这个值是可以更改的，具体怎么更改有方法。

过采样样本生成策略

smote样本生成策略
传进来的是一个训练集的x和训练集的Y

oversampler=SMOTE(random_state=0)
os_x,os_y=oversampler.fit_sample(xtrain,ytrain)
len(xtrain)
len(ytrain)

过样本采集可以很好地避免误判断

综上所述，对于逻辑回归案例的一般解决问题的思路是：

1. 导入数据表，画图观察数据
2. 对数据进行处理，首先可以标准化或者归一化
3. 对数据进行处理，有比较的话进行过采样或者下采样处理
4. 对数据进行切分，获得训练数据和测试数据
5. 利用交叉验证的方法获得recall最高的正则化惩罚力度
6. 建立模型，将上一步的正则化惩罚力度带入，并且选择惩罚类型
7. 对数据进行拟合
8. 获得结果计算recall,画出混淆矩阵
9. 对结果进行分析