数据挖掘实验（一）：混合属性的相似性矩阵 R语言

一、实验内容：

编写代码s=DisFun(T,Sign)，其中T为数据集，Sign为属性类型，d为相似性矩阵

二、源代码：

#num数值型
#fdc表示非对称二元
#dc表示对称二元
#bc表示标称属性
#p表示指示符
#xs表示序数属性

S = function(T,Sign){
  d = data.frame(matrix(NA,nrow(T),nrow(T)))          #相异性矩阵
  distance  = c()    #距离
  p = c()            #指示符
  
  G = T  
  
  
  for(i in 1:nrow(T)){
    for(j in 1:i){
      if(i == j){
        d[i,j]=0
      }
      else{
        
        for(f in 1:ncol(T)){
          if(T[i,f] ==  0&T[j,f] == 0&Sign[f]=='fdc'){
            p[f] = 0
          }
          else if(is.na(T[i,f])|is.na(T[j,f])){
            p[f] = 0
          } 
          else{
            p[f] = 1
          }
          
          
          #相异性计算 
          if(is.na(T[i,f])|is.na(T[j,f])){                                   # xif或xjf缺失
            distance[f] = 0
          }else if(Sign[f]=='num'){                                          #数值型
            distance[f] = abs(T[i,f]-T[j,f])/(max(T[,f])-min(T[,f]))
          }
          else if(Sign[f] =='fdc'|Sign[f] =='dc'|Sign[f] =='bc'){            #标称或者二元（对称和非对称）
            if( T[i,f] == T[j,f]){
              distance[f] = 0
            }else{
              distance[f] = 1
            }
          }
          else if(Sign[f]=='xs'){                                                         #序数型
            
          
            z = (G[,f]-1)/(max(G[,f])-1)
            T[,f] = z       #将原f列替换成映射
             distance[f] = abs(T[i,f]-T[j,f])/(max(T[,f])-min(T[,f]))
          }
          
          
        }
        d[i,j] = round(sum(p*distance)/sum(p),2)
      }
      
    }
  }
  return(d) 
}

#1、书上例子
test1<-c("A","B","C","A")             #标称
test2<-c("优秀","一般","良好","优秀") #序数
test3<-c(45,22,64,28)                 #数值
book_test<-data.frame(test1,test2,test3)
book_test[,2]<-c(3,1,2,3)

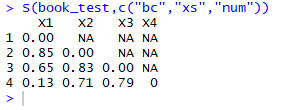
S(book_test,c("bc","xs","num"))

#2、举个栗子
t1 = c(125,48,57,147,58)  #数值
t2 = c("优秀","良好","及格","补考","中等") #序数
t3 = c(1,0,1,1,0)
t4<-c("男","女","女","男","女")
t5 = c("长方形","圆形","三角形","菱形","三角形")

mytest = data.frame(t1,t2,t3,t4,t5)
mytest[,2] = c(5,4,2,1,3)
Sign = c("num","xs","fdc","dc","bc")
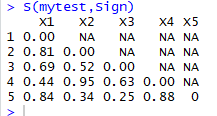
S(mytest,Sign)

三、运行结果：

课本的例子

自己举例