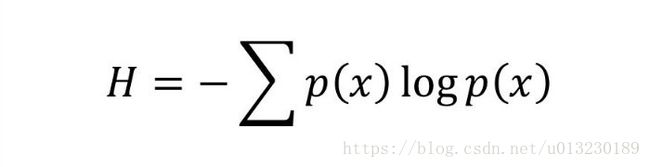机器学习之决策树算法原理详解
微信公众号:数据挖掘与分析学习
在本文中,我们将讨论决策树背后的理论和工作原理。 我们将看到该算法的一些数学知识,即熵和信息增益。
1.动机
假设我们有以下两个类别的图,由黑色圆圈和蓝色方块表示。 是否可以画一条分离线将两个类别分开? 也许没有。
你能花一条线将它们分开吗?
我们需要不止一条线来将上面的类分开。 与下图类似:
我们在这里需要两条线,一条线根据x的阈值分割,另一条线条用于根据y的阈值分割。
现在,你可能已经猜到了决策树是怎么工作的?
决策树分类器通过识别线重复地将工作区域(绘图)划分为子部分。 (重复是因为可能有两个相同类别的距离较远的区域被其他区域划分,如下图所示)
那么划分什么时候会终止呢?
- 它要么分成纯粹的类(只包含单个类的成员)
- 满足分类器属性的一些标准。
在以下部分中,我们定义了与决策树相关的几个术语,然后使用样本示例执行这些计算。
1.不纯度
在上面的划分中,我们明确地进行了分类。 但是,如果我们有以下案例怎么办?
不纯度是指我们将一个类划分为另一个类。 这可能是由于以下原因引起的:
- 我们没有可用的特征来分类。
- 我们容忍一定比例的不纯度(我们停止进一步分割)以获得更快的性能。 (在准确性和性能之间总是存在折衷)。
例如,在第二种情况下,当我们剩下x个更少数量的元素时,我们可以停止我们的划分。 这也称为基尼不纯度。
2.熵
熵是元素的随机性程度,换句话说,它是不纯度的量度。 在数学上,它可以借助于变量的概率来计算:
P(x)是变量x的概率
| 举例说明: 在投掷骰子的实验中,总共进行了四次投掷,骰子的面数分别为1,1,2,3,则: p(1) = 0.5 p(2) = 0.25 p(3) = 0.25 entropy = - (0.5 * log(0.5)) - (0.25 * log(0.25)) -(0.25 * log(0.25) = 0.45 |
3.信息增益
假设我们有多个特征来划分当前数据集。 我们应该选择什么特征来进行划分? 或许可以减少不纯度。假设我们将类划分为多个分支,如下所示,任何节点的信息增益定义为:
Information Gain (n) = Entropy(x) — ([weighted average] * entropy(children for feature)) |
解释一下:
假设我们有以下类别:
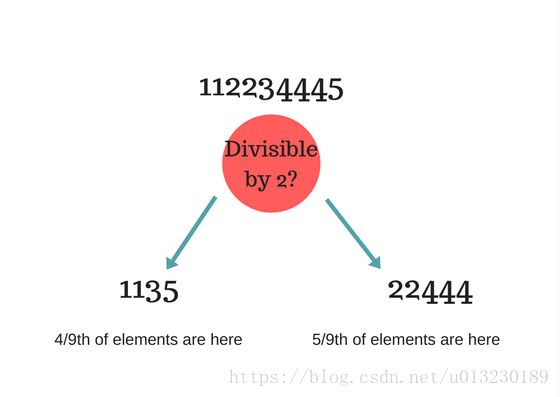
112234445
我们基于以下属性来划分:是否能被2整除?
Entropy at root level : 0.66 Entropy of left child : 0.45 , weighted value = (4/9) * 0.45 = 0.2 Entropy of right child: 0.29 , weighted value = (5/9) * 0.29 = 0.16 Information Gain = 0.66 - [0.2 + 0.16] = 0.3 |
如果我们使用是否为素数而不是能否被2整除来决策,那么检查我们得到了什么信息。哪一种更适合这种情况?
决策树在每个阶段选择最佳的信息增益的特征。表示该特征根本不会分割数据集。
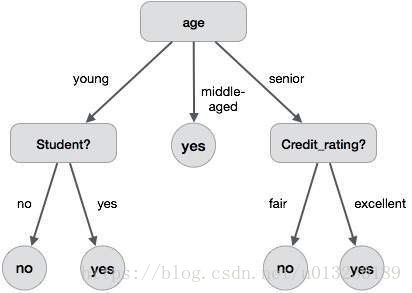
4.实例
现在您已经了解了关于决策树的基本知识,让我们解决一些示例,看看它是如何工作的。
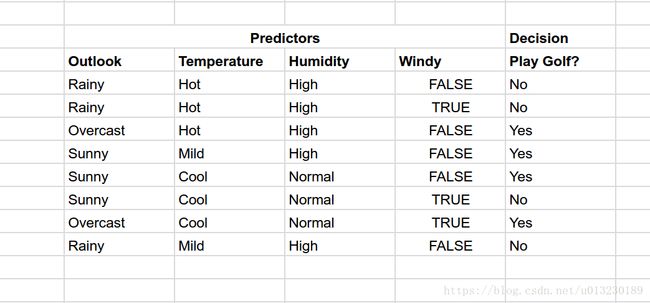
假设我们有以下数据关于可以在各种条件下打高尔夫球。
现在,如果天气状况如下:
| Outlook : Rainy, Temperature: Cool, Humidity: High, Windy: False |
那么是否应该去打高尔夫?
数据集结果是:NNYYYNYN,则计算可得根节点信息熵为:0.3。
根据特征outlook, temperature, humidity and Windy来选择最好的划分:
举例:如果根据outlook来划分:
Rainy : NNN (entropy = 0) Sunny : YYN (entropy = 0.041) Overcast : YY (entropy = 0) |
所以信息增益为:information gain = 0.3 - [0 + (3/8)*0.041 + 0]
= 0.28
通过计算其他的特征的信息增益可知当根据outlook来划分时信息增益最大。
对于outlook来说,Rainy对应的多是N(不打高尔夫)和overcast对应的都是Y(打高尔夫),不纯度为0,因此,我们根据Sunny来划分:
Sunny
YYN
Windy? Yes : N
No : YY
所以预测结果为:
Outlook : Rainy, Temperature: Cool, Humidity: High, Windy: False
基于最大信息增益有效划分是决策树分类器的关键。 然而,在现实世界中,数百万个数据在实际上不可能划分为纯类(可能需要更长的训练时间),因此当满足某些参数(例如不纯度百分比)时,我们停止划分。
翻译:
https://medium.com/machine-learning-101/chapter-3-decision-trees-theory-e7398adac567