常见平衡树（2-3树与红黑树原理与实现）

原文地址：https://kswapd.cn/article/twothreetree-and-rbtree/

本文介绍下两种常见的平衡树，2-3树和红黑树，这两种树在工业级代码中有广泛的应用。
其中红黑树可以看成是2-3树的进化版本，理解2-3树后，对理解红黑树的平衡过程很有帮助，所以建议大家按照顺序阅读。

2-3树

计算机科学中，2–3树是一种树型数据结构，内部节点（存在子节点的节点）要么有2个孩子和1个数据元素，要么有3个孩子和2个数据元素，叶子节点没有孩子，并且有1个或2个数据元素。2–3树由约翰·霍普克洛夫特于1970年发明。

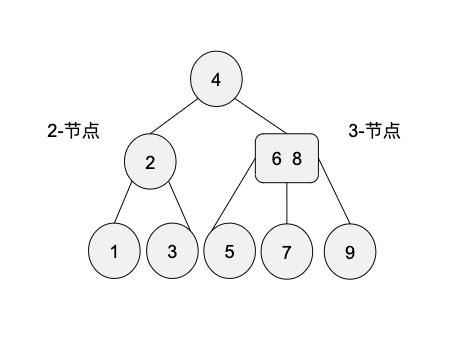
如下图三节点和二节点并存的树称为2-3树。

2-3树的性质

2-3树的性质是能够自平衡的关键。

1. 一颗2-3树由2-节点和3-节点组成。
2. 2-节点含有一个键和两个子节点，所有左子节点的键均小于该2-节点，右子节点的键均大于该2-节点。
3. 3-节点含有两个键和三个子节点，所有左子节点均小于该3-节点的左键，所有右子节点均大于该3-节点的右键，中子节点的大小在左右键之间。

插入过程

向2-节点中插入新键

在节点中插入，将这个2-节点变成3-节点即可。

向一颗只含有3-节点的树中插入新键

1. 先将数据临时存储在3-节点中，这时该节点会变成4-节点。
2. 将该4-节点分解成三个2-节点组成的二叉查找树，即中键是父节点，左右键分别是左右子节点。

向一个父节点为2-节点的3-节点中插入新键

1. 将新键插入到3-节点中，此时3-节点变成4-节点。
2. 将4-节点的中键移动到父节点中，此时父节点变成3-节点。
3. 并将原来的2-节点分解成该父节点的左右两个子节点。

分解根节点

如果出现4-节点一直向上分解的情况，直到根节点，那么将触发根节点分解。
此时根节点必为4-节点，直接分解为三个2-节点，此时树高度加1。

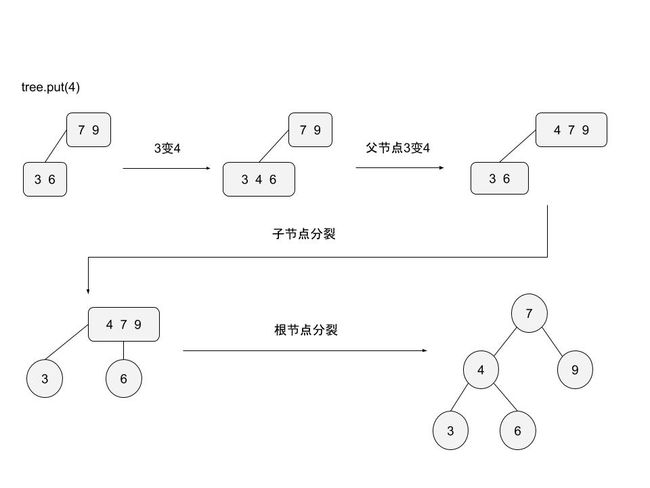
向一个父节点为3-节点的3-节点中插入新键

1. 将新键插入到3-节点中，此时3-节点变成4-节点。
2. 将该4-节点的中键插入父节点中，此时父节点也变成4-节点，此时原节点变成3-节点。
3. 将原3-节点分解成父节点的左右两个子节点。
4. 将父节点看做原节点，重复2-4过程，直到遇到父节点是2节点，不用再继续向上分解。

树节点定义

2-3树中两种类型的树节点，这里我们为了方便，就用一个结构来表示2-节点和3-节点了。
这里的key和children都是有序的，比如用1，2，3分别表示左，中，右键，左，中，右孩子节点。
使用这个needSplit方法表示是否需要分裂，如果该节点的键数大于2，就是成为4-节点，那么就需要分裂，我们后面会将分裂实现。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

/** * 2-3树节点，这里把2-节点和3-节点都放在一起了 */ class Node {       private Node parent = null;     // 该节点保存的数据     private final List keys = new ArrayList<>();     // 子节点     private final List children = new ArrayList<>();       /**      * 向节点中插入元素，2-3树无法向下增长，需要在当前节点插入后向上分裂      *      * @param num      */     public void insert(int num) {         keys.add(num);         Collections.sort(keys);     }       public boolean isLeaf() {         return children.isEmpty();     }       /**      * 需要分裂      *      * @return true/false      */     public boolean needSplit() {         return keys.size() > 2;     } }

查找实现

2-3树的查找实现比二叉树复杂一点，因为需要考虑三节点的情况。不过依然是一个递归的过程。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

private Node search(Node start, int key) {     if (mRoot == null) {         return null;     }     // 找到直接返回     if (start.keys.contains(key)) {         return start;     }     if (start.isLeaf()) {         return null;     }     int keyCount = start.keys.size();     if (key < start.keys.get(0)) {         // 查找左节点         return findInsertNode(start.children.get(0), key);     } else if (key > start.keys.get(keyCount - 1)) {         // 查找右节点         // 根据2-3树的定义，右节点一定是keyCount         return findInsertNode(start.children.get(keyCount), key);     } else {         // 查找中间节点         // 这个时候1代表的是2-3树的中间节点         return findInsertNode(start.children.get(1), key);     } }

插入实现

插入的过程就比较复杂了，涉及到向上分裂，我们先看下插入，插入的话这里我们直接把键放到树节点里即可，然后判断它是否需要分裂。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

/** * 向2-3树中插入节点 * * @param key key * @return true 成功 false 失败 */ public boolean put(int key) {     if (mRoot == null) {         mRoot = new Node();         mRoot.insert(key);         return true;     }     final Node insertNode = findInsertNode(mRoot, key);     if (insertNode == null) {         return false;     }     insertNode.insert(key);     if (insertNode.needSplit()) {         split(insertNode);     }     return true; }

每个节点插入后都是根据needSplit方法判断是否需要分裂的。

分裂过程如下：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70

/** * 当前节点向上分裂，2-3树保持平衡的核心 * * @param pivot 需要分裂的节点 */ private void split(Node pivot) {     if (pivot == null) {         return;     }     Node parent = pivot.parent;     // 中间键     int middle = pivot.keys.get(1);     // 新分裂的节点     Node n2 = new Node();       // 开始分裂     if (pivot.isLeaf()) {         /*             此时是叶子节点分裂，初始分裂状态一定是根节点         */           // n2 获取右键         n2.keys.add(pivot.keys.get(2));         // 原节点删除右键和中键         pivot.keys.remove(2);         pivot.keys.remove(1);     } else {         /*             此时是中间节点分裂，这个状态一般是叶子节点分裂完后出现的。         */           // n2 获取后两个键，注意添加顺序         n2.children.add(pivot.children.get(2));         n2.children.add(pivot.children.get(3));           // 删除两个孩子         pivot.children.remove(3);         pivot.children.remove(2);           n2.keys.add(pivot.keys.get(2));         n2.children.get(0).parent = n2;         n2.children.get(1).parent = n2;           // 原节点删除右键和中键         pivot.keys.remove(2);         pivot.keys.remove(1);     }       // 分裂根节点     if (parent == null) {         mRoot = new Node();         mRoot.parent = null;         mRoot.children.add(pivot);         mRoot.children.add(n2);           // root 节点取中间键         mRoot.keys.add(middle);         pivot.parent = mRoot;         n2.parent = mRoot;     } else {         // 把当前分类的n2插入到父节点的孩子节点中         int indexInParent = pivot.parent.children.indexOf(pivot);         pivot.parent.children.add(indexInParent + 1, n2);         pivot.parent.insert(middle);         n2.parent = parent;         if (parent.needSplit()) {             split(parent);         }     } }

分裂过程就是上面图中总结的几个步骤，不详细解释了，大家可以结合注释看下，2-3树的插入过程比红黑树复杂很多，有大量的指针操作，我也是费了很长时间才完成。

生成过程

我们测试下刚才的2-3树代码，采用一个顺序序列，看看2-3树能不能实现平衡。
测试代码如下:

1 2 3 4 5 6 7 8 9 10 11 12

public static void main(String[] args) {     TwoThreeTree tree = new TwoThreeTree();     tree.put(1);     tree.put(2);     tree.put(3);     tree.put(4);     tree.put(5);     tree.put(6);     tree.put(7);     tree.put(8);     tree.put(9); }

接下来我们来画图分析下生成过程。绘图工具用的Google Drawing，如果大家需要，我可以把原图分享出来。

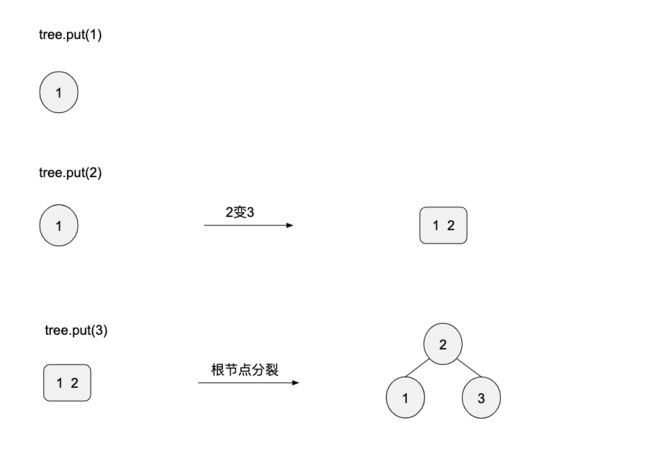
插入1-3节点的过程：
2-3树的插入之前也说过，不是向下增长的，是将要插入的键停留到当前节点中，然后向上分裂，我们可以看到插入3的时候触发了一次根节点分裂。

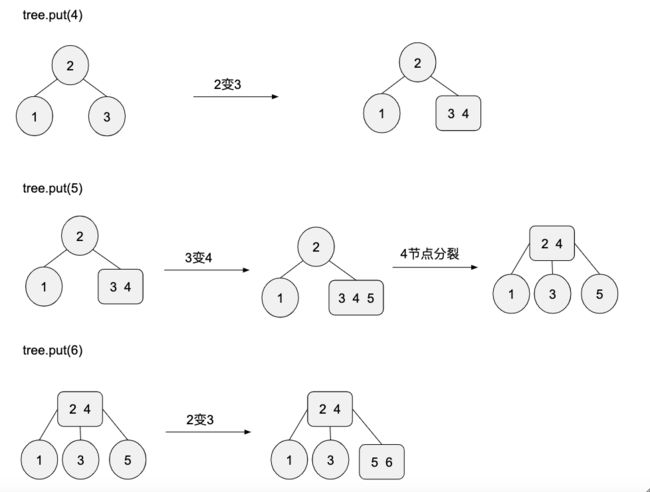
插入4-6节点的过程:
跟原来的逻辑一样，如果节点变成4-节点，那么就向上分裂。

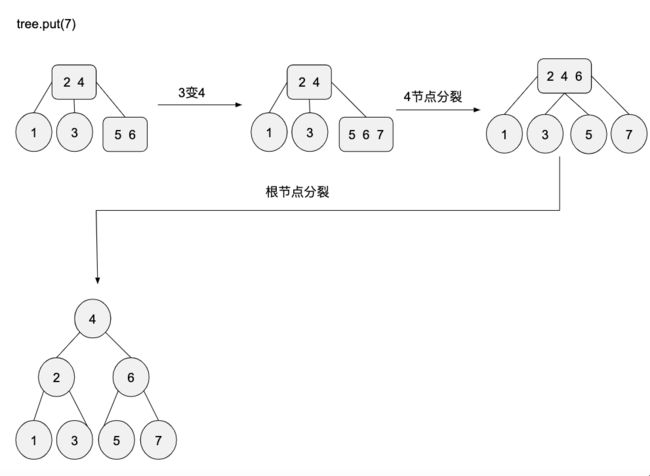
插入7节点的过程：
这个过程比较复杂，下面重点说下，当我们准备插入7节点时，查找到的位置是（5-6）节点，这已经是一个3-节点了，我们在这个节点插入势必会触发分裂。
插入后（5-6-7）节点向上分裂，6键上移，5，7分别分裂中左右子节点，这时上移插入到父节点导致父节点也变成3-节点，继续触发分裂，4节点上移成根节点，2，6分别变成左右子节点。

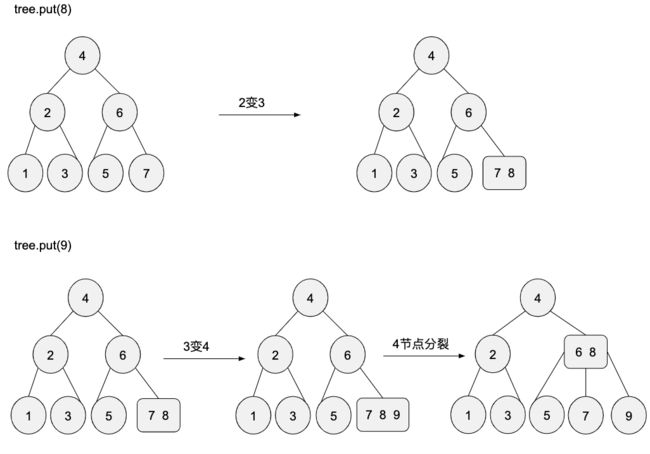
插入8-9节点的过程：
这个就是很普通的插入-分裂逻辑了，上面已经涵盖过了，不再啰嗦。

生成完后，我们看下这个2-3树明显比BST要平衡很多，查找的性能也会好很多。

完整代码实现

我已将完整代码上传到github，大家可以参考实现下。

github-gist-TwoThreeTree

红黑树

红黑树（英语：Red–black tree）是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。它在1972年由鲁道夫·贝尔发明，被称为”对称二叉B树”，它现代的名字源于Leo J. Guibas和Robert Sedgewick于1978年写的一篇论文。红黑树的结构复杂，但它的操作有着良好的最坏情况运行时间，并且在实践中高效：它可以在 O(log(n))时间内完成查找，插入和删除，这里的 n是树中元素的数目。

红黑树的平衡规则

1. 节点是红色或者黑色。
2. 根节点是黑色。
3. 每个叶子节点都是黑色的空节点（NIL）。
4. 每个红节点的子节点都是黑节点，即任何路径上不能连续出现两个红节点。
5. 从任意节点到每个叶子节点都包含相同数目的黑色节点。（黑色平衡）

红黑树的调整方法/插入过程

红黑树的处理过程是与2-3树类似，是自下而上进行生长，在向上生长的过程中，需要通过左旋，变色，右旋的来不断将树的节点进行调整，维持树的高度，达到平衡。

同时，为了方便调整，我们假设所有新插入的节点在调整之前均为红色。

左旋

如果当前节点的右节点是红色，左节点是黑色，那么当前节点需要左旋。
举例说下左旋的应用场景。

这个比较典型的情况是在根节点插入一个大于自己的键的情况下，即当前节点小于要插入的节点。如本例中

1 2	rbTree.put(3); // 已成为根节点 rbTree.put(4); // 插入一个比自己大的节点

会触发左旋。

左旋的java实现

1 2 3 4 5 6 7 8 9 10 11

private static Node rotateRight(Node pivot) {     Node newPivot = pivot.left;       newPivot.left = pivot.right;     pivot.right = newPivot;       newPivot.color = pivot.color;     pivot.color = RED;       return newPivot; }

变色

如果当前节点的左右两个子节点皆为红色的话，那么会触发变色逻辑，如下例。

我们看下变色的Java实现。

1 2 3 4 5 6

private static Node flipColor(Node pivot) {     pivot.color = RED;     pivot.left.color = BLACK;     pivot.right.color = BLACK;     return pivot; }

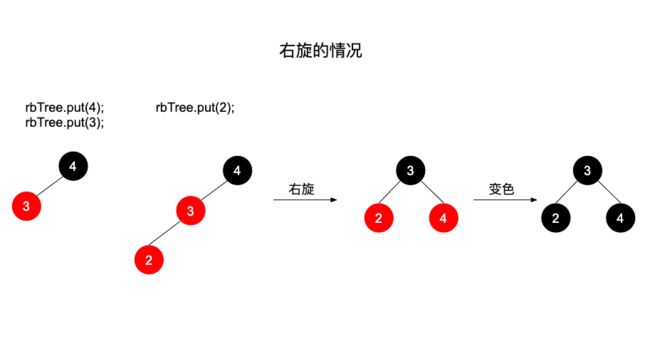
右旋

右旋比较复杂，一般伴随有变色和左旋，变色和左旋前面已经介绍过了，我们看下出现右旋的情况。
如果当前基准节点的左子节点和左孙子节点（左子节点的左子节点）都为红色，此时违反了红黑树平衡原则的第四条，此时我们需要右旋解决这种情况。

我们看下右旋的Java实现

1 2 3 4 5 6 7 8 9 10 11

private static Node rotateRight(Node pivot) {     Node newPivot = pivot.left;       newPivot.left = pivot.right;     pivot.right = newPivot;       newPivot.color = pivot.color;     pivot.color = RED;       return newPivot; }

树节点定义

与二叉树的节点相比只多了个颜色字段，表示红或者黑。

1 2 3 4 5 6 7

// get/set省略 class Node {     int key;     boolean color;     Node left;     Node right; }

插入代码实现

红黑树的插入和BST的插入很像，只不过多了个修复的过程，这个修复根据上面所说的基础操作来维持红黑树的平衡。

BST的插入操作

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

private Node put(Node node, int key) {     if (node == null) {         return new Node(key, RED);     }     if (key == node.key) {         node.key = key;     }     boolean cmp = key < node.key;     if (cmp) {         node.left = put(node.left, key);     } else {         node.right = put(node.right, key);     }     return node; }

递归的寻找左右子节点进行插入，我们不多介绍了，看下红黑树的版本。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

/** * 向指定Node中插入节点 * * @param node 从哪个节点开始插入 * @param key  要插入的key * @return 该节点插入的位置 */ private Node put(Node node, int key) {     if (node == null) {         return new Node(key, RED);     }     if (key == node.key) {         node.key = key;     }     boolean cmp = key < node.key;     if (cmp) {         node.left = put(node.left, key);     } else {         node.right = put(node.right, key);     }     // 根据红黑树规则修复     node = fixupAfterPut(node);     return node; }

看到了吧，多个个fixupAfterPut方法，这个方法就是将红黑树修复平衡的。
我们看下实现，其实就是借助上上面的旋转和变色，然后依赖递归将基准节点逐渐向上转移，最后到根节点。
这个过程也足以证明红黑树的自下向上生长的。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

private Node fixupAfterPut(Node node) {     /*         对插入后的树进行修复     */       // 不需要处理的情况： 当前节点为黑色，新元素插入到左子节点。       // 需要处理的情况，按照如下规则:     // 规则一：如果出现红色右子节点，黑色左子节点     if (isRed(node.right) && !isRed(node.left)) {         // 相对父节点进行旋转         node = rotateLeft(node);     }       // 规则二： 如果当前子节点和孙子节点是红色，那么以子节点为基准右旋并且变色     if (node.left != null && isRed(node.left) && isRed(node.left.left)) {         rotateRight(node.left);     }       // 规则三：如果出现该节点同时红色左子节点和右子节点，那么进行变色，将左右子节点变黑，当前节点变红。     if (isRed(node.left) && isRed(node.right)) {         flipColor(node);     }     return node; }

查找

红黑树的查找过程与BST一致，这里我简单写个递归版本。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

/** * 查找操作/与BST相同 * * @param key 要查找的key * @return node 节点 */ public Node search(Node start, int key) {     if (start == null) {         return null;     }     if (key == start.key) {         return start;     }     if (key > start.key) {         return search(start.right, key);     } else {         return search(start.left, key);     } }

生成过程

看完了红黑树的平衡过程后，我们一起来看下在插入极端数据(1,2,3,4,5,6,7,8,9)的情况下，二叉树是如何保持平衡的。
我们一次向树中插入一个顺序序列，这个序列对BST能造成最大程度的破坏，使BST能够变成一个线性结构，我们看下红黑树的表现如何。
测试代码如下:

1 2 3 4 5 6 7 8 9 10 11 12

public static void main(String[] args) {     RBTree rbTree = new RBTree();     rbTree.put(1);     rbTree.put(2);     rbTree.put(3);     rbTree.put(4);     rbTree.put(5);     rbTree.put(6);     rbTree.put(7);     rbTree.put(8);     rbTree.put(9); }

接下来我们以图片来演示下红黑树的平衡过程。

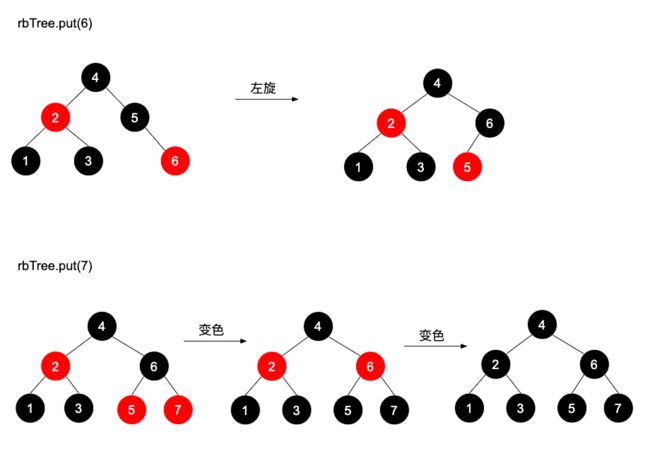
向节点中插入1-3的过程，这个时候涉及到创建根节点，左旋。

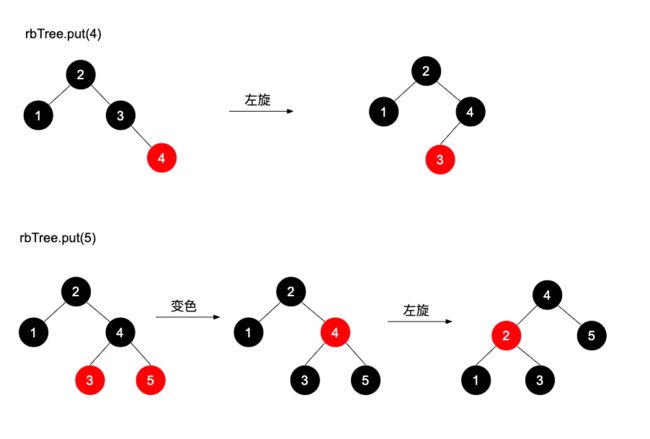
然后是插入4-5节点的过程，插入4时，4是3的右红子节点，所以需要以3为基准进行左旋；
插入5节点时，3和5节点均为红色，所以需要以4为基准进行变色，变完色后发现4又是2的右红子节点，所以又需要以2为基准左旋。

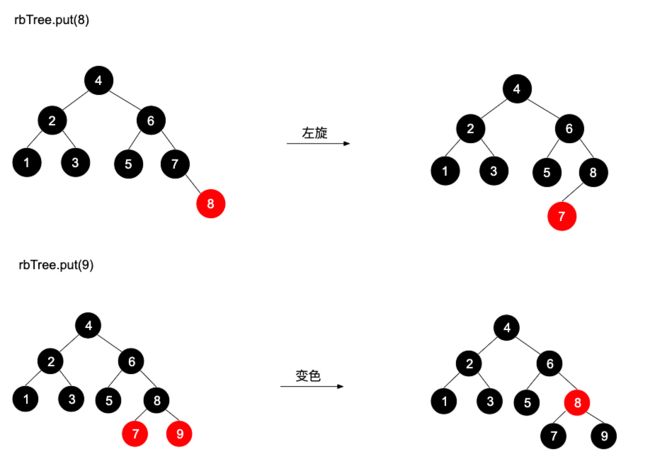
接下来是插入6-7节点，插入6节点时需要左旋，原因跟上面一样，不多解释；
插入7节点时，5，7节点均为红色，需要向上变色，变完色后，发现2，6节点均为红色，接着向上变色，但是上面是根节点了，强制变为黑色。
于是整个数都变成黑色的了，不要觉得奇怪，它仍然满足红黑树上面的5条性质。

最后是插入8-9节点的过程，插入8节点时触发左旋，插入9节点时触发变色。

红黑树到这里就生成完了，我们可以看到，在每一步时，都满足红黑树的5条平衡性质。
我们来对比下BST的生成树和红黑树的生成树，可以看出红黑树明显比BST矮了很多，而BST已经退化成线性结构了，查找的时间复杂度分别为O(n)和O(logn)。

完整代码

我把这个代码实现放到github上了，如果大家有兴趣可以看下。
github-gist-RBTree

2-3树与红黑树对比

2-3树和红黑树都有良好的平衡性，但是2-3树的实现实在太过复杂，并且需要频繁的创建新节点（分裂），所以后来几乎都用红黑树来代替2-3树了，红黑树对平衡的要求没有那么严格，但是代码较为简单清晰（相比其他平衡树），所以在计算机的领域有着广泛的应用。

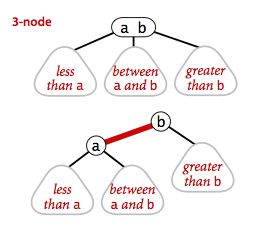
红黑树其实是起源于2-3树的，把红黑树的每个红链接（节点）画平，可以看出它就是一个2-3树，它是用左旋，右旋，变色这三种基础操作代替了2-3树向上分裂的过程。

借算法的一张图，说明下这个结论。

最后

算上画图和代码实现，这篇文章写了很长时间（大约一周了），但是还是有很多逻辑没有介绍到，比如这两个树的删除操作，删除操作是插入的逆过程，比插入还要复杂，如果后面有时间我再写一篇文章介绍吧。

希望大家看了能有收获，有什么问题或没看懂的地方可以在下方留言，我会及时回复:-)

参考资料

算法原理系列：红黑树
查找（一）史上最简单清晰的红黑树讲解