机器学习实战—使用Apriori算法进行关联分析

从大规模数据集中寻找物品间的隐含关系被称作关联分析或者关联规则学习。

一、关联分析

频繁项集：经常出现在一块的集合。
关联规则：按时两种物品之间可能存在很强的关系。

支持度：一个项集的支持度被定义为数据集中包含该项集的记录所占的比例。
可信度或置信度：是针对诸如{尿布}—>{葡萄酒}的关联规则来定义的，这条规则的可信度被定义为：支持度（{尿布，葡萄酒}）/支持度（{尿布}）

支持度和可信度是用来量化关联分析是否成功的方法。

二、Apriori原理
Apriori原理可以帮我们减少可能感兴趣的项集，Apriori原理是说如果某个项集是频繁的，那么它的所有子集也是频繁的，反过来，如果一个项集是非频繁集，那么它的所有超集也是非频繁集。使用Apriori原理可以避免项集数目的指数增长。

三、使用Apriori算法来发现频繁集
关联分析的目标包括两项：发现频繁项集和发现关联规则，首先需要先找到频繁项集，然后才能获得关联规则。

Apriori算法的两个输入参数分别是最小支持度和数据集，该算法首先会生成所有单个物品的项集列表，接着扫描交易记录来查看哪些项集满足最小支持度要求，那些不满足最小支持度的集合会被去掉。然后，对生下来的集合进行组合以生成包含两个元素的项集，接下来，再重新扫描交易记录，去掉不满足最小支持度的项集。该过程重复进行，知道所有项集都被去掉。

1.生成候选项集
数据集扫描的伪代码：
对数据集中的每条交易记录
对每个候选项集：
检查一下候选项集是否是记录条的子集：
如果是，则增加候选集的计数值
对每个候选项集：
如果其支持度不低于最小值，则保留该项集
返回所有频繁项集列表

Aprioiri函数算法中的辅助函数：

#加载数据函数
def loadDataSet():
    dataList = [[1,3,4],[2,3,5],[1,2,3,5],[2,5]]
    #将列表数据映射为集合返回
    return dataList

#创建初始情况下只包含一个元素的候选项集集合
def createC1(dataSet):
    #定义候选项集列表C1
    C1 = []
    #遍历数据集合，并且遍历每一个集合中的每一项，创建只包含一个元素的候选项集集合
    for transaction in dataSet:
        for item in transaction:
            #如果没有在C1列表中，则将该项的列表形式添加进去
            if not [item] in C1:
                C1.append([item])
    #对列表进行排序
    C1.sort()
    # print("C1 not frozenset:",C1)
    #将C1冰冻，即固定列表C1，使其不可变
    return list(map(frozenset,C1))

#创建满足支持度要求的候选键集合
def scanD(D,ck,minSupport):
    #定义存储每个项集在消费记录中出现的次数的字典
    ssCnt = {}
    #遍历这个数据集，并且遍历候选项集集合，判断候选项是否是一条记录的子集
    #如果是则累加其出现的次数
    for tran in D:
        for scan in ck:
            if scan.issubset(tran):
                if not scan in ssCnt:
                    ssCnt[scan] = 1
                else:
                    ssCnt[scan] +=1
    #计算数据集总及记录数
    # print("ssCnt:",ssCnt)
    numItems = float(len(D))
    #定义满足最小支持度的候选项集列表
    retList = []
    #用于所有项集的支持度
    supportData = {}
    #遍历整个字典
    for key in ssCnt:
        #计算当前项集的支持度
        support = ssCnt[key]/numItems
        #如果该项集支持度大于最小要求，则将其头插至L1列表中
        if support >= minSupport:
            retList.insert(0,key)  #添加的是key，不是ssCnt
        #记录每个项集的支持度
        supportData[key] = support
    return retList,supportData

注：frozenset类型是指被“冰冻”的集合，就是说它们是不可变的，用户不能修改它们，这里必须使用frozenset类型而不是set类型，因为之后必须要将这些集合作为字典键值使用，使用frozenset可以实现这一点，而set却做不到。

2.组织完整的Apriori算法

整个Apriori算法的伪代码如下：
当集合项中的个数大于0时
构建一个k个项组成的候选项集的列表
检查数据以确认每个项集都是频繁的
保留频繁项集并构建k+1项组成的候选项集列表

Apriori算法

#上述函数创建了L1，则现在需要创建由L1->C2的函数，也就是说需要将每个项集集合元素加1
#并且迭代这个过程，完成所有频繁项集的查找
#首先完成由(Lk-1)->(Ck)的过程
def aprioriGen(lkPri,k):
    #存储Ck的列表
    retList = []
    #获取lkPri长度，便于在其中遍历
    lkLen = len(lkPri)
    #两两遍历候选项集中的集合
    for i in range(lkLen):
        for j in range(i+1,lkLen):
            #因为列表元素为集合，所以在比较前需要先将其转换为list,选择集合中前k-2个元素进行比较，如果相等，则对两个集合进行并操作
            #这里可以保证减少遍历次数，并且可保证集合元素比合并前增加一个
            L1 = list(lkPri[i])[:k-2]
            L2 = list(lkPri[j])[:k-2]
            #对转化后的列表进行排序，便于比较
            L1.sort()
            L2.sort()
            if L1 == L2:
                #对两个集合进行并操作
                retList.append(frozenset(lkPri[i])|frozenset(lkPri[j]))
    return retList  #[{},{},{}]

#生成所有频繁项集函数
def apriori(dataSet,minSupport=0.5):
    #创建C1
    C1 = createC1(dataSet)
    #对数据集进行转换，并调用函数筛选出满足条件的项集
    D = list(map(set,dataSet))
    #!!!!!!!!!!!!scanD(D,C1,minSupport)函数返回值有两个，一定要用两个值接受
    L1, supportData = scanD(D,C1,minSupport)
    #定义存储所有频繁项集的列表
    L = [L1]
    k = 2
    #迭代开始，生成所有满足条件的频繁项集（每次迭代项集元素个数加1）
    #迭代停止条件为，当频繁项集中包含了所有单个项集元素后停止
    while (len(L[k-2])>0):
        Ck = aprioriGen(L[k-2], k)
        Lk,supK = scanD(D,Ck,minSupport)
        #更新supportData
        #不断的添加以项集为key，以项集的支持度为value的元素
        # 将此次迭代产生的频繁集集合加入L中
        L.append(Lk)
        supportData.update(supK)
        k += 1
    return L,supportData

注：上面的k-2有点让人迷惑。下面解释一下。当利用{0}、{1}、{2}构建{0，1}、{0，2}、{1，2}时，这实际上是将单个项组合到一块，现在如果想利用{0，1}、{0，1}、{1，2}来创建三元素项集，如果将每两个集合合并，就会得到{0，1，2}、{0，1，2}、{0，1，2}，也就是说同样的结果集合会重复3次。接下来需要扫描三元素项集列表来得到非重复结果，我们要确保遍历列表的次数最少。现在，如果比较集合{0，1}、{0，2}、{1，2}的第一个元素并只对第一个元素相同的集合求并操作，会得到{0，1，2}，而且只有一次操作，这样就不需要遍历列表来寻找非重复值。

四、从频繁集中挖掘关联规则

对于关联规则，其量化指标为可信度，可信度的计算公式再前面已经提过，这里不再赘述，为找到感兴趣的规则，我们先生成一个可能的规则列表，然后测试每条规则的可信度，如果该规则的可信度不满足最小可信度要求，则去掉该规则。

关联分析的两个重要目标是发现频繁项集与关联规则。要找到关联规则，首先从一个频繁项集开始，集合中的元素是不重复的，但我们想知道基于这些元素能否获得其他内容。某个元素或者某个元素集合可能会推导出另一个元素。例如，一个频繁项集{豆奶, 莴苣}，可能有一条关联规则“豆奶→莴苣”，箭头的左边集合称作前件，箭头右边的集合称为后件。

每个频繁项集可产生许多关联规则，如果能够减少规则数目来确保问题的可解性，那么计算起来会好很多。如果某条规则并不满足最小可信度要求，那么该规则的所有子集也不会满足最小可信度要求。利用此性质来减少测试的规则数目，可以先从一个频繁项集开始，接着创建一个规则列表，其中规则右部只包含一个元素，然后对这些规则测试。接下来合并所有剩余规则来创建一个新的规则列表，其中右部包含两个元素。这种方法称为分级法

关联规则生成函数：

#生成关联规则列表[(前件,后件,可信度)]
def generateRules(L,supportData,minConf=0.7):
    bigRuleList = []
    #遍历整个频繁集列表
    for i in range(len(L)):
        #遍历每个频繁集
        for freqSet in L[i]:
            #将频繁集转换为包含频繁集中单个元素的列表,单个整数不能用frozenset（）函数，所以这里使用frozenset([item])
            #此处保存规后件元素
            H1 = [frozenset([item]) for item in freqSet]
            #如果频繁集元素个数大于2,则将H1合并
            if i>1:
                #此函数对规则后件进行合并，创建出多条候选规则，在此函数中计算规则可信度，并将满足可信度的规则加入列表中
                #递归创建可能出现的规则
                rulesFromConseq(freqSet,H1,supportData,bigRuleList,minConf)
            else:
                #如果频繁集元素只有两个则直接计算可信度
                calcConf(freqSet,H1,supportData,bigRuleList,minConf)
    return bigRuleList

def calcConf(freqSet,H,supportData,br1,minConf):
    #用于存储满足可信度要求的规则后件集合列表
    prunedH = []
    #H表示规则后件的元素集合列表，遍历后件集合列表
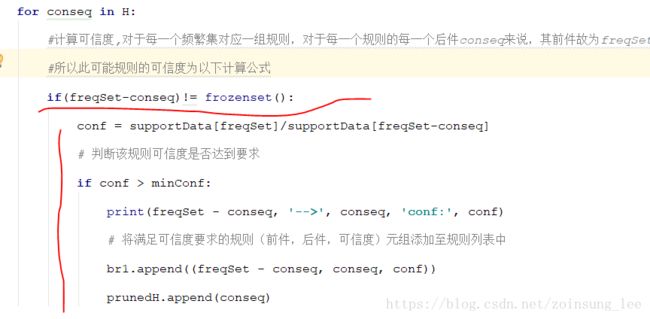
    for conseq in H:
        #计算可信度,对于每一个频繁集对应一组规则，对于每一个规则的每一个后件conseq来说，其前件故为freqSet-conseq
        #所以此可能规则的可信度为以下计算公式
        if(freqSet-conseq)!= frozenset():
            conf = supportData[freqSet]/supportData[freqSet-conseq]
            # 判断该规则可信度是否达到要求
            if conf > minConf:
                print(freqSet - conseq, '-->', conseq, 'conf:', conf)
                # 将满足可信度要求的规则（前件，后件，可信度）元组添加至规则列表中
                br1.append((freqSet - conseq, conseq, conf))
                prunedH.append(conseq)
    return prunedH

#对规则后件进行合并，以此生成后件有两元素的规则，有三元素的规则....
def rulesFromConseq(freqSet,H,supportData,br1,minConf):
    #获取后件元素的个数
    m = len(H[0])
    #如果频繁集元素个数大于规则后件个数
    if(len(freqSet) > (m+1)):
        #先将后件元素合并为元素大于当前元素数1
        Hmp1 = aprioriGen(H,m+1)
        #通过calcConf()获得满足可信度要求的后件元素列表
        Hmp1 = calcConf(freqSet,Hmp1,supportData,br1,minConf)
        #判断合并后是否还会有后件元素，如果有，则继续合并，并计算新生成规则
        if(len(Hmp1)>1):
            rulesFromConseq(freqSet,Hmp1,supportData,br1,minConf)

注：如果你使用的时python3.x，需要对书中的代码进行调整，因为书中是基于python2.x编写的代码。

五、示例：发现国会投票中的模式

此示例中需要使用API获取数据，从https://github.com/votesmart/python-votesmart这个git地址上下载库压缩包，下载后解压，打开doc命令窗口进入解压目录中，如果你使用的是python2.x，直接使用语句python setup.py install 安装。
如果你使用的是python3.x需要先对压缩后目录中下图中的文件中的内容做相应改变，否则再使用命令行安装时会报错：

对目录中的这个文件进行一下更改：

安装好之后：要使用votesmartAPI,需要导入votesmart模块：

from votesmart import votesmart

接下来需要到 http://votesmart.org/services_api.php中注册以获得一个APIkey,这样才能使用该模块。

对数据进行解析以格式化

from time import sleep
from votesmart import votesmart
votesmart.apikey = 'a7fa40adec6f4a77178799fae4441030'
#votesmart.apikey = 'get your api key first'
def getActionIds():
    actionIdList = []; billTitleList = []
    fr = open('recent20bills.txt') 
    for line in fr.readlines():
        billNum = int(line.split('\t')[0])
        try:
            billDetail = votesmart.votes.getBill(billNum) #api call
            for action in billDetail.actions:
                if action.level == 'House' and \
                (action.stage == 'Passage' or action.stage == 'Amendment Vote'):
                    actionId = int(action.actionId)
                    print 'bill: %d has actionId: %d' % (billNum, actionId)
                    actionIdList.append(actionId)
                    billTitleList.append(line.strip().split('\t')[1])
        except:
            print "problem getting bill %d" % billNum
        sleep(1)                                      #delay to be polite
    return actionIdList, billTitleList

def getTransList(actionIdList, billTitleList): #this will return a list of lists containing ints
    itemMeaning = ['Republican', 'Democratic']#list of what each item stands for
    for billTitle in billTitleList:#fill up itemMeaning list
        itemMeaning.append('%s -- Nay' % billTitle)
        itemMeaning.append('%s -- Yea' % billTitle)
    transDict = {}#list of items in each transaction (politician) 
    voteCount = 2
    for actionId in actionIdList:
        sleep(3)
        print 'getting votes for actionId: %d' % actionId
        try:
            voteList = votesmart.votes.getBillActionVotes(actionId)
            for vote in voteList:
                if not transDict.has_key(vote.candidateName): 
                    transDict[vote.candidateName] = []
                    if vote.officeParties == 'Democratic':
                        transDict[vote.candidateName].append(1)
                    elif vote.officeParties == 'Republican':
                        transDict[vote.candidateName].append(0)
                if vote.action == 'Nay':
                    transDict[vote.candidateName].append(voteCount)
                elif vote.action == 'Yea':
                    transDict[vote.candidateName].append(voteCount + 1)
        except: 
            print "problem getting actionId: %d" % actionId
        voteCount += 2
    return transDict, itemMeaning

六、示例：发现毒蘑菇的相似特征

def readMushroom():
    return [line.split() for line in open('mushroom.dat').readlines()]

注：所有函数测试在main函数中进行，main函数如下：

if __name__ == "__main__":
    # dataSet = loadDataSet()
    # print("dataSet:",dataSet)
    # C1 = createC1(dataSet)
    # print("C1:",C1)
    # D = list(map(set,dataSet))
    # print("D:",D)
    # retList, supportData = scanD(D,C1,0.5)
    # print("L1:",retList)
    # print("supportData:",supportData)
    # L, supportData = apriori(dataSet)
    # # print("L:",L)
    # # print("supportData:",supportData)
    # # print(aprioriGen(L[0],2))
    # rules = generateRules(L,supportData,minConf=0.7)
    # print("rules:",rules)
    # dataSet = readMushroom()
    # L, supportData = apriori(dataSet,minSupport=0.3)
    # print("L:",L)
    # for item in L[1]:
    #     #求交集
    #     if item.intersection('2'):
    #         print("item:",item)
    # for item in L[3]:
    #     if item.intersection('2'):
    #         print("item:", item)
    #这里需要获得自己的key，才能使用API
    actionIdList, billTitleList = getActionIds()
    transDict, itemMeaning = getTransList(actionIdList,billTitleList)
    dataSet = [transDict[key] for key in transDict.keys()]
    L,suppData = apriori(dataSet,minSupport=0.5)

总结：Apriori算法从单元素项集开始，通过组合满足最小支持度要求的项集来形成更大的集合。每次增加频繁项集的大小，Apriori算法都会重新扫描整个数据集，当数据集很大时，这会降低频繁项集发现的速度。

Apriori算法相关参考：
https://blog.csdn.net/u010454729/article/details/49078505