约瑟夫问题

约瑟夫问题，也叫约瑟夫环。

问题描述： n（编号从0到n-1）个人围成一个圈，从0号人开始数（从1开始数），数到第m个人，这个人淘汰。又从下一个人开始，从1开始数，一直循环淘汰到只剩一人，这个人胜出。求这个人的编号。

解法一：模拟
这个问题很多人第一眼看到就觉得不是很简单吗，直接模拟就行啊。的确是，用一些列表类型的数据结构模拟一下就很容易做出来了。做法也因人而异。不过这方法只适用于人数和步数很小的时候，数量级一大就没办法了。模拟嘛，就是每m步去掉一个，一共要去掉n-1个，所以时间复杂度是O(nm)。这里我的方法不用傻乎乎的非要一步步的走，直接m步走，取余，就能得到要删除元素的下标。但是消耗时间还是没解法二快，也许是列表删除元素需要花费挺多时间，时间复杂度是O(n^2)。就算换成链表，也是耗时间，因为需要找对应下标才能删除，链表找下标也要很久。python代码如下。

# 模拟法
def josephus1(n: int, m: int) -> int:
    l = list(range(n))
    idx = 0
    for i in range(n - 1):
        idx = (idx + m - 1) % len(l)
        l.pop(idx)
    return l[0]

解法二：公式法
其实约瑟夫问题是有规律的。

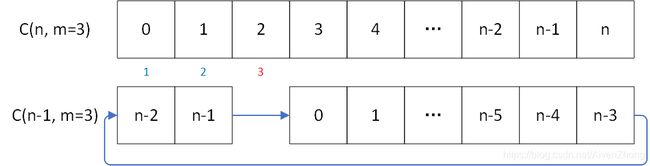
一个人数为n，步数为m的约瑟夫环（定义为C(n, m)），走了m步去掉这个人（编号为m % n - 1）之后，又从下一个人（编号为m）起，重新从0开始编号，这样就变成了另一个约瑟夫环C(n-1, m)。

然后一直走m步去掉一个，约瑟夫环就变成C(n-2, m)，C(n-3, m)…C(1, m)。所以求C(n, m)，就变成了求C(n-1, m)…求C(1, m)，求一个任务就等于求它的子任务。在这些不断的缩小的约瑟夫环中，都存在一个同样的人，就是幸存者，该编号在不同的约瑟夫环中是不同的。

还有一个规律，一个约瑟夫环元素编号可以被下一级约瑟夫环元素编号推出来。比如上图，我们把这一级的下标和下一级的下标进行对比。
3 — 0
4 — 1
5 — 2
…
n-2 — n-5
n-1 — n-4
n — n-3
0 — n-2
1 — n-1

可以发现，两个下标之间差了m=3步。子任务只要加上m（往左走）就等于原任务的下标了，严谨点还得取模。设原任务的下标为idx，子任务的下标为idx’，原任务的人数为n，则公式为：idx = ((idx’ + m) % n)。

通过这个公式就可以用子任务的下标推算出上一级任务的下标。而约瑟夫环C(1, m)中的幸存者明显就是0，这个幸存者是一直存在于上级的每个子任务中的，编号也不同。所以通过这个公式就可以一直推到C(n, m)中幸存者的标号。

比如求C(10, 3)
C(1, 3) = 0
C(2, 3) = (C(1, 3) + 3) % 2 = 1
C(3, 3) = (C(2, 3) + 3) % 3 = 1
…
C(10, 3) = (C(9, 3) + 3) % 3 = 3

python代码如下：

# 公式法
def josephus2(n: int, m: int) -> int:
    idx = 0
    for i in range(1, n + 1):
        idx = (idx + m) % i
    return idx


m = 3
for i in range(1, 11):
    print('C({}, {}) = {}'.format(i, m, josephus2(i, m)))

# C(1, 3) = 0
# C(2, 3) = 1
# C(3, 3) = 1
# C(4, 3) = 0
# C(5, 3) = 3
# C(6, 3) = 0
# C(7, 3) = 3
# C(8, 3) = 6
# C(9, 3) = 0
# C(10, 3) = 3

模拟图如下：