【Python学习笔记】2：收集最多价值奖品问题

收集最多价值奖品问题

题目描述：假设有一个6x6的棋盘，每个格子里有一个奖品(每个奖品的价值在100到1000之间)，现在要求从左上角开始到右下角结束，每次只能往右或往下走一个格子，所经过的格子里的奖品归自己所有。问最多能收集价值多少的奖品。

这是一个递推的问题，因为到达最后一个格子必须经过其上的格子或者其左的格子，所以到达这个格子最多能收集的奖品价值是左侧和上侧格子所能收集的奖品的最大价值(如果没有这个格子，就是0)中的较大者加上自身所在格子的奖品价值。而递推的入口在于到达[0][0]的奖品最大价值即为[0][0]本身的价值。有了递推表达式，也有了递推的入口，从而可以打表递推求解。

import random
List_vex=[[random.randint(100,1000) for i in range(6)] for j in range(6)] #生成随机的奖品图
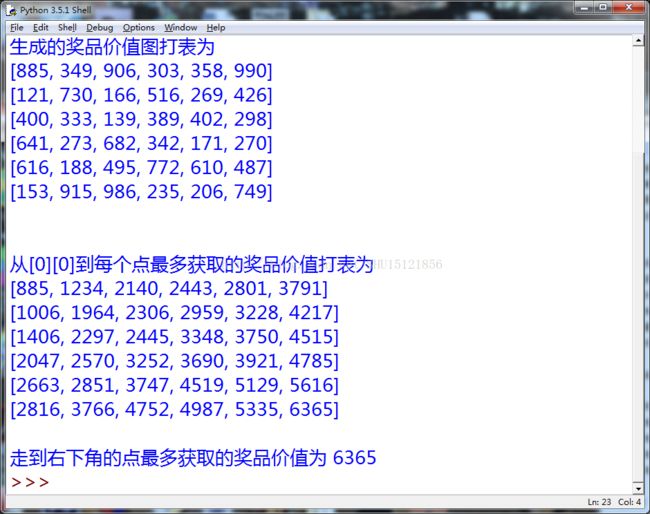
print("生成的奖品价值图打表为")
for i in range(6):
    print(List_vex[i]) #逐行输出看一下
print("\n")
List_maxpath=[[0 for i in range(6)] for j in range(6)] #这张图上的点表示到这点能获得的最大奖品值
for i in range(6):
    for j in range(6):
        List_maxpath[i][j]=max(List_maxpath[i-1][j] if i>0 else 0,List_maxpath[i][j-1] if j>0 else 0) + List_vex[i][j]
print("从[0][0]到每个点最多获取的奖品价值打表为")
for i in range(6):
    print(List_maxpath[i]) #逐行输出，矩阵最右下角的点值为所求
print("\n走到右下角的点最多获取的奖品价值为",List_maxpath[5][5])

运行结果：

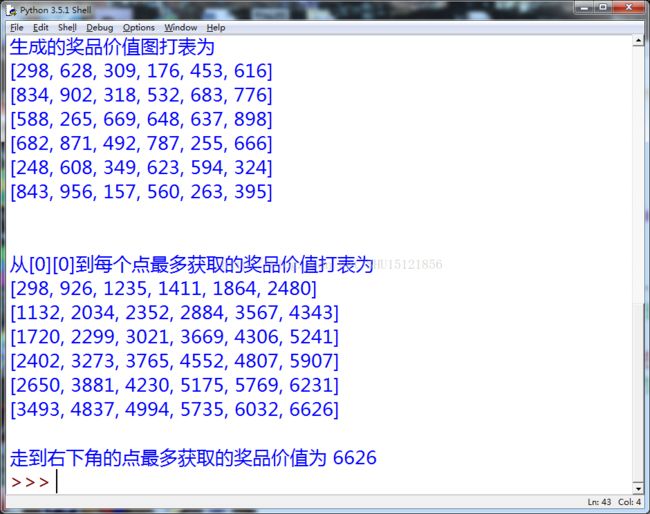
再运行一次：

random.randint(100,1000)用于随机生成100~1000之间的随机数，这里利用了列表推导式的方式将其用于生成列表的每一个元素。

List_maxpath[i-1][j] if i>0 else 0

相当于C/C++中的三目运算

i>0 ? List_maxpath[i-1][j] : 0

表示如果其上侧存在格子，就取到达那个格子的奖品最大价值数，否则取0，同样地对于其左侧的格子也是一样的道理。因为递推总是基于左侧和上侧的格子，因此循环也必须按照从左到右&从上到下(或者从上到下&从左到右)的顺序来进行。对每一步利用python内置的函数max()取了到达左侧和上侧格子的价值最大值，再与自身格子的奖品价值相加，完成一次递推。显然最终得到的点List_maxpath[5][5]即为所求。