一、简介
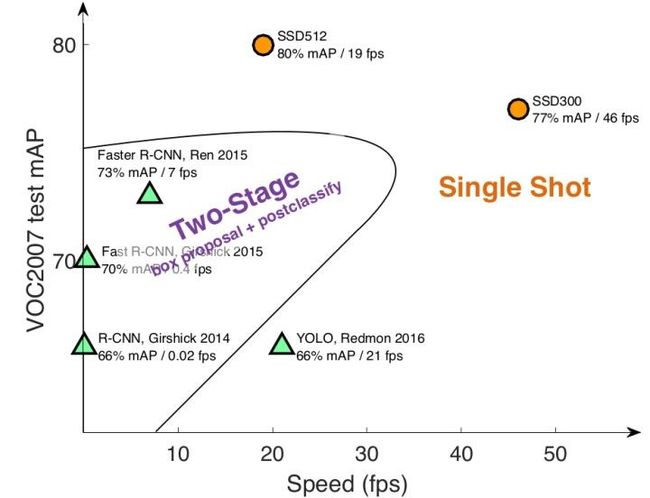
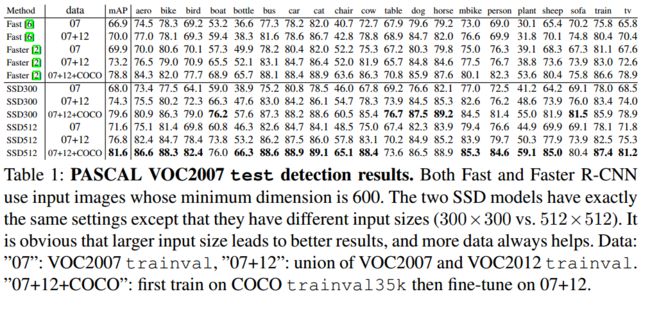
目标检测主流算法包括两个方面:(1)two-stage算法:如RCNN等系列算法,先通过启发式方法(selective search)或者CNN网络(RPN)产生一系列稀疏的候选框,然后对这些候选框进行分类与回归,two-stage方法的优势是准确度高;(2)one-stage算法:如Yolo和SSD,其主要思路是均匀地在图片的不同位置进行密集抽样,抽样时可以采用不同尺度和长宽比,然后利用CNN提取特征后直接进行分类与回归,整个过程只需要一步,所以其优势是速度快,,但是均匀的密集采样的一个重要缺点是训练比较困难,这主要是因为正样本与负样本(背景)极其不均衡,,导致模型准确度稍低。图为几种主流算法的对比:
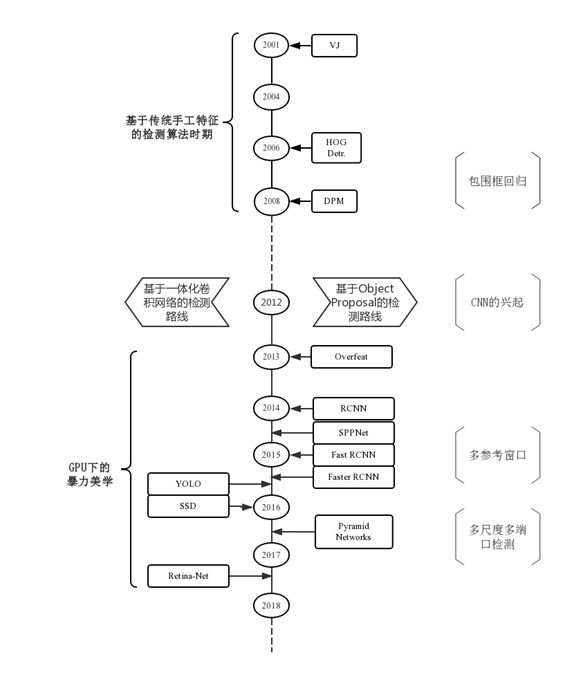
以及目标检测算法发展的流程图:
二、参考文献
Liu W , Anguelov D , Erhan D , et al. SSD: Single Shot MultiBox Detector[J]. 2015.
https://arxiv.org/pdf/1512.02325.pdf
Redmon J , Divvala S , Girshick R , et al. You Only Look Once: Unified, Real-Time Object Detection[J]. 2015.
https://arxiv.org/pdf/1506.02640.pdf
DSSD : Deconvolutional Single Shot Detector
https://arxiv.org/pdf/1701.06659.pdf
Enhancement of SSD by concatenating feature maps for object detection
https://arxiv.org/pdf/1705.09587.pdf
Focal Loss for Dense Object Detection
https://arxiv.org/pdf/1708.02002.pdf
博客:
- 目标检测算法之SSDhttps://blog.csdn.net/xiaohu2022/article/details/79833786
三、算法详解
1.模型
(1)多尺度特征图检测
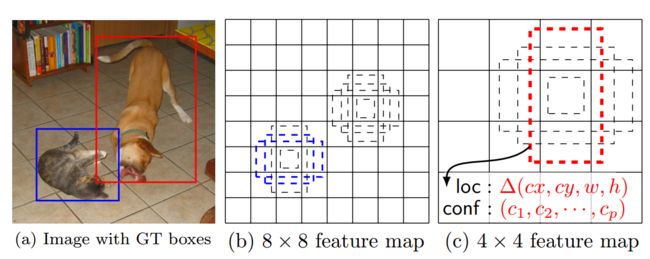
CNN网络一般前面的特征图比较大,后面会逐渐采用卷积或者池化来降低特征图大小,这下图所示:
一个8×8和一个4×4的特征图,它们都用来做检测。较大的特征图来用来检测相对较小的目标,而较小的特征图负责检测大目标。
(2)使用卷积进行检测
与Yolo最后采用全连接层不同,SSD直接采用卷积对不同的特征图来进行提取检测结果。对于形状为m×n×p的特征图,只需要采用3×3×p这样比较小的卷积核得到检测值。同时借鉴了DeepLab-LargeFOV的思想,分别将VGG16的全连接层fc6和fc7转换成3×3卷积层conv6和1×1卷积层conv7,为了配合这种变化,使用了空洞卷积。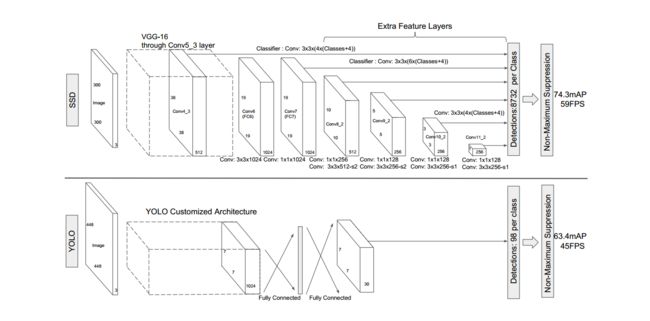
(3)先验框(default boxes)
在Yolo中,每个单元预测多个边界框,但是其都是相对这个单元本身(正方块),但是真实目标的形状是多变的,Yolo需要在训练过程中自适应目标的形状。而SSD借鉴了Faster R-CNN中anchor的理念,每个单元设置尺度或者长宽比不同的先验框,预测的边界框(bounding boxes)是以这些先验框为基准的,在一定程度上减少训练难度。
对于每个grid的每个default box,都会输出一列独立的检测值,包括各个类别的置信度/评分以及边界框(cx,cy,w,h)即中心坐标和宽高。类似Faster R-CNN,SSD算法回归offsets(坐标的偏置值)
先验框位置用\(d=(d^{cx},d^{cy},d^w,d^h)\)表示,其对应边界框用\(b=(b^{cx},b^{cy},b^w,b^h)\)表示,那么边界框的预测值l其实是b相对于d的转换值:
\[ \begin{array}{l}l^{cx}=(b^{cx}-d^{cx})/d^w,l^{cy}=(b^{cy}-d^{cy})/d^h\\l^w\;=\;\log\left(b^w/d^w\right),l^h\;=\;\log\left(b^h/d^h\right)\end{array} \]
预测时要反向这个过程。
2.训练
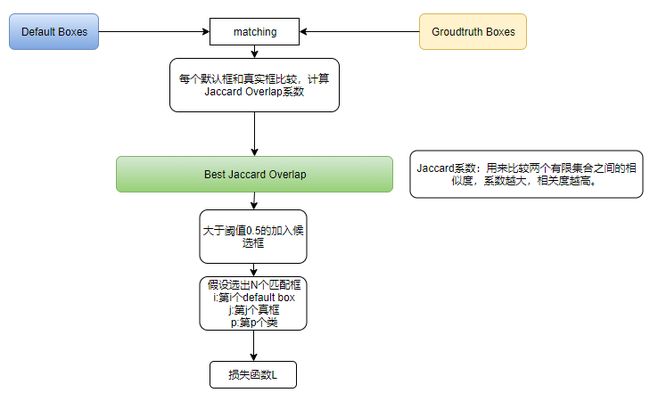
(1)匹配策略
在训练时,需要建立真值框与先验框之间的一一对应关系。最初,该算法是将与真值框之间jaccard overlap系数最高的default box与真值框匹配起来,这样就是一一对应的关系。但是一个图片中ground truth是非常少的, 而先验框却很多,如果仅按此原则匹配,很多先验框会是负样本,正负样本极其不平衡。因此,最终该算法将jaccard overlap系数高于0.5的真值框和先验框匹配起来。
(2)损失函数
\[ L_{conf}(x,c,l,g)=\frac1N(L_{conf}(x,c)+\alpha L_{loc}(x,l,g) \]
N:匹配的默认框的数量,如果N=0,则L=0
L~conf~:在多种类别置信度上的softmax损失
L~loc~:预测框和真值框参数之间的平滑L1损失
i:第i个先验框
j:第j个真框
p:第p个类
x: x~i,j~^p^={0,1},当x~i,j~^p^=1时表示第i个先验框与第j个真值框匹配
c:置信度(confidence)
l:预测框
g:真值框
(3)先验框生成
不同特征图设置的先验框数目不同。先验框的设置,包括尺度(或者说大小)和长宽比两个方面。对于先验框的尺度,其遵守一个线性递增规则:随着特征图降低,先验框尺度线性增加:
\[ s_k=s_{min}+\frac{s_{max}-s_{min}}{m-1}(k-1),\;k\in\lbrack1,m\rbrack \]
其中m指的特征图个数,但却是5,因为第一层(Conv4_3层)是单独设置的,s~k~表示先验框大小相对于图片的比例,而s~min~和s~max~表示比例的最小值与最大值,paper里面取0.2和0.9。
对于长宽比,\(w_k^a=s_k\sqrt[]{a_r}\),\(a_r\in\{1,2,3,\frac12,\frac13\}\)(这里\(w_k^a\)为实际的尺度大小而不是比例)。特别的对于\(a_r=1\)且尺度为\(s_k\)的先验框,还会设置一个尺度为\(s_k^‘=\sqrt{s_ks_{k+1}}\)的先验框。但具体实现比一定是6个先验框。结合上述网络结构图,可以计算出图片每次通过网络都会生成8732个先验框。
\[ 38\times38\times4+19\times19\times6+10\times10\times6+5\times5\times6+3\times3\times4+1\times1\times4=8732 \]
(4)难例挖掘
在步骤(1)匹配过后,还是会有很多先验框为负样本,正负样本存在显著的不平衡。我们不使用所有的负样本,而是用每个负样本的最高置信度对它们进行排序,选择top-k个,使得负样本和正样本的比率为3:1。这样可以带来更快的优化和更稳定的训练。
(5)数据增广
(6)算法性能
Fast R-CNN和Faster R-CNN与SSD算法对比:
多尺度输出层
四、待改进
- 因为在SSD中,不同层的feature map都是独立作为分类网络的输入,因此容易出现相同物体被不同大小的框同时检测出来。
- 对小物体的检测效果较差。
- 难例挖掘
R-SSD
Enhancement of SSD by concatenating feature maps for object detection
主要解决1,2
D-SSD
DSSD : Deconvolutional Single Shot Detector
主要解决2
Focal Loss
首先看交叉熵损失
\[ cross\_entropy(p,y)=\left\{\begin{array}{lc}-\log\left(p\right)&if\;y=1\\-\log\left(1-p\right)&else\end{array}\right. \]
令\(\begin{array}{l}p_t=\left\{\begin{array}{lc}p&if\;y=1\\1-p&else\end{array}\right.\\\end{array}\),则重写交叉熵损失函数:
\[ \begin{array}{l}cross\_entropy(p,y)=cross\_entropy(p_t)=-\log\left(p_t\right)\\\end{array} \]
但是由于正负样本不均,故最初,作者起初只是在损失函数前增加了一个控制权重,如下所示:
\[ \begin{array}{l}cross\_entropy(p_t)=-\alpha\log\left(p_t\right)\\\end{array} \]
后来,为了区分易分和难分样本,作者给出的最终的focal loss表达式:
\[ focal\_loss=-\alpha(1-p_t)^\gamma\log\left(p_t\right) \]
从上式中可以看出,样本越易分,则\(p_t\)值越大,那么其loss就越小;反之,对于难分样本,其loss就更大。通过试验,\(\alpha=0.25\)和\(\gamma=2\)效果最好。