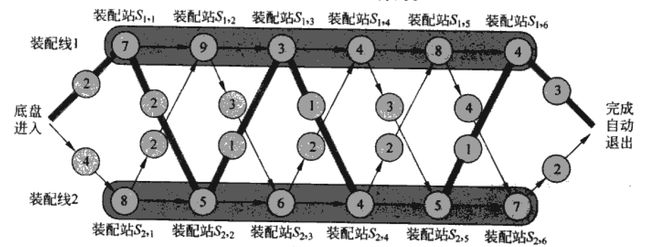
已算法导论图示为例
两条生产线上,产品经过各个装配工作位直到加工完成所耗费的时间都标记出来了,同一生产线的装配工作位转移不花费时间。
试图求出最快流程。
动态规划是利用最优子结构自底向上求解。
也就是说要求出最后完成的最快流程(Si,6)我们需要先知道Si,5工位的最快流程,
而直到Si,5工位的最快流程就需要知道Si,4工位的最快流程 直到求出Si,1的最快流程
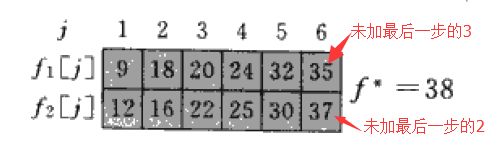
s1,1最优解是2+7
s2,2最优解是4+8
s1,2最优解是s1,1+9 = 18
s2,2最优解是s1,1+2+5=16
s1,3最优解是s2,2+1+3=20
s2,3最优解是s2,2+6=22
......
s1,6最优解是s2,5+1+4+3=38
s2,6最优解是s2,5+7+2=39
算法请查看算法导论第二版194页
//==============================================
贪婪算法 则是自顶向下 不考虑子问题解法只选择当前最优选择
那么过程如下
s1,1耗费是2+7=9
s2,2耗费是4+8=12
第一步选择s1,1
.......
最后得出
s1,1->s2,2->s1,3->s1,4->s1,5(s2,5)->s1,6
倒数第二步有两个选择 因为s1,4->s1,5 == s1,4->s2,5 == 8
最后贪婪算法得出的最优流程耗费为39 或者40
代码后继增加.....