论文学习笔记：CenterNet（Object as Points）
前言
CenterNet摒弃了以往主流的anchor-base的思路,利用关键点估计的方法找到图像中目标的中心点,并回归出框的尺寸等其他属性,以此确定出目标所在的位置和类别.不需要非极大值抑制NMS的后处理,能够端到端训练.相比于CornerNet、CenterNet-Triplets等其他anchor-free的算法,不需要关键点配对的步骤,节省了计算资源.在MS COCO数据集实现了SOTA的精度，尤其是与YOLOv3作比较，在相同速度的条件下，CenterNet的精度比YOLOv3提高了4个左右的点,同时也做到了实时性.当然,论文中还扩展到了人体姿态检测、3D bbox识别等领域,适用性很强.
论文传送带：https://arxiv.org/pdf/1904.07850
代码传送带：https://github.com/xingyizhou/CenterNet
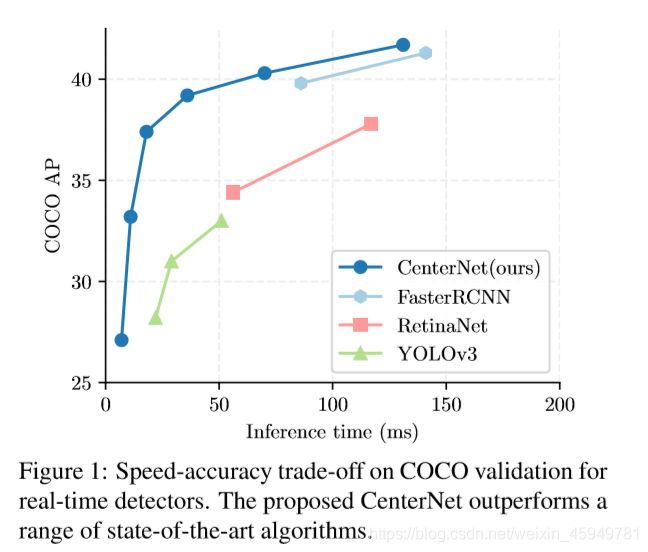
网络理论分析
首先假设输入图像为 I ∈ R W × H × 3 I \in R^{W \times H \times 3} I∈RW×H×3，其中 W W W 和 H H H 分别为图像的宽和高.网络的目标是预测生成关键点的热点图： Y ^ = [ 0 , 1 ] W R × H R × C \hat{Y}=[0,1]^{\frac{W}{R}\times\frac{H}{R}\times C} Y^=[0,1]RW×RH×C,其中 其中 R R R是输出热图的缩小倍数,论文中 R R R为4，而 C C C是关键点类别数,如在COCO目标检测任务中为80，代表当前有80个类别. Y x , y , c ^ \hat{Y_{x,y,c}} Yx,y,c^的含义就是检测到物体的预测值， Y x , y , c ^ = 1 \hat{Y_{x,y,c}}=1 Yx,y,c^=1表示对于类别 C C C，在当前 (x,y) 坐标中检测到了这种类别的物体，而 Y x , y , c ^ = 0 \hat{Y_{x,y,c}}=0 Yx,y,c^=0 则表示当前当前这个坐标点不存在类别为 c 的物体.
接下来从训练阶段和推理阶段去分析网络的原理。
训练阶段
训练阶段的话，需要做的第一步工作就是计算得到关键点的真实标签 Y，然后进行训练，利用监督学习的方式去学习参数权重。
对于每个标签图(ground truth)中的某一 C C C类，我们要将真实关键点计算出来用于训练，中心点的计算方式为 p = ( x 1 + x 2 2 , y 1 + y 2 2 ) p=(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}) p=(2x1+x2,2y1+y2)，对于下采样后的坐标，我们设为 p ^ = [ p R ] \hat{p}=[\frac{p}{R}] p^=[Rp] ，其中 R R R 是上文中提到的下采样因子4。所以我们最终计算出来的中心点是对应低分辨率的中心点。然后我们利用 Y = [ 0 , 1 ] W R × H R × C Y=[0,1]^{\frac{W}{R}\times\frac{H}{R}\times C} Y=[0,1]RW×RH×C来对图像进行标记，在下采样的[128,128]图像中将ground truth point以 Y = [ 0 , 1 ] W R × H R × C Y=[0,1]^{\frac{W}{R}\times\frac{H}{R}\times C} Y=[0,1]RW×RH×C 的形式，用一个高斯核
来将关键点分布到特征图上，其中 σ p \sigma_p σp 是一个与目标大小(也就是w和h)相关的标准差。如果某一个类的两个高斯分布发生了重叠，直接取元素间最大的就可以。每个点 Y = [ 0 , 1 ] W R × H R × C Y=[0,1]^{\frac{W}{R}\times\frac{H}{R}\times C} Y=[0,1]RW×RH×C 的范围是0-1,而1则代表这个目标的中心点，也就是我们要预测要学习的点。
预测中心关键点的损失函数采用了Focal loss 的变形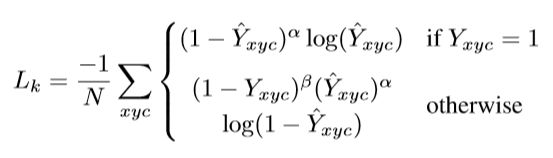
其中 α \alpha α和 β \beta β是Focal Loss的超参数，论文中取2和4. N N N是图像 I I I 的的关键点数量，用于将所有的positive focal loss标准化为1。对于容易检测的中心点，适当减少其训练比重也就是loss值，当 Y = 1 Y=1 Y=1 的时候， ( 1 − Y x y c ^ ) α (1-\hat{Y_{xyc}})^\alpha (1−Yxyc^)α 就充当了矫正的作用，假如 Y ^ \hat{Y} Y^ 接近1的话，说明这个是一个比较容易检测出来的点，那么 ( 1 − Y x y c ^ ) α (1-\hat{Y_{xyc}})^\alpha (1−Yxyc^)α 就相应比较低了。而当 Y ^ \hat{Y} Y^ 接近0的时候，说明这个中心点还没有学习到，所以要加大其训练的比重，因此 ( 1 − Y ^ ) α (1-\hat{Y})^\alpha (1−Y^)α就会很大。
当 otherwise 的时候，这里对实际中心点的其他近邻点的训练比重(loss)也进行了调整.此时otherwise 的时候预测值 Y x y c ^ α \hat{Y_{xyc}}^\alpha Yxyc^α理应是0，如果不为0的且越来越接近1的话， Y x y c ^ α \hat{Y_{xyc}}^\alpha Yxyc^α的值就会变大从而使这个损失的训练比重也加大；而 ( 1 − Y x y c ) β (1-{Y_{xyc}})^\beta (1−Yxyc)β 则对中心点周围的和中心点靠得越近的点也做出了调整(因为与实际中心点靠的越近的点可能会影响干扰到实际中心点，造成误检测)，因为 Y x y c Y_{xyc} Yxyc在上文中已经提到，是一个高斯核生成的中心点，在中心点周围扩散,由1慢慢变小但是并不是直接为0.因此与中心点距离越近， Y x y c Y_{xyc} Yxyc越接近1， ( 1 − Y x y c ) β (1-{Y_{xyc}})^\beta (1−Yxyc)β 越小，相反则越大.
那么 ( 1 − Y x y c ) β (1-{Y_{xyc}})^\beta (1−Yxyc)β 和 Y x y c ^ α \hat{Y_{xyc}}^\alpha Yxyc^α是怎么协同工作的呢？对于距离实际中心点近的点， Y x y c Y_{xyc} Yxyc值接近1，但是预测出来这个点的值 Y x y c ^ \hat{Y_{xyc}} Yxyc^比较接近1，这个显然是不对的，它应该检测到为0，因此用 Y x y c ^ α \hat{Y_{xyc}}^\alpha Yxyc^α惩罚一下，使其LOSS比重加大些；但是因为这个检测到的点距离实际的中心点很近了，检测到的 Y x y c ^ \hat{Y_{xyc}} Yxyc^接近1也情有可原，那么我们就同情一下，用 ( 1 − Y x y c ) β (1-{Y_{xyc}})^\beta (1−Yxyc)β 来安慰下，使其LOSS比重减少些。对于距离实际中心点远的点， Y x y c Y_{xyc} Yxyc值接近0，如果预测出来这个点的值 Y x y c ^ \hat{Y_{xyc}} Yxyc^比较接近1，肯定不对，需要用 Y x y c ^ α \hat{Y_{xyc}}^\alpha Yxyc^α惩罚，如果预测出来的接近0，那么差不多了，拿 Y x y c ^ α \hat{Y_{xyc}}^\alpha Yxyc^α来安慰下，使其损失比重小一点；至于 ( 1 − Y x y c ) β (1-{Y_{xyc}})^\beta (1−Yxyc)β的话，因为此时预测距离中心点较远的点，所以这一项使距离中心点越远的点的损失比重占的越大，而越近的点损失比重则越小，这相当于弱化了实际中心点周围的其他负样本的损失比重，相当于处理正负样本的不平衡了。结合上面两种情况, ( 1 − Y x y c ) β (1-{Y_{xyc}})^\beta (1−Yxyc)β 和 Y x y c ^ α \hat{Y_{xyc}}^\alpha Yxyc^α来限制easy example导致的gradient被easy example dominant的问题，而 ( 1 − Y x y c ) β (1-{Y_{xyc}})^\beta (1−Yxyc)β 则用来处理正负样本的不平衡问题(因为每一个物体只有一个实际中心点，其余的都是负样本，但是负样本相较于一个中心点显得有很多)。
同时增加了对于每个关键中心点的局部偏移量的预测和修正,所有类别共享相同的偏移预测,采用损失函数训练.
得到关键点的估计之后,还需要预测其他目标属性.假设目标 k k k的bbox的坐标为 ( x 1 ( k ) , y 1 ( k ) , x 2 ( k ) , y 2 ( k ) ) (x_1^{(k)},y_1^{(k)},x_2^{(k)},y_2^{(k)}) (x1(k),y1(k),x2(k),y2(k)),类别是 c k c_k ck,中心点为 p k = ( x 1 k + x 2 k 2 , y 1 k + y 2 k 2 ) p_k=(\frac{{x_1^{k}}+{x_2^{k}}}{2},\frac{{y_1^{k}}+{y_2^{k}}}{2}) pk=(2x1k+x2k,2y1k+y2k),；利用关键点估计预测 Y ^ \hat{Y} Y^预测所有的中心关键点，然后对每个目标的 s i z e size size进行回归，得到 s k = ( x 2 k − x 1 k , y 2 k − y 1 k ) s_k=(x_2^{k}-x_1^{k},y_2^{k}-y_1^{k}) sk=(x2k−x1k,y2k−y1k).对所有目标类使用 L 1 L_1 L1损失函数 L s i z e L_{size} Lsize去训练进行单尺寸预测 .
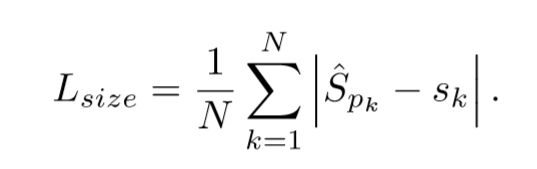因此整体的损失函数为
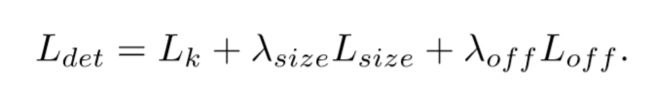总的来说,整个CenterNet网络的推理主要通过生成热力图上的前n个峰值点预测关键估计点 ,每个位置有(C+4)个输出,根据偏移量 和尺寸 得到目标的类别和bbox,无需NMS后处理.
推理阶段
在预测阶段，首先针对一张图像进行下采样，随后对下采样后的图像进行预测，对于每个类在下采样的特征图中预测中心点，然后将输出图中的每个类的热点单独地提取出来。具体怎么提取呢？就是检测当前热点的值是否比周围的八个近邻点(八方位)都大(或者等于)，然后取100个这样的点，采用的方式是一个3x3的MaxPool，类似于anchor-based检测中nms的效果。
代表 C k C_k Ck 类中检测到的一个点。每个关键点的位置用整型坐标 ( x i , y i ) (x_i,y_i) (xi,yi)表示 ，然后使用 Y x y c ^ \hat{Y_{xyc}} Yxyc^表示当前点的confidence，随后使用坐标来产生标定框：
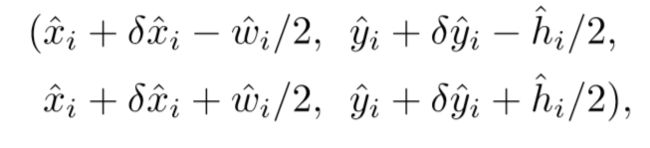
最终是根据模型预测出来的 Y ^ = [ 0 , 1 ] W R × H R × C \hat{Y}=[0,1]^{\frac{W}{R}\times\frac{H}{R}\times C} Y^=[0,1]RW×RH×C 值，也就是当前中心点存在物体的概率值，代码中设置的阈值为0.3，也就是从上面选出的100个结果中调出大于该阈值的中心点作为最终的结果。
不足
CenterNet的缺点也是有的，在实际训练中，如果在图像中，同一个类别中的某些物体的GT中心点，在下采样时会挤到一块，也就是两个物体在GT中的中心点重叠了，CenterNet对于这种情况也是无能为力的，也就是将这两个物体的当成一个物体来训练(因为只有一个中心点)。同理，在预测过程中，如果两个同类的物体在下采样后的中心点也重叠了，那么CenterNet也是只能检测出一个中心点。有一个需要注意的点，CenterNet在训练过程中，如果同一个类的不同物体的高斯分布点互相有重叠，那么则在重叠的范围内选取较大的高斯点。