快速排序基本思想及代码实现-史上最通俗易懂的

1、算法思想
    　快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略，通常称其为分治法(Divide-and-ConquerMethod)。
（1） 分治法的基本思想
    　分治法的基本思想是：将原问题分解为若干个规模更小但结构与原问题相似的子问题。递归地解这些子问题，然后将这些子问题的解组合为原问题的解。

（2）快速排序的基本思想
    　设当前待排序的无序区为R[low..high]，利用分治法可将快速排序的基本思想描述为：
①分解： 
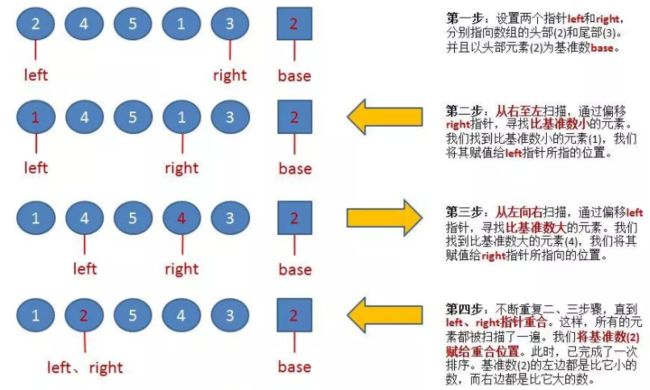
    　在R[low..high]中任选一个记录作为基准(Pivot)，以此基准将当前无序区划分为左、右两个较小的子区间R[low..pivotpos-1)和R[pivotpos+1..high]，并使左边子区间中所有记录的关键字均小于等于基准记录(不妨记为pivot)的关键字pivot.key，右边的子区间中所有记录的关键字均大于等于pivot.key，而基准记录pivot则位于正确的位置(pivotpos)上，它无须参加后续的排序。
  注意：
    　划分的关键是要求出基准记录所在的位置pivotpos。划分的结果可以简单地表示为(注意pivot=R[pivotpos])：
    　R[low..pivotpos-1].keys≤R[pivotpos].key≤R[pivotpos+1..high].keys
                  其中low≤pivotpos≤high。
②求解： 
   　 通过递归调用快速排序对左、右子区间R[low..pivotpos-1]和R[pivotpos+1..high]快速排序。

③组合： 
    　因为当"求解"步骤中的两个递归调用结束时，其左、右两个子区间已有序。对快速排序而言，"组合"步骤无须做什么，可看作是空操作。

2、快速排序算法QuickSort
  void QuickSort(SeqList R，int low，int high)
   { //对R[low..high]快速排序
     int pivotpos； //划分后的基准记录的位置
     if(low        pivotpos=Partition(R，low，high)； //对R[low..high]做划分
        QuickSort(R，low，pivotpos-1)； //对左区间递归排序
        QuickSort(R，pivotpos+1，high)； //对右区间递归排序
      }
    } //QuickSort

#include 
int a[101],n;//定义全局变量，这两个变量需要在子函数中使用
void quicksort(int left, int right) {
	int i, j, t, temp;
	if(left > right)
		return;
    temp = a[left]; //temp中存的就是基准数
    i = left;
    j = right;
    while(i != j) { //顺序很重要，要先从右边开始找
    	while(a[j] >= temp && i < j)
    		j--;
    	while(a[i] <= temp && i < j)//再找右边的
    		i++;       
    	if(i < j)//交换两个数在数组中的位置
    	{
    		t = a[i];
    		a[i] = a[j];
    		a[j] = t;
    	}
    }
    //最终将基准数归位
    a[left] = a[i];
    a[i] = temp;
    quicksort(left, i-1);//继续处理左边的，这里是一个递归的过程
    quicksort(i+1, right);//继续处理右边的 ，这里是一个递归的过程
}
int main() {
	int i;
    //读入数据
	scanf("%d", &n);
	for(i = 1; i <= n; i++)
		scanf("%d", &a[i]);
    quicksort(1, n); //快速排序调用
    //输出排序后的结果
    for(i = 1; i < n; i++)
    	printf("%d ", a[i]);
    printf("%d\n", a[n]);
    return 0;
}

我在这里发明了一种简单的，通俗易懂的快速排序方法，代码如下：

#include 

void swap(int a[],int i,int j)
{
	int t;
	t=a[i];
	a[i]=a[j];
	a[j]=t;
}

void quickSort(int a[],int left,int right)
{
	int mid,i,j;

	if(left>=right)
		return;

	mid = a[left];
	i=left;
	j=left+1;
	while(j<=right)
	{
		if(a[j]<=mid)
		{
			i++;
			swap(a,i,j);
		}
		j++;
	}
	swap(a,i,left);
	quickSort(a,left,i-1);
	quickSort(a,i+1,right);
}

int main()
{
	int a[9]={8,2,6,12,1,9,5,5,10};
	int i;
	quickSort(a,0,8);/*排好序的结果*/
	for(i=0;i<9;i++)
	printf("%d\n",a[i]);
	return 0;
}

核心代码在这里：

观察上面代码可知，j一直在向后移，而i只有在发生交换操作后才后移。可见，小于等于i坐标的数值都是小于等于mid值的，大于i坐标的数值都是大于mid值的。

i是先加1再交换的。

简单吧，通俗易懂吧，哈哈，希望对大家有帮助！

来源：我是码农，转载请保留出处和链接！

本文链接：http://www.54manong.com/?id=1236

'); (window.slotbydup = window.slotbydup || []).push({ id: "u3646208", container: s }); })();

'); (window.slotbydup = window.slotbydup || []).push({ id: "u3646147", container: s }); })();