图的拓扑排序的算法实现，C语言，栈，超详细版本

数据结构课程设计 设计说明书 图的拓扑排序的算法实现

设计内容：

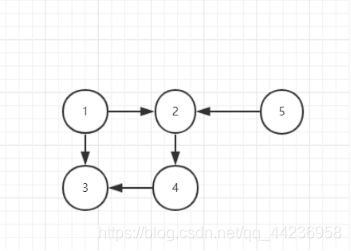
拓扑排序在工程管理领域中的应用广泛，可用于判断工程能否顺利开展，即判断有向图中是否存在回路。对于一个有向图，先由键盘输入其顶点和弧的信息，采用恰当存储结构保存该有向图后，依据拓扑排序算法思想输出其相应的顶点拓扑有序序列，并提示用户是否存在回路。

设计要求：

1）问题分析和任务定义：根据设计题目的要求，充分地分析和理解问题，明确问题要求做什么？
2）逻辑设计：写出抽象数据类型的定义，各个主要模块的算法，并画出模块之间的调用关系图。
3）详细设计：定义相应的存储结构并写出各函数的伪码算法。
4）程序编码：把详细设计的结果进一步求精为程序设计语言程序。
5）程序调试与测试：采用自底向上，分模块进行，即先调试低层函数。
6）结果分析：程序运行结果包括正确的输入及其输出结果和含有错误的输入及其输出结果。算法的时间、空间复杂性分析。
7）编写课程设计报告。

设计了一个图的拓扑排序，判断有向图中是否存在回路，按照规则输入，并输出相应的顶点拓扑有序序列，并提示用户是否存在回路，采用DEV.C++作为软件开发环境，采用邻接表来存储图中的各条边的关系，并用拓扑排序算法思想排序和栈的思想将其输出
关键词：拓扑排序；邻接表；栈

1.课题描述

拓扑排序针对的对象是一个有向无环图，将图中的节点排成一个线性序列，这就是拓扑排序。线性序列要求满足，图中任意一对节点u,v若存在有向边，则u必然是在v的前面。满足这个条件的序列，叫拓扑序列，得到这个拓扑序列的过程叫做拓扑排序。
假如要完全一个工程项目，该项目分为很多个小步骤，这些小步骤之间有先后依赖的关系，也就是说有些任务是只能先完成A，然后才能继续完成B。最终只有这些小目标都完成了，才能够达成最终的目标。这个时候，可以对这些任务，建立一个有向图，节点表示任务，有向边表示任务的先后关系。这个有向图有个官方名字，叫顶点活动图（AOV网），顶点表示活动，边表示活动时间的先后关系。

2需求分析

(1)输入的形式
首先是输入要排序的顶点数和弧数，都为整型;再输入各顶点的值，为正型;然后输入各条弧的两个顶点值，先输入弧头，再输入弧尾，中间用分隔符隔开。
(2)输出的形式
首先输出建立的邻接表，然后是最终各顶点的出度数，再是拓扑排序的序
列，并且每输出一个顶点，就会输出一次各顶点的入度数。
(3)程序所能达到的功能
因为该程序是求拓扑排序，所以算法的功能就是要输出拓扑排序的序列，在一个有向图无环图中，输出的拓扑序列就表示各顶点间的关系；若为有环图，则提示错误，无排序序列。

3概要设计

3.1抽象数据类型

（1）图

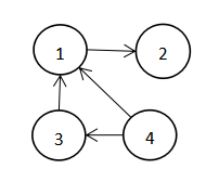
图(Graph)是由顶点的有穷非空集合和顶点直接边的集合组成,通常表示为G(V,E)，其中G表示一个图,V是图G中顶点的集合,E是图G中的边的集合。图中的数据元素，我们称为顶点；图不存集，图中不允许没有顶点任何两个顶点之间都可能有关系,顶点之间的逻辑关系用边表示,如图3.1所示:

图3.1 有向图G1

ADT Graph{  
      数据对象V：
     V是具有相同特性的数据元素的集合，称为顶点集。  
     数据关系R：R={VR}  
     VR={<v,w>|v,w∈V且P(v,w)，<v,w>表示从v到w的弧，  
     谓词P(v,w)定义了弧<v,w>的意义或信息}  
     基本操作：  
CreateGraph( &G, V, VR )  
     初始条件：V是图的顶点集，VR是图中弧的集合。  
     操作结果：按V和VR的定义构造图G。    
LocateVex( G, u )  
     初始条件：图G存在，u和G中顶点有相同特征。  
     操作结果：若G中存在顶点u，则返回该顶点在图中位置；否则返回其它息。  
GetVex( G, v )  
     初始条件：图G存在，v是G中某个顶点。  
     操作结果：返回v的值。  
FirstAdjVex( G, v )  
 初始条件：图G存在，v是G中某个顶点。  
     操作结果：返回v的第一个邻接顶点。若顶点在G中没有邻接顶点，则返“空”。  
}ADT Graph 

（2）栈

拓扑排序在实现时，还需建立一个存放入度为0的顶点的栈。

栈（stack）又名堆栈，它是一种限定在表尾进行插入或删除操作的线性表。表尾被称为栈顶，相对地，把另一端称为栈底。
不含元素的空表称为空栈。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。
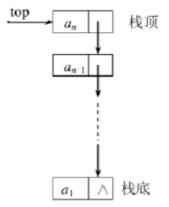
假设栈S=(a1,a2,…,a3)S=(a1,a2,…,a3),则称a1a1为栈底元素，anan为栈顶元素。栈中元素按a1,a2,…,ana1,a2,…,an的次序进栈，退栈的第一个元素应该为栈顶元素。换句话说，栈的修改是按后进先出的原则进行的，如图3.2所示:

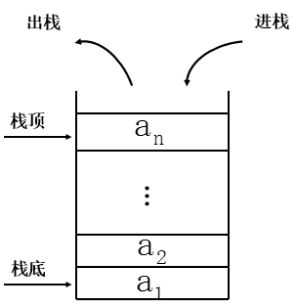
图3.2 栈的示意图

ADT Stack {
    数据对象：D＝{ai| ai∈ElemSet, i=1,2,...,n, n≥0 }
    数据关系：R1＝{ <ai-1,ai>| ,ai-1,ai∈D, i=2,...,n }
    约定an端为栈顶，a1端为栈底。
基本操作：
StackNode(&S) 
    操作结果：构造一个空栈 S。 
Push(&S, e)
    初始条件：栈 S 已存在。
    操作结果：插入元素 e 为新的栈顶元素。
Pop(&S, &e)
    初始条件：栈 S 已存在且非空。
    操作结果：删除 S 的栈顶元素，并用 e 返回其值。
}

3.2程序所含模块

（1）主程序模块，定义变量
（2）建立有向图模块CreateUDG()
（3）建立顶点在图定位模块LocateVex()
（3）建立拓扑排序算法模块TopologicalSort()
（4）建立入栈模块Push()
（5）建立出栈模块Pop()

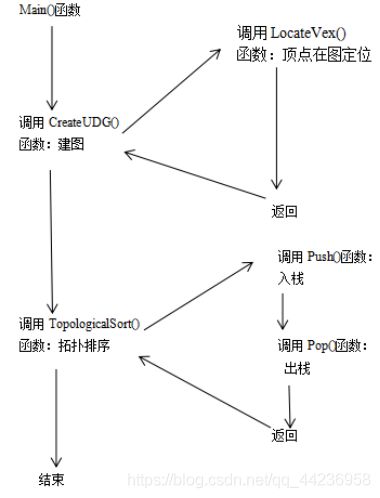
3.3程序的调用关系

程序的调用关系如图所示：

图3.3 函数调用关系图

4详细设计

4.1储存结构的实现

（1）图储存结构

有向图：用邻接实现有向图，图中每个顶点vi的所有邻接点构成一个线性表，由于邻接点的个数不定，所以用单链表存储，无向图称为顶点vi的边表，有向图则称为以vi为弧尾的出边表。顶点表的各个结点由data和firstedge两个域表示，data是数据域，存储顶点的信息。
firstedge是指针域，指向边表的第一个结点，即此顶点的第一个邻接点。边表结点由adjvex和next两个域组成。adjvex是邻接点域，存储某顶点的邻接点在顶点表中的下标，next则存储指向边表中下一个结点的指针。如图4.1及图4.2所示：

图4.1 顶节点和边界点的结构

图4.2 邻接表储存有向图

图的邻接表储存表示：

typedef struct ArcNode{    //链表结点
	int adjvex;           //邻接表创建无向网的实现
	ArcNode *nextarc;    //指向下一条边的指针
	OtherInfo info;       //和边相关的信息
}ArcNode;
 
typedef struct VNode{   //头结点
	VerTexType data;   //顶点信息
	ArcNode *firstarc;//指向第一条依附该顶点的边的指针
}VNode,AdjList[MVNum];//AdjList 表示邻接表类型
 
typedef struct{
	AdjList vertices;     //邻接表头结点数组
	int vexnum, arcnum;   //图的顶点数和弧数
}ALGraph;

（2）栈的储存结构

用链式存储结构存储的栈称为链栈，链栈通常用单链表来表示。它的结点结构与单链表的结构一样，都是由数据域data和引用域next两部分组成。

图 4.3 链栈示意图

链栈的储存结构表示：
typedef struct StackNode{  
	int data;          //当前数据
	StackNode *next;  //指向下一个结点的指针
}StackNode,*StackList;

4.2 算法设计

（1）创建图

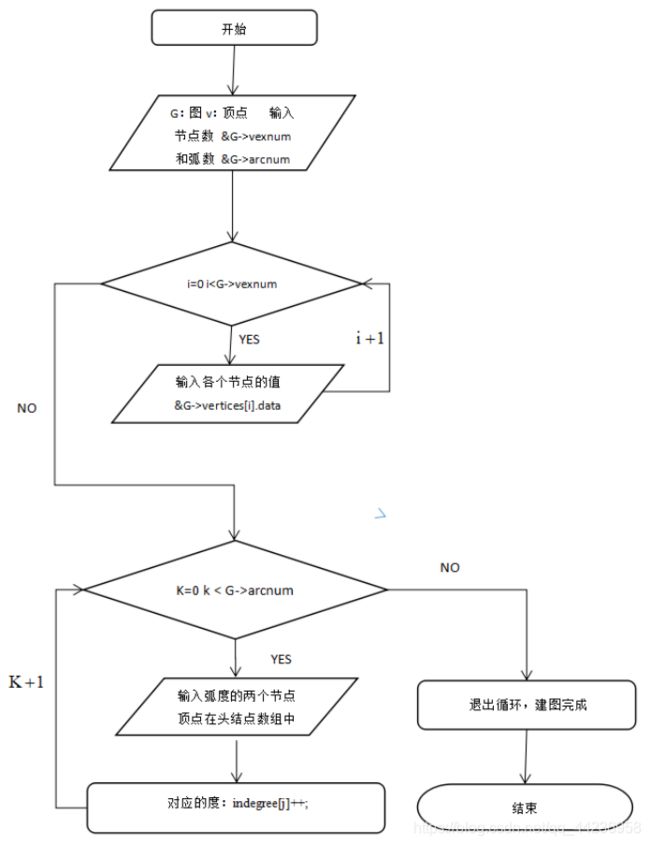
建立有向图：顶点在头结点数组中的定位，G带操作的图；v要在图中定位的顶；顶点存在则返回在头结点数组中的下标；否则返回图的定点数，邻接表初始化，输入有向图的边，对应顶点入度计数加1，如图4.4所示：

图 4.4 创建有向图的流程图

（2）栈的入栈出栈

入栈：入栈申请一个节点p.这个节点是用来存放入栈，将要放入的数e表示p->data，新节点后继为原栈顶节点，将新的结点p赋值给栈顶指针。流程图如图4.5所示：

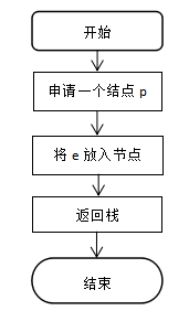
图 4.5 入栈的流程
出栈：实现入一个数据，立刻出去一个数据，因先判断栈是否为空，如果不为空，将栈的元素赋值给指针e，将旧栈顶指向新栈顶，即新的栈为空。流程图如图4.6所示：

图 4.6 出栈的流程

4.3拓扑排序

先声明栈指针S，并让其指向NULL。检查所有节点中是否有入度为0的节点，如果有，则进栈。之后当栈不为空的时候，先出栈，取出栈顶元素，并将其记录在topo[]数组中；让指针p指向记录出栈节点的第一条边的节点，将这个节点出度指向的所有节点的记录入度的indegree[]减一，当某个indegree为0的时候，进栈。
当栈为空的时候让最后一个topo元素为-1，最后检测topo[]数组中元素是否已经达到节点数，如果是，返回OK，达不到则返回ERROR，表示无法完全遍历，流程图如图4.7所示：

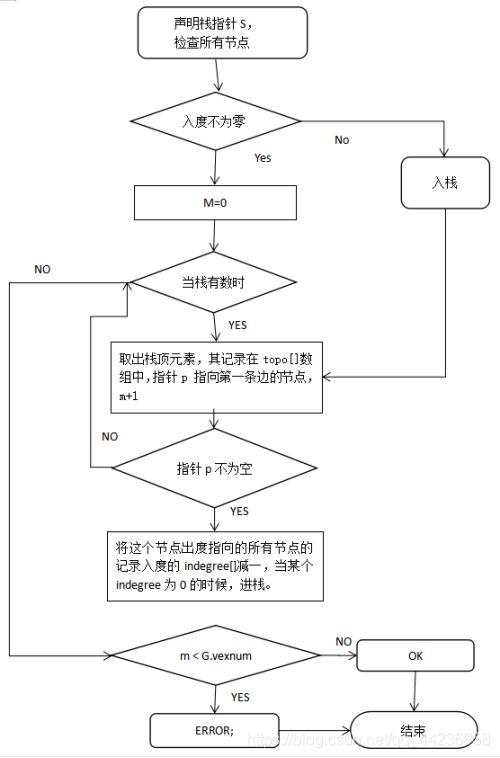
图 4.7 拓扑排序算法流程图

5程序编码(完整代码)

#include 
#include  
#define OK 1
#define ERROR 0
#define MVNum 100
typedef int Status;
typedef char VerTexType;
typedef char OtherInfo;
int indegree[MVNum] = {0};   
//创建栈 
typedef struct StackNode{  
	int data;
	StackNode *next;
}StackNode,*StackList;
//出栈函数 
StackList Pop(StackList S, int *e)
{
	StackList p;
	p = S;
	if (!p)
		return ERROR;
	*e = p->data;
	S = S->next;
	free(p);
	return S;
}
//入栈函数： 
StackList Push(StackList S,int e)
{
	StackList p;
	p = (StackNode *)malloc(sizeof(StackNode));
	p->data = e;
	p->next = S;
	S = p;
	return S;
}
//邻接表创建有向图的实现
//边结点 
typedef struct ArcNode{    //链表结点
	int adjvex;           //邻接表创建无向网的实现
	ArcNode *nextarc;    //指向下一条边的指针
	OtherInfo info;       //和边相关的信息
}ArcNode;
 
//顶点信息 
typedef struct VNode{   //头结点
	VerTexType data;   //顶点信息
	ArcNode *firstarc;//指向第一条依附该顶点的边的指针
}VNode,AdjList[MVNum];//AdjList 表示邻接表类型
 
typedef struct{
	AdjList vertices;     //邻接表头结点数组
	int vexnum, arcnum;   //图的顶点数和弧数
}ALGraph;
//创建有向图：
 
int LocateVex(ALGraph *G, VerTexType v)  //G带操作的图；v要在图中定位的顶点
{
	int i;
	for (i = 0; i < (G->vexnum); i++)
	{
		if (v == G->vertices[i].data)
			return i;               //顶点存在则返回在头结点数组中的下标；否则返回
	}
}
 
void CreateUDG(ALGraph *G)       
{
	int i, j, k;
	VerTexType v1, v2;
	ArcNode *p1;
	printf("输入总节点数和弧数："); //G带操作的图；v要在图中定位的顶点
	scanf("%d %d", &G->vexnum, &G->arcnum);
	fflush(stdin);    //是清空输入缓冲区的
	printf("输入各个节点的值：");  
	  for(i=0; i<G->vexnum;i++)   //邻接表初始化

{
  		scanf("%c", &G->vertices[i].data);
		G->vertices[i].firstarc = NULL;
		  }
for (k = 0; k < G->arcnum; k++)
	{
		fflush(stdin);   //是清空输入缓冲区的
		printf("弧度的两个点两个节点：");
		scanf("%c %c", &v1, &v2);
		i = LocateVex(G, v1);   //返回这两个顶点在顶点数组中的位置
		j = LocateVex(G, v2);
		p1 = (ArcNode *)malloc(sizeof(ArcNode));   //给邻接表指针分配空间
		p1->adjvex = j;                          //赋值给p->adjvex指向的顶点域
		p1->nextarc = G->vertices[i].firstarc; //nextarc指针域指向i结点的firstarc指针域  
		G->vertices[i].firstarc = p1;    //将点i的第一条指针指向
		indegree[j]++;       //vi->vj, vj入度加1
    }
}
//拓扑排序算法
Status TopologicalSort(ALGraph G, int *topo)
{ //先声明栈指针S，并让其指向NULL。检查所有节点中是否有入度为0的节点，如果有，则进栈。
	int i, m, k;
	StackList S;  //先声明栈指针S，并让其指向NULL。
	ArcNode *p;
	S = NULL;
	for (i = 0; i < G.vexnum; i++) //检查所有节点中是否有入度为0的节点，如果有则进栈。
	{
		if (!indegree[i])  //当数组不为零时  
			S=Push(S, i);
	}    //入度为零去完后 
	m = 0; //记录topu数组的数
	while (S)//栈不为空的时候，先出栈，取出栈顶元素，并将其记录在topo[]数组中
	{
		S=Pop(S, &i);
		topo[m] = i;
		++m;
		p = G.vertices[i].firstarc;   //指针p 指向第一条边的节点
		while (p != NULL)
		{
			k = p->adjvex; 
			--indegree[k];
			if (indegree[k] == 0)
				S=Push(S, k);
			p = p->nextarc;
		}
	}
	topo[m] = -1;  // 为-1时结束 
	if (m < G.vexnum)  // topo[]数组中元素是否已经达到节点数，
		return ERROR;     
	else
		return OK; 
}

int main(void)
{
	ALGraph G;
	int i;
	int topo[99] = {0};
	CreateUDG(&G);
	if (TopologicalSort(G, topo))
	{  printf("有向图，无环\n    拓扑排序序列为：");
		for (i = 0; topo[i] != -1; i++)
		{   
			printf("%c ", G.vertices[topo[i]].data);
		}
	}
	else
		printf("有环，请重新输入");
	printf("\n");
	return 0;
}

6程序调试与测试

（1）无环图的输入输出结果

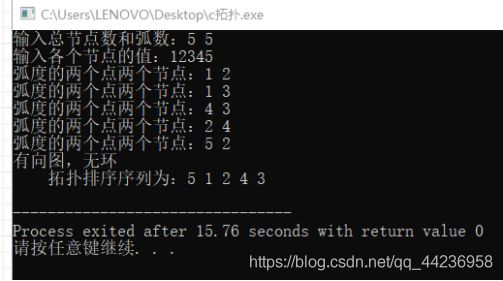
输入总节点数和弧数: 55
输入各个节点的值: 12345
弧度的两个点两个节点: 1 2
弧度的两个点两个节点:1 3
弧度的两个点两个节点: 4 3
弧度的两个点两个节点: 24
弧度的两个点两个节点: 5 2
有向图，无环
拓扑排序序列为:51243

无环结构图如图6.1 所示：

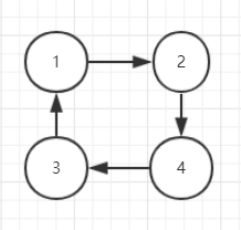
图6.1 有向有环图
输出如图6.2 所示：

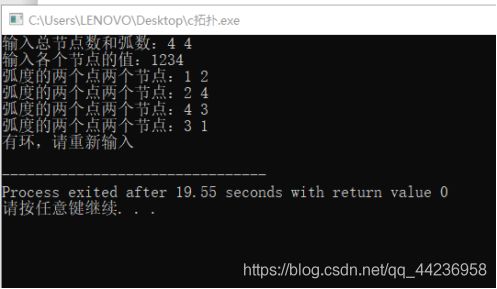
图6.2 有向有环图输出结果

（2）有环图的输入输出结果

输入总节点数和弧数: 44
输入各个节点的值: 1234
弧度的两个点两个节点: 1 2
弧度的两个点两个节点: 2 4
弧度的两个点两个节点: 4 3
弧度的两个点两个节点: 3 1
有环，请重新输入

有环结构图如图6.3 所示：

图6.3 有向无环图

输出结果如图6.4 所示：

图6.4 有向无环图输出结果

所得结果与预计结果一致

7结果分析

对于算法的时间复杂度和空间复杂度，拓扑排序实际是对有n个顶点和e条弧的有向图而言，建立求各顶点的入度的时间复杂度为O(e),空间复杂度O(e)；建零入度顶点栈的时间复杂度为O(n)；在拓扑排序过程中，若有向图无环，则每个顶点进一次栈、出一次栈，入度减1的操作在while语句中总共执行e次，所以空间复杂度s(n)=O(n+1)，总的时间复杂度为T(n)=O(n+e)。

8总结

本次课程设计，已经完成，判断有向图中是否存在回路，对于一个有向图，由键盘输入其顶点和弧的信息，采用邻接表将其保存图中。通过邻接表，建立有向图。通过栈进行弹出数据到数组，进行输出。
本次课程设计，我对拓扑排序和关键路径都有了更深的了解,和更加熟练的应用。以前根本就不了解拓扑排序是什么,现在知道拓扑排序是建立在有向无环图的基础上，而关键路径是建立在拓扑排序。
在上机实践中,我发现了自己的基础还不是很扎实。有些算法自己还是不能准确地写出来,有的时候还会因为空间分配等问题造成程序错误,遇到- -些较难的问题时,我还是要查看教材和其他的资料来帮助自己解决问题。这种习惯极好地补充了我在程序设计中不足的知识。这使我更深刻地体会到,学各种编译语言,不仅要动脑，更要动手去做。在以后的学习中,我会更加注重实践操作能力的培养，让自己的各方面能力都有所提高。

参考文献

[1] 严蔚敏.吴伟民.数据结构(C语言版)[M].北京：清华大学出版社,2017
[2] 李春葆.数据结构(C语言版)习题与解析[M].北京：清华大学出版社,2018
[2] 李军.程序设计基础(C语言版)[M].西安：西安电子科技大学出版社,2014