【金融数据分析】基于python实现的配对交易模型
配对交易——基于python实现
1.导入第三方库
import pandas as pd
import pandas_datareader.data as web
import datetime as dt
import statsmodels.formula.api as smf
from statsmodels.graphics.tsaplots import *
from statsmodels.tsa import stattools
from statsmodels.tsa.stattools import adfuller as ADF #导入ADF函数
from statsmodels.tsa.arima_model import ARIMA
import statsmodels.api as sm
import matplotlib.pyplot as plt
import numpy as np
import warnings
warnings.filterwarnings("ignore")#忽略警告
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号重点解释:pip导入pandas_datareader.data包用来获取两只或多只股票数据,最好是同一行业的两只股票
2.获取中国银行&中信银行股票数据
ChinaBank = web.DataReader('601988.SS', 'yahoo', dt.datetime(2009, 1, 2),
dt.datetime(2012, 12, 31))
ZXBank = web.DataReader('601998.SS', 'yahoo', dt.datetime(2009, 1, 2),
dt.datetime(2012, 12, 31))3.对比数据长度以及列名的重命名
m=pd.concat([ChinaBank['Close'],ZXBank['Close']],axis=1,join='inner')#数据长度不一致,合并数据
new_col = ['China', 'ZX']#列名重命名
m.columns = new_col
#获取收盘价
China_close = m['China']
ZX_close = m['ZX']4.对股票对数价格序列进行ADF相关性检验(配对交易一般使用对数价格)
# 中国银行股价数据
C_log = np.log(China_close)
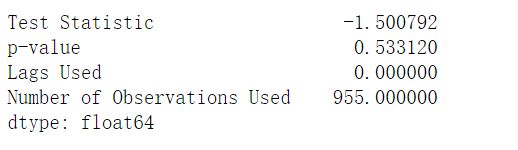
adf_C = ADF(C_log)
#将adf_C的信息转化为Series
result_C = pd.Series(adf_C[0:4],
index=[
'Test Statistic', 'p-value', 'Lags Used',
'Number of Observations Used'
])
print(result_C)ADF检验的P值一般小于0.05时,拒绝原假设。实际的p-value大于0.05,无法拒绝原假设,所以应该认为对数价格为非平稳序列。
对数价格不平稳,进行一阶差分(一般都会转为平稳价格序列)。
#一阶差分之后序列为平稳序列
ret_C=C_log.diff()[1:]
adf_ret_C=ADF(ret_C)#对一阶差分之后的数据作ADF检验
result_ret_C = pd.Series(adf_ret_C[0:4],
index=[
'Test Statistic', 'p-value', 'Lags Used',
'Number of Observations Used'
])
print(result_ret_C)p-vlaue<0.05,一阶差分ret_C为平稳序列,中国银行对数价格再作一阶差分之后的序列数据为一阶单整序列。
中信银行数据处理方式同,就不赘述了,直接上代码。
# 中信银行股价数据
ZX_log=np.log(ZX_close)
adf_ZX = ADF(ZX_log)
#将adf_C的信息转化为Series
result_ZX = pd.Series(adf_ZX[0:4],
index=[
'Test Statistic', 'p-value', 'Lags Used',
'Number of Observations Used'
])
print(result_ZX)
#一阶差分之后序列为平稳序列。
ret_ZX=ZX_log.diff()[1:]
adf_ret_ZX=ADF(ret_ZX)#对一阶差分之后的数据作ADF检验
result_ret_ZX = pd.Series(adf_ret_ZX[0:4],
index=[
'Test Statistic', 'p-value', 'Lags Used',
'Number of Observations Used'
])
print(result_ret_ZX)
5.若两只股票价格序列相关性较大,则可以对两只股票进行配对,同时需要价差进行平稳性检验。
#中国银行与浦发银行对数价格(收益率)时序图
plt.figure(figsize =(15,10))
C_log.plot(label='601988',style='--')
ZX_log.plot(label='601998',style='-')
plt.legend(loc ='upper left')
plt.title('中国银行------中信银行的对数价格时序图')图像说明对数价格有稳定性。但整个序列是不稳定的,采用一阶差分数据。
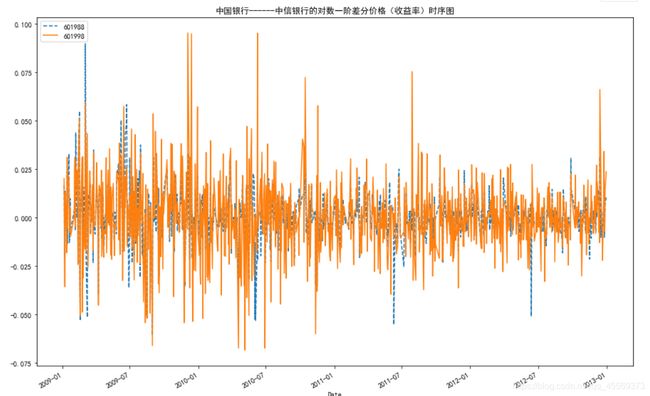
#中国银行与浦发银行对数价格(收益率)时序图
plt.figure(figsize =(15,10))
ret_C.plot(label='601988',style='--')
ret_ZX.plot(label='601998',style='-')
plt.legend(loc ='upper left')
plt.title('中国银行------中信银行的对数一阶差分价格(收益率)时序图')对数价格一阶差分数据是平稳序列,可以对两只银行股票的协整关系检验(回归分析)。只有当残差平稳时,两只股票具有具有协整关系。
model = sm.OLS(ZX_log,sm.add_constant(C_log))
results = model.fit()
print(results.summary())求回归直线的残差
#对回归残差进行平稳性检验
alpha=results.params[0] #提取回归截距
beta=results.params[1] # 提取回归系数
spread=ZX_log-beta*C_log-alpha #求残差序列
spread.head()
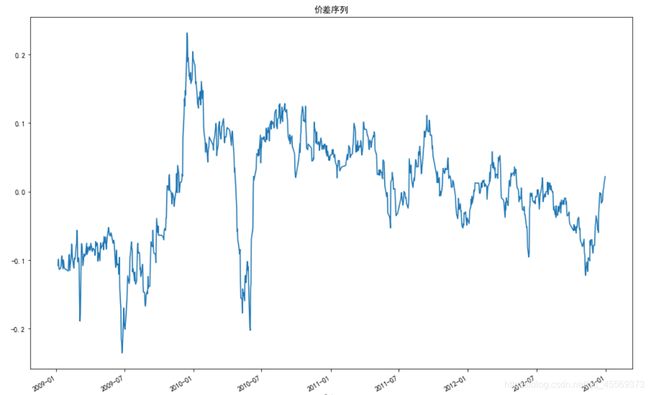
#残差序列图
plt.figure(figsize=(15,10))
spread.plot()
plt.title('价差序列')图像貌似是说残差不是稳定时间序列,不过还是要经过ADF检验的p-value值说明问题。(一般是平稳的,只是图像看起来不平稳)
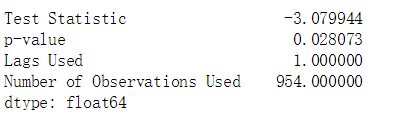
result_sp = pd.Series(adf_Spread[0:4],
index=[
'Test Statistic', 'p-value', 'Lags Used',
'Number of Observations Used'
])
print(result_sp)p-value值为:0.028<0.05,接受原假设。所以残差序列平稳,这两只股票可以配对交易。
下次再更...