GMM模型和EM算法

GMM模型和EM算法

高斯混合模型GMM

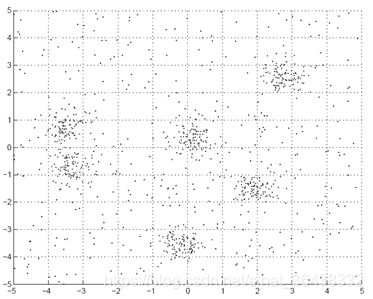
上图的分布很难用一个高斯分布进行模拟。观察上图，大致可以看见6个分布。将6个高斯分布线性加到一起就组成了能描述上图的高斯混合分布。

混高斯合分布的概率密度函数如下：
$$\begin{array}{l}p(x|\theta )=\sum _{j=1}^{K}p(x,z=j|\theta )=p(z=j|\theta )p(x|z=j,\theta )=\sum _{j=1}^K{\pi }_{j}N\left(x;{\mu }_j,{\Sigma }_j\right)\\ \\ \\ 其中:p(z=j|\theta )={\pi }_j;p(x|z=j,\theta )=N\left(x;{\mu }_j,{\Sigma }_j\right)\\ \theta \equiv \left\{{\pi }_j,{\mu }_j,{\Sigma }_j;j=1,2,\dots ,K\right\};j=1,2,\dots ,K\end{array}$$
对于高斯混合模型的参数估计，如果利用最大似然估计，即：
$${\theta }^{\ast }={\mathrm{argmax}}_{\theta }\prod _{i=1}^{N}p\left(x_i|\theta \right)$$
对似然函数取对数，求解最优化问题(求导数为0)：
$$\begin{array}{rl}l(\theta ;x)=\log p(x|\theta )& =\log \prod _{i}p\left(x_i|\theta \right)\\ & =\sum _i\log p\left(x_i|\theta \right)\\ & =\sum _i\log \sum _{z}p\left(x_i,z|\theta \right)=0\end{array}$$
log函数里面有个求和符号，很难求导来求最优值。因此最大似然估计难以进行GMM的参数估计。

EM算法(Expectation-Maximization Algorithm)

观察上面那副图我们可以大致地看出有6个高斯分布。如果对于上图地每一个点，能够大致的地判断它属于这六个高斯分布中的哪一个，即为这些点贴上“标签”z，然后对于每个高斯分布，利用我们认为属于该分布的点估计参数，这样就能够得出这个高斯混合分布的参数了。这就是EM算法的直观理解。而这些“标签”z可以认为是分布的隐含变量(当然，这些标签可以是“软划分”，即属于某个高斯分布的概率)。

回到上文的对数似然函数：
$$\begin{array}{r}l(\theta ;x)=\sum _i\log \sum _{z}p\left(x_i,z|\theta \right)\end{array}$$
其中：
$$\log \sum _{z}p(x,z|\theta )=\log \sum _{z}q(z)\frac{p(x,z|\theta )}{q(z)}\ge \sum _{z}q(z)\log \frac{p(x,z|\theta )}{q(z)}（根据Jensen不等式）$$
为了下面表示方便，令：
$$\begin{gathered} L(\theta ;x)=\sum _i\sum _{z}q(z)\log \frac{p(x,z|\theta )}{q(z)} \\ l(\theta ;x)\ge L(\theta ;x) \end{gathered}$$

如果我们能根据Jensen不等式放缩这个似然函数，求和符号就挪到了log函数外面，这样就能更好求导来求解最优值。Jensen不等式：
$$\text{ Jensen’s inequality: }f\left(\sum _j{\lambda }_j{x}_j\right)\ge \sum _j{\lambda }_{j}f\left(x_j\right)$$
但是，这个q(z)该是多少呢？结果证明，q(z)=p(z|x,θ)时最好，因为此时式子的等号成立：
$$\begin{array}{l}\sum _{z}p\left(z|x,\theta \right)\log \frac{p\left(x,z|\theta \right)}{p\left(z|x,\theta \right)}\\ =\sum _{z}p\left(z|x,\theta \right)\log p\left(x|\theta \right)\\ =\log p\left(x|\theta \right)\\ =\sum _{z}p\left(x_i,z|\theta \right)\end{array}$$

所以，E步就是利用目前的参数θ来，根据q(z)=p(z|x,θ)来计算q(z)，使得(也就是说，当q(z)=p(z|x,θ)时，下式取最优值):
$$q^{(t+1)}=\arg \underset{q}{\max }L\left(q,{\theta }^{(t)}\right)$$
M步就是利用L(θ|x)来近似l(θ|x)，求解最优化问题计算θ：
$${\theta }^{(t+1)}=\arg \underset{q}{\max }L\left(q^{(t)},\theta \right)$$

$$\begin{array}{rl}L(q,\theta )& =\sum _{i=1}^N\sum _{z_i}q\left(z_i\right)\log \frac{p\left(x_i,z_i|\theta \right)}{q\left(z_i\right)}\\ & =\sum _{i=1}^N\sum _{z_i}q\left(z_i\right)\log p\left(x_i{z}_i|\theta \right)-q\left(z_i\right)\log q\left(z_i\right)\\ & =\sum _{i=1}^N\sum _{j=1}^K{q}_{ij}\log \left[{\pi }_j\ast p\left(x_i|{\phi }_j\right)\right]+C(-qlogq可以看作是常数)\end{array}$$

其中，φj表示混合分布中，第j个高斯分布的参数(μ,Σ)，这里为了简便而统一表示。πj即高斯混合分布公式中每个高斯分布的权重，即：
$$\begin{array}{rl}& p(z=j|\theta )={\pi }_j;\\ & p(x|z=j,\theta )=p\left(x|{\phi }_j\right)\end{array}$$
对于φj，将L求导等于零即可求得：
$$\frac{\partial L(q,\theta )}{\partial {\phi }_j}=\frac{\partial \left\{\sum _{i=1}^N{q}_{ij}\log p\left(x_i|{\phi }_j\right)\right\}}{\partial {\phi }_j}=0\Rightarrow {\phi }_j$$
而对于πj，还满足于一个约束条件：
$$\sum _{j=1}^K{\pi }_j=1$$
因此需要利用拉格朗日乘子求解。

在回到E步，之前说我们用z表示"标签"，对于某一个高斯分布，q(z)=p(z|x,θ)具体公式如下：
$$q\left(z_i=c\right)=p\left(z_i=c|x_i,{\theta }^t\right)=\frac{p\left(x_i,z_i=c|{\theta }^t\right)}{{\sum }_{d}p\left(x_i,z_i=d|{\theta }^t\right)}$$
对于GMM模型来说：
$$q\left(z_i=c\right)=\frac{\pi \left(z_i=c\right)N\left(x_i|{\mu }_{c,{\sigma }_c}\right)}{{\sum }_d\pi \left(z_i=d\right)N\left(x_i|{\mu }_d,{\sigma }_d\right)}$$