编辑距离的计算和过程打印

      转载请注明出处，http://www.cnblogs.com/fangpei/p/3570512.html 。

      上学期选了王老师的《现代信息检索》的课程，在“词典及容错式检索”中说到了编辑距离，计算编辑距离使用了动态规划的方法，感觉很有意思，于是实现了一下。

      编辑距离的定义：

      是指两个字串之间，由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。

      例如将akitten转成sitting：

            kitten （a→ ）

            sitten （k→s）

            sittin （e→i ）

            sitting （→g）

       则编辑距离为4。

       下面写出代码：

 1 //Written by fangpei
 2 //Find the editdistance between two strings, and print the steps of change 
 3 #include
 4 #include<string>
 5 using namespace std;
 6 
 7 int Min_m(int m0, int m1, int m2);
 8 void Print_step(int m[][40][4], string s1, string s2, int len1, int len2);
 9 
10 int main()
11 {
12     string s1, s2;
13     cin >> s1 >> s2;
14     int i, j;
15     int len1 = s1.length();
16     int len2 = s2.length();
17     int m[40][40][4] = {0};
18     for (i = 1; i <= len1; ++i) {
19         m[i][0][1] = i;
20         m[i][0][3] = i;
21     }
22     for (j = 1; j <= len2; ++j) {
23         m[0][j][2] = j;
24         m[0][j][3] = j;
25     }
26     for (i = 1; i <= len1; ++i) {
27         for (j = 1; j <= len2; ++j) {
28             if (s1[i-1] == s2[j-1])
29                 m[i][j][0] = m[i-1][j-1][3]; //copy(cost 0)
30             else 
31                 m[i][j][0] = m[i-1][j-1][3] + 1; //replace(cost 1)
32             m[i][j][1] = m[i-1][j][3] + 1;  //delete(cost 1)
33             m[i][j][2] = m[i][j-1][3] + 1;  //insert(cost 1)
34             // the least cost until this step
35             m[i][j][3] = Min_m(m[i][j][0], m[i][j][1], m[i][j][2]);  
36         }
37     }
38     cout << m[len1][len2][3] << endl;
39     Print_step(m, s1, s2, len1, len2);
40     return 0;
41 }
42 
43 int Min_m(int m0, int m1, int m2) //find the min of m[i][j][*]
44 {
45     if (m0 > m1)
46         m0 = m1;
47     if (m0 > m2)
48         return m2;
49     return m0;
50 }
51 
52 //print the change step in detail
53 void Print_step(int m[][40][4], string s1, string s2, int len1, int len2) 
54 {
55     while (len1 !=0 || len2 != 0) {  
56         //copy(cost 0)
57         if (m[len1][len2][3] == m[len1][len2][0] && 
58             m[len1][len2][0] == m[len1-1][len2-1][3]) {
59             cout << "copy    '" << s1[len1-1] << "' to '" << 
60                  s2[len2-1] << "', cost 0" << endl;
61             --len1;
62             --len2;
63         }
64         //replace(cost 1)
65         else if (m[len1][len2][3] == m[len1][len2][0] && 
66                  m[len1][len2][0] == m[len1-1][len2-1][3] + 1) {
67             cout << "replace '" << s1[len1-1] << "' to '" << 
68                  s2[len2-1] << "', cost 1" << endl;
69             --len1;
70             --len2;
71         }
72         //delete(cost 1)
73         else if (m[len1][len2][3] == m[len1][len2][1] && m[len1][len2][1] != 0) {
74             cout << "delete  '" << s1[len1-1] << "' to " << " * , cost 1" << endl;
75             --len1;
76         }
77         //insert(cost 1)
78         else if (m[len1][len2][3] == m[len1][len2][2] && m[len1][len2][2] != 0) {
79             cout << "insert   *  to '" << s2[len2-1] << "', cost 1" << endl;
80             --len2;
81         }
82     }
83 }

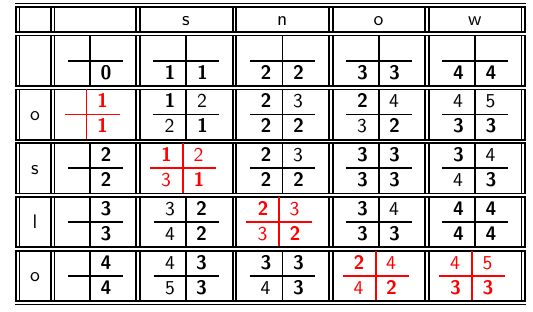
      上面动态规划算法的步骤过程用矩阵来表达，比较对应的字符。

      第一行和第一列：

            都按照等差数列递增；（见下面的例子）

      其余元素：

            内部左上角数字：

                  如果行列对应的两个字符相等，则赋值为左上角元素的内部右下角数字的值； 

                  如果行列对应的两个字符不相等，则赋值为左上角元素的内部右下角数字的值加1； 

            内部右上角数字：

                  赋值为上方元素的内部右下角数字加1；

            内部左下角数字：

                  赋值为左方元素的内部右下角数字加1；

            内部右下角数字：

                  赋值为内部另外三个数字的最小值。

      最后求得的矩阵最右下角的数字为两个字符串的编辑距离。

 

      详细的讲解参考《信息检索导论》（第5次印刷）第40页。

      王老师讲的一个例子：

                           

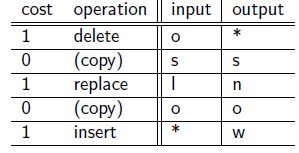
      编辑距离变换步骤如下：

                           

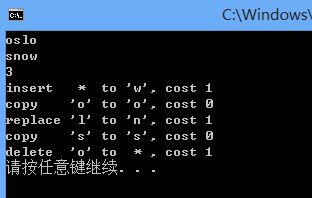
      我的程序运行的结果（是上面变换步骤的倒序）：

                            

 

转载于:https://www.cnblogs.com/fangpei/p/3570512.html