数据结构&算法-----（1）常用数据结构

“数据结构是算法的基石”

数组（Array ）

数组的优点：

• 构建非常简单
• 能在 O(1) 的时间里根据数组的下标（index）查询某个元素

数组的缺点：

• 构建时必须分配一段连续的空间
• 查询某个元素是否存在时需要遍历整个数组，耗费 O(n) 的时间（其中，n 是元素的个数）
• 删除和添加某个元素时，同样需要耗费 O(n) 的时间

常用解题方法：
设置两个指针，分别指向不同的位置，不断调整指针指向来实现O（N）时间复杂度内实现算法。

常见的面试题目：

• 调整数组顺序使奇数位于偶数前面
• 拼接一个最大/小的数字
• 合并两个有序数组
• 查找多数元素
• 数组中的重复元素

调整数组顺序使奇数位于偶数前面

题目描述：
调整数组顺序使奇数位于偶数前面。输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有奇数位于数组的前半部分，所有偶数位于数组的后半部分。

思路：
关于数组的操作，我们首先考虑使用双指针。使用left和right指针，left指针从前往后移动，直到遇到偶数。right指针向前移动，直到遇到一个奇数。交换两个指针所指向的元素。通过多次交换来实现顺序的调整。

算法实现：

	/**
     * 可以满足奇数位于偶数前面的算法，但是奇数和奇数、偶数和偶数的相对位置不能保证。
     * 时间复杂度O(N)，空间O(1)
     * @param arr
     */
    private static void reOrderArray(int[] arr){
        if(arr==null||arr.length<2)
            return ;
            
        int left = 0;
        int right = arr.length-1;
        
        while(left<right){
        
        	//奇数&1 == 1
            while( (arr[left]&1) ==1){
                left++;
            } 
            
            //偶数&1 == 0
            while( (arr[right]&1) ==0){
                right--;
            }
            
            // 如果不加此处的if判断语句，会导致right已经在left前面了，但是依然进行了交换。
            // 即将已经在前面的奇数和后面的偶数进行了置换！！！
            if(left<right){
                int temp = arr[left];
                arr[left] = arr[right];
                arr[right] = temp;
            }
        }
    }

字符串（String）

字符串相关高频的算法题目包括：

• 最长不含重复元素的子串
• 最长公共子序列（参见下面例题）
• 最长公共子串 （动态规划，参见第六节举例 ：最长公共子串）
• 最长递增子序列 （动态规划， 例题分析 LeetCode300）
• 最长公共前缀
• 自定义函数实现字符串转整数的功能

子串和子序列的区别：
子串：字符串中任意个连续的字符组成的子序列。
子序列：字符串中按照前后顺序取出的任意个字符组成，不要求连续。

LeetCode3. 无重复字符的最长子串。最长不重复子串（ByteDance二面）

算法题目：
请从字符串中找出一个最长的不包含重复字符的子字符串，计算该最长子字符串的长度。假设该字符串中只包含‘a’-'z’的字符。
例如，给出字符串abcabcbb，那么符合要求的字串为abc，其长度为3。

给定一个字符串，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:
输入: "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:
输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:
输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

算法思路：
可以使用HashMap和双指针来实现该算法。HashMap中不断更新维护每个字符出现的位置。使用count变量进行计数，当统计的最长子字符串被重复字符破坏时，比较count和max的大小，判断是否需要更新max变量。不管是哪种情况，每次都需要更新map中的信息，并且需要更新count变量。

算法实现：

import java.util.HashMap;
import java.util.Map;

/**
 *  求最长不含重复字符的子字符串
 */
public class Main {
    public static void main(String[] args) {
        System.out.println(lengthOfLongestSubstring("arbacacfr"));
        System.out.println(lengthOfLongestSubstring("hkcpmprxxxqw"));
        System.out.println(lengthOfLongestSubstring("dvdf"));
        System.out.println(lengthOfLongestSubstring("tmmzuxt"));
        System.out.println(lengthOfLongestSubstring("jbpnbwwd"));

    }

    public static int lengthOfLongestSubstring(String s) {
        if(s==null||s.length()==0)
            return 0;
        // 建立一个HashMap用来存放字符和位置信息
        Map<Character,Integer> map = new HashMap<Character, Integer>();
        int max = 0; // 用来记录最大值
        int count = 0; // 用来统计长度
        char[] c = s.toCharArray();
        for(int i=0; i<c.length; i++){
            if(!map.containsKey(c[i])){
                map.put(c[i], i);
                count++;
            }else {
                // 若map中已经包含该字符，分为两种情况讨论
                Integer index = map.get(c[i]);
                // 情况1：上次出现的该字符并不在当前所统计的最长字符串中，只需要更新位置信息。并且统计count++
                if(i-index>count){
                    count++;
                    map.put(c[i], i);
                    continue;
                }
                // 情况2：上次出现的该字符影响了当前最长不重复的子字符串
                // 则更新位置信息、max变量和count计数
                map.put(c[i], i);
                if(count>max){
                    max = count;
                }
                count = i - index;
            }
        }
        // 防止出现没有重复字符的情况，此时max = 0
        return max>count?max:count;
    }
}

if(i-index>count)
和
count = i - index;
容易出错， 小心

滑动窗口解法：

什么是滑动窗口？
其实就是一个队列，比如例题中的 abcabcbb，进入这个队列（窗口）为 abc 满足题目要求，当再进入 a，队列变成了 abca，这时候不满足要求。所以，我们要移动这个队列！
如何移动？
我们只要把队列的左边的元素移出就行了，直到满足题目要求！
一直维持这样的队列，找出队列出现最长的长度时候，求出解！

    private static int lengthOfLongestSubstring(String s) {
        if(s==null||s.length()==0)
            return 0;
        HashMap<Character, Integer> map = new HashMap<Character, Integer>();
        int max = 0;
        int left = 0;
        for (int i=0; i<s.length(); i++) {
            if(map.containsKey(s.charAt(i))){
            	//遇到重复的字符时，找出窗口最左端的元素位置 left = map.get(s.charAt(i)) + 1
                left = Math.max(left, map.get(s.charAt(i)) + 1);
            }
            map.put(s.charAt(i), i);
            max = Math.max(max, i-left+1);
        }
        return max;
    }

最长公共子序列

题目描述：
给定两个不字符串，求出最长公共子序列。

思路：
可以使用递归的方式来实现该算法。我们先比较字符下标为0的位置是否相等，根据两种情况分别进行后续的递归。画图分析如下：

情况一：

情况二：

算法实现：

	/**
     * 最长公共子序列，返回值为长度
     * @param x
     * @param y
     * @return
     */
    int longestPublicSubSequence(String x, String y){
    	//递归，首先需要确定递归结束的条件
        if(x.length() == 0 || y.length() == 0){
            return 0;
        }
        
        if(x.charAt(0) == y.charAt(0)){
            return 1 + longestPublicSubSequence(x.substring(1), y.substring(1));
        }else{
            return Math.max(longestPublicSubSequence(x.substring(1), y.substring(0)), 
                    longestPublicSubSequence(x.substring(0), y.substring(1)));
        }
	}
	
	// 返回从beginIndex开始，到字符串结尾的字符串。
	public String substring(int beginIndex)

LeetCode 第 242 题：给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词

示例 1:
输入: s = "anagram", t = "nagaram"
输出: true

示例 2:
输入: s = "rat", t = "car"
输出: false

你可以假设字符串只包含小写字母。

    public boolean isAnagram(String s, String t) {

        //如果 s 和 t 的长度不同，t 不能是 s 的变位词，可以提前返回。
        if (s.length() != t.length()) {
            return false;
        }

		有点桶排序的意思
        int[] counter = new int[26];

        for (int i = 0; i < s.length(); i++) {
            counter[s.charAt(i) - 'a']++;
            counter[t.charAt(i) - 'a']--;
        }

        for (int count : counter) {
            if (count != 0) {
                return false;
            }
        }

        return true;
    }

大数求和

如果给出两个很大很大的整数，这两个数大到long类型也装不下，比如100位整数，如何求它们的和呢？
参考文章：
怎样实现大整数相加？
大数求和（string）

    private static String bigNumberSum(String s1, String s2) {
        String ans;

        char[] max=s1.toCharArray(), min=s2.toCharArray();
        if (s1.length()<s2.length()) {
            max=s2.toCharArray();
            min=s1.toCharArray();
        }

        for (int i=min.length-1, j=max.length-1; i>=0; i--, j--) {
            //将min的所有位加到max的对应位上
            max[j]+=min[i]-'0';
        }

        for (int i=max.length-1; i>0; i--) {
            if (max[i]>'9') {
                max[i]-=10;
                max[i-1]++;
            }
        }

        if (max[0]>'9') {
            max[0]-=10;
            ans='1'+String.valueOf(max);
        } else {
            ans = String.valueOf(max);
        }

        return ans;
    }

    public static String bigNumberSum2(String s1, String s2) {

        //1.把两个大整数用数组【逆序存储】，数组长度等于较大整数位数+1
        int maxLength = s1.length() > s2.length() ? s1.length() : s2.length();

        int[] arrayA = new int[maxLength+1];
        for(int i=0; i<s1.length(); i++){
            arrayA[i] = s1.charAt(s1.length()-1-i) - '0';
        }

        int[] arrayB = new int[maxLength+1];
        for(int i=0; i<s2.length(); i++){
            arrayB[i] = s2.charAt(s2.length()-1-i) - '0';
        }

        //2.构建result数组，数组长度等于较大整数位数+1
        int[] result = new int[maxLength+1];

        //3.遍历数组，按位相加
        for(int i=0; i<result.length; i++) {
            //加上前一位的进位
            int temp = result[i];
            temp += arrayA[i];
            temp += arrayB[i];

            //如果有进位
            if(temp >= 10){
                temp = temp-10;
                result[i+1] = 1;
            }

            result[i] = temp;
        }

        //4.把result数组再次逆序并转成String
        StringBuilder sb = new StringBuilder();

        //用于标记是否找到大整数的最高有效位
        boolean findFirst = false;

        //从后往前
        for (int i=result.length-1; i>=0; i--) {
            if(!findFirst) {
                //用于跳过结果数组末尾的0
                if(result[i] == 0) {
                    continue;
                }
                findFirst = true;
            }
            sb.append(result[i]);
        }

        return sb.toString();
    }

链表（LinkedList）

链表结点定义：

class Node{  
    int val;  
    Node next;  
    public Node(int val){  
         this.val=val;  
    }
} 

链表的优点：

• 链表能灵活地分配内存空间；
• 能在 O(1) 时间内删除或者添加元素，前提：元素的前一个元素已知（在双链表中：元素的后一个元素已知）。

链表的缺点：

• 不像数组能通过下标迅速读取元素，每次都要从链表头开始一个一个读取；
• 查询第 k 个元素需要 O(k) 时间。

应用场景：
链表：数据元素个数不确定，需要经常进行数据的添加和删除
数组：数据元素个数确定，查询多，删除插入少

经典解法：

1. 利用快慢指针（有时候需要用到三个指针）
   典型题目例如：链表的翻转，寻找倒数第 k 个元素，寻找链表中间位置的元素，判断链表是否有环等等。
   常用prev，curr，next（为区别next.next可以使用lat，则lat.next）
2. 构建一个虚假的链表头
   常用于头节点需要改变的链表，用dummy，最后返回dummy.next

建议&注意：

• 在白板上画出节点之间的相互关系，然后画出修改的方法
• 结点连接时注意先后顺序
• 注意使用 ListNode dummy = new ListNode(-1); 返回dummy.next
• 注意循环指针指向和复位

链表常见算法题：

• 单链表反转
• 合并有序单链表
• 找出单链表的中间节点
• 判断单链表相交或者有环
• 找出进入环的第一个节点
• 求单链表相交的第一个节点

单链表反转

1→2→3→4→5，反转之后返回5→4→3→2→1

反转步骤：

• 从头到尾遍历原链表，每遍历一个结点
• 将其摘下放在新链表的最前端。
• 注意链表为空和只有一个结点的情况。

public static Node reverseNode(Node head){  
      // 如果链表为空或只有一个节点，无需反转，直接返回原链表表头  
      if(head == null || head.next == null)  
          return head;  
          
      Node reHead = null;  
      Node cur = head;  
      
      //保存当前结点
      while(cur!=null){  
          Node reCur = cur;      // 用reCur保存住对要处理节点的引用  
          cur = cur.next;        // cur更新到下一个节点  
          reCur.next = reHead;   // 更新要处理节点的next引用  
          reHead = reCur;        // reHead指向要处理节点的前一个节点  
      }  
      
      return reHead;  
 }
 
这种方法不好记, 参见LeetCode25题解法，如下：

    public ListNode reverseLinkedList(ListNode head) {

		// 如果链表为空或只有一个节点，无需反转，直接返回原链表表头  
		if(head == null || head.next == null)  
			return head;  

        ListNode pre = null;
        ListNode curr = head;
        
        //保存下一个结点
        while (curr != null) {
            ListNode next = curr.next;
            curr.next = pre;
            pre = curr;
            curr = next;
        }
        
        return pre;
    }

合并两个有序的单链表

给出两个分别有序的单链表，将其合并成一条新的有序单链表。
举例：1→3→5和2→4→6合并之后为1→2→3→4→5→6

步骤：

• 首先，我们通过比较确定新链表的头节点，然后移动链表1或者链表2的头指针。
• 然后通过递归来得到新的链表头结点的next

public static Node mergeList(Node list1 , Node list2){  
    if(list1==null)  
        return list2;  
    if(list2==null)  
        return list1;  
        
    Node resultNode;  
    
    if(list1.val<list2.val){ // 通过比较大小，得到新的节点 
        resultNode = list1;  
        list1 = list1.next;  
    } else {  
        resultNode = list2;  
        list2 = list2.next;  
    }  
    
    // 递归得到next
    resultNode.next = mergeList(list1, list2);  
    return resultNode;  
}

找出单链表的中间节点

public static void FindMid(ListNode head){
    ListNode fast = head;
    ListNode slow = head;
    while((fast != null)&&(fast.next != null)){
        fast = fast.next.next;
        slow = slow.next;
    }
    System.out.println(slow.data);
}

LeetCode 第 25 题：链表，每 k 个节点一组进行翻转

链表翻转算法：

    public ListNode reverseLinkedList(ListNode head) {

		// 如果链表为空或只有一个节点，无需反转，直接返回原链表表头  
		if(head == null || head.next == null)  
			return head;  

        ListNode pre = null;
        ListNode curr = head;
        
        while (curr != null) {
            ListNode next = curr.next;
            curr.next = pre;
            pre = curr;
            curr = next;
        }
        
        return pre;
    }

LeetCode25题解，同start和end指针指向每次要翻转的首尾节点：

    //当k=2时：
    //  pre       start     end      next
    // dummy   ->   1   ->   2   ->   3   ->   4   ->   5   ->   null
    public ListNode reverseKGroup(ListNode head, int k) {
        ListNode dummy = new ListNode(-1);
        dummy.next = head;
        ListNode pre = dummy;
        ListNode end = dummy;
        while (end.next != null) {
            for (int i = 0; i < k && end != null; i++) {
                end = end.next;
            }
            if (end == null)
                break;
            ListNode start = pre.next;
            ListNode next = end.next;
            //翻转前预处理
            end.next = null;
            //翻转，并重新链接链表
            pre.next = reverseLinkedList(start);
            start.next = next;
            //复位, 需要注意翻转后start在最后,赋值给pre
            pre = start;
            end = pre;
        }
        return dummy.next;
    }

LeetCode 第 24 题：两个一组翻转链表

（主要是在白板上找规律，也晒一下代码吧）
题目很经典，注意复位时prevNode和head的细节处理。

    public ListNode swapPairs(ListNode head) {

        ListNode dummy = new ListNode(-1);
        dummy.next = head;

        ListNode prevNode = dummy;

        while ((head != null) && (head.next != null)) {

            ListNode firstNode = head;
            ListNode secondNode = head.next;

            prevNode.next = secondNode;
            firstNode.next = secondNode.next;
            secondNode.next = firstNode;

            //复位
            prevNode = firstNode;
            head = firstNode.next;
        }

        return dummy.next;

    }

链表连接时先在白板上画出，找出先后顺序！！！

idea：
在链表的循环中，有时候不知道是判断curr！=null还是curr.next！=null还是都需要判断，这个得根据业务逻辑来推定，可以先尝试写一个（不要求一定对），后根据业务代码修改。

栈（Stack）

实现：
利用一个单链表可以实现栈的数据结构。
而且，只针对栈顶元素进行操作，所以借用单链表的头就能让所有栈的操作在 O(1) 的时间内完成。

包含min函数的栈

题目描述：
定义栈的数据结构，请在该类型中实现一个能够得到栈最小元素的min函数。在该栈中，调用min、push和pop方法，且各个函数的时间复杂度均为O(1)。

算法思路：
题目要求我们的各个方法均为O(1)复杂度，我们考虑增加辅助空间来实现，即增加一个专门用来存储min值的辅助栈。

实现步骤：

• 比如，data依次入栈：5, 4, 3, 8, 10, 11, 12, 1。则辅助栈依次入栈：5, 4, 3，no，no, no, no, 1。其中，no代表此次不入栈。也就是说每次入栈的时候，如果入栈的元素比min中的栈顶元素小或等于则入栈，否则不入栈。
• 当出栈的时候，我们比较辅助栈与当前出栈的值是否相等。如果相等，则辅助栈栈顶元素也需要出栈。
• 当需要获取栈中最小元素的时候，我们直接获取到辅助栈的栈顶元素即可。

算法实现：

import java.util.Stack;   
public class Main {  

    Stack<Integer> stack = new Stack<>();  
    Stack<Integer> minStack = new Stack<>();  

	/** 
	 * 首先需要对stack执行入栈操作, 
	 * 判断minStack中是否需要入栈操作 
	 */  
    public void push(int node) {  
        stack.push(node);  
        if(minStack.isEmpty()||minStack.peek()>=node)  
            minStack.push(node);  
    }  

	/** 
	 * 判断minStack中是否需要出栈操作 
	 */  
    public void pop() {   
        if(stack.peek()==minStack.peek()){  
            minStack.pop();  
        }  
        stack.pop();
    }  

    public int top() {  
        return stack.peek();  
    }  

	/** 
	 * 直接peek minStack 
	 * @return 
	 */  
    public int min() {  
        return minStack.peek();  
    }  
}

这里需要注意的是，在获取栈中的min值时，我们应该使用minStack.peek方法而不是minStack.pop方法。peek方法仅仅是获取数值，但是pop方法则会执行出栈操作。

LeetCode 第 739 题：气温列表

根据每日气温列表，请重新生成一个列表，对应位置的输入是你需要再等待多久温度才会升高超过该日的天数。如果之后都不会升高，请在该位置用 0 来代替。

更好理解的代码：

    public int[] dailyTemperatures(int[] T) {
        int length = T.length;
        int [] ans = new int[length];
        Stack<Integer> stack = new Stack<Integer>();
        /**
         * 73, 74, 75, 71, 69, 72, 76, 73
         */
         //用for(int i=length-1; i>=0; i--)感觉不太好理解，也可以做。
        for (int i=0; i<length; i++) {
            while (!stack.isEmpty() && T[i] > T[stack.peek()]) {
                int index = stack.pop();
                ans[index] = i-index;
            }
            stack.push(i);
        }
        return ans;
    }

利用堆栈，还可以解决如下常见问题：（记得刷！！！）
求解算术表达式的结果（LeetCode 224困难、227中等、772、770)
求解直方图里最大的矩形区域（LeetCode 84）

---

LeetCode 第 227 题：字符串表达式计算器

实现一个基本的计算器来计算一个简单的字符串表达式的值。
字符串表达式仅包含非负整数，+， -， *， / 四种运算符和空格 。 整数除法仅保留整数部分。
输入: " 3+5 / 2 "
输出: 5
这题好像是数据结构课高连生老师布置的作业，没想到在这遇到了，温习一下高老师课件里的思路，如GIF图：

参考题解：
拆解复杂问题：实现一个完整计算器

去掉操作符栈的解法：

    int calculate(String s) {

        Stack<Integer> stk = new Stack<Integer>();

        // 记录算式中的数字
        int num = 0;

        // 记录 num 前的符号，初始化为 +
        char sign = '+';
        
        for (int i = 0; i < s.length(); i++) {

            char c = s.charAt(i);

            // 如果是数字，连续读取到 num
            if (Character.isDigit(c)) {
                num = 10 * num + (c - '0');
            }

            // 如果不是数字，就是遇到了下一个符号，
            // 之前的数字和符号就要存进栈中
            // 防止空格进入 c!=' '
            if ((!Character.isDigit(c) && c!=' ') || i == s.length() - 1) {
                switch (sign) {
                    case '+':
                        stk.push(num);
                        break;
                    case '-':
                        stk.push(-num);
                        break;
                    // 只要拿出前一个数字做对应运算即可
                    case '*':
                        int pre = stk.pop();
                        stk.push(pre * num);
                        break;
                    case '/':
                        pre = stk.pop();
                        stk.push(pre / num);
                        break;
                }
                // 更新符号为当前符号，数字清零
                sign = c;
                num = 0;
            }
        }  //for

        // 将栈中所有结果求和就是答案
        int res = 0;
        while (!stk.empty()) {
            res += stk.pop();
        }
        return res;
    }

这题还可以进阶，加上括号的表达式用回调解，日后再温习一下。

一个小Tips：
注意在switch case语句中第二个pre没有定义，就可以直接使用。
关于这部分的知识点还不熟悉，暂时没找到相关资料，待更新。！！！！！！

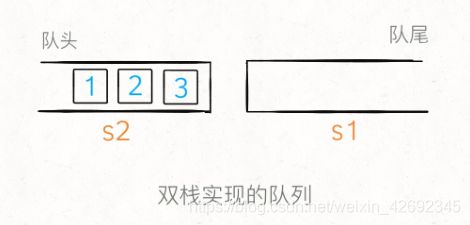
用队列实现栈

执行栈的pop操作时：

import java.util.LinkedList;
import java.util.Queue;

class MyStack {
    Queue<Integer> q = new LinkedList<>();
    int top_elem = 0;

    /** 添加元素到栈顶 */
    public void push(int x) {
        // x 是队列的队尾，是栈的栈顶
        q.offer(x);
        top_elem = x;
    };

    /** 删除栈顶的元素并返回 */
    public int pop() {
        int size = q.size();

        // 把队列前面的都取出来再加入队尾，让之前的队尾元素排到队头
        // 留下队尾 2 个元素, 目的是更新 top_elem 变量
        while (size > 2) {
            q.offer(q.poll());
            size--;
        }

        // 记录新的队尾元素
        top_elem = q.peek();
        q.offer(q.poll());

        // 之前的队尾元素已经到了队头, 删除之前的队尾元素
        return q.poll();
    };

    /** 返回栈顶元素 */
    public int top() {
        return top_elem;
    };

    /** 判断栈是否为空 */
    public boolean empty() {
        return q.isEmpty();
    };
}

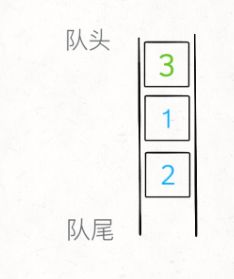
队列（Queue）

实现：
可以借助双链表来实现队列。双链表的头指针允许在队头查看和删除数据，而双链表的尾指针允许我们在队尾查看和添加数据。

循环队列（CircularQueue）

思路：

LeetCode 探索中的小卡片，循环队列的实现：

class MyCircularQueue {
    
    private int[] data;
    private int head;
    private int tail;
    private int size;

    /** Initialize your data structure here. Set the size of the queue to be k. */
    public MyCircularQueue(int k) {
        data = new int[k];
        head = -1;
        tail = -1;
        size = k;
    }
    
    /** Insert an element into the circular queue. Return true if the operation is successful. */
    public boolean enQueue(int value) {
        if (isFull() == true) {
            return false;
        }
        if (isEmpty() == true) {
            head = 0;
        }
        //当空循环队列加入第一个元素时，tail：-1->0
        //这里是抽取出重复代码，没有放在isEmpty的判断中
        tail = (tail + 1) % size;
        data[tail] = value;
        return true;
    }
    
    /** Delete an element from the circular queue. Return true if the operation is successful. */
    public boolean deQueue() {
        if (isEmpty() == true) {
            return false;
        }
        if (head == tail) {
            head = -1;
            tail = -1;
            return true;
        }
        head = (head + 1) % size;
        return true;
    }
    
    /** Get the front item from the queue. */
    public int Front() {
        if (isEmpty() == true) {
            return -1;
        }
        return data[head];
    }
    
    /** Get the last item from the queue. */
    public int Rear() {
        if (isEmpty() == true) {
            return -1;
        }
        return data[tail];
    }
    
    /** Checks whether the circular queue is empty or not. */
    public boolean isEmpty() {
        return head == -1;
    }
    
    /** Checks whether the circular queue is full or not. */
    public boolean isFull() {
        return ((tail + 1) % size) == head;
    }
}

几个重要的点拿出来讲一下：
1.循环队列为空，这时head == -1，tail == -1
2.循环队列满了，这时((tail + 1) % size) == head
3.注意进队和出队的取余操作，再看代码温习一下！

双端队列（Deque）

实现：
与队列相似，可以利用一个双链表实现双端队列。

特点：
双端队列和普通队列最大的不同在于，它允许我们在队列的头尾两端都能在 O(1) 的时间内进行数据的查看、添加和删除。

应用：【动态窗口】

LeetCode 第 239 题：动态滑动窗口

给定一个数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口 k 内的数字，滑动窗口每次只向右移动一位。返回滑动窗口最大值。你可以假设 k 总是有效的，1 ≤ k ≤ 输入数组的大小，且输入数组不为空。

这个题是困难题，可能难点解题用数据结构是双端队列Deque，思路还是按部就班的根据示例找规律code。晒一下代码，注释已经很详细了，思路点击连接。

    public int[] maxSlidingWindow(int[] nums, int k) {
        int nums_length = nums.length;
        if (nums_length <= 1 || k == 1)
            return nums;
        int ans_length = nums_length-k+1;
        int [] ans = new int[ans_length];
        Deque<Integer> deque = new LinkedList<Integer>();
        //indexOfMaxNum用来存储窗口最大值的数组下标
        int indexOfMaxNum = -1;
        for (int i = 0; i < nums_length; i++) {
            //当deque为空, 或者 nums[i] >= 窗口最大值 时
            if (deque.isEmpty() || nums[i] >= nums[indexOfMaxNum]) {
                deque.clear();
                deque.addLast(i);
                indexOfMaxNum = deque.getFirst();
            }
            //当 nums[i] < 窗口最大值 时
            if (!deque.isEmpty() && nums[i] < nums[indexOfMaxNum]) {
                //当i-indexOfMaxNum>=k, 窗口满了, 需要滑动窗口
                if (i-indexOfMaxNum>=k) {
                    deque.removeFirst();
                }
                //循环去除deque中小于nums[i]的元素, 注意!deque.isEmpty()
                while (!deque.isEmpty() && nums[i] > nums[deque.getLast()]) {
                    deque.removeLast();
                }
                deque.addLast(i);
                indexOfMaxNum = deque.getFirst();
            }
            //index 是输出结果数组的坐标, 当循环i=0~k-1时输出的窗口最大值存放在ans[0]中
            int index = i<k ? 0 : i-k+1;
            ans[index] = nums[indexOfMaxNum];
        }
        return ans;
    }

用栈实现队列

import java.util.Stack;

/**
 * 用栈实现队列
 */
public class MyQueue {

    private Stack<Integer> s1, s2;

    public MyQueue() {
        s1 = new Stack<>();
        s2 = new Stack<>();
    }

    /** 添加元素到队尾 */
    public void push(int x) {
        s1.push(x);
    };

    /** 删除队头的元素并返回 */
    public int pop() {
        // 先调用 peek 保证 s2 非空
        peek();
        return s2.pop();
    };

    /** 返回队头元素 */
    public int peek() {
        // 注意: 每次 pop() 或者 peek() 时:
        //      如果s2为空, 则先倒入s1元素, 再从s2取出
        //      如果s2非空, 直接从s2取出
        if (s2.isEmpty())
            // 把 s1 元素压入 s2
            while (!s1.isEmpty())
                s2.push(s1.pop());
        return s2.peek();
    };

    /** 判断队列是否为空 */
    public boolean empty() {
        return s1.isEmpty() && s2.isEmpty();
    };
}

值得⼀提的是，这⼏个操作的时间复杂度是多少呢？有点意思的是 peek 操作，调⽤它时可能触发 while 循环，这样的话时间复杂度是 O(N)，但是⼤部分情况下 while 循环不会被触发，时间复杂度是 O(1)。

由于 pop 操作调⽤了 peek ，它的时间复杂度和 peek 相同。

像这种情况，可以说它们的最坏时间复杂度是 O(N)，因为包含 while 循环，可能需要从 s1 往 s2 搬移元素。

但是它们的均摊时间复杂度是 O(1)，这个要这么理解：对于⼀个元素，最多只可能被搬运⼀次，也就是说 peek 操作平均到每个元素的时间复杂度是 O(1)。

树（Tree）

特点：
递归，也就是说，一棵树要满足某种性质，往往要求每个节点都必须满足。例如，在定义一棵二叉搜索树时，每个节点也都必须是一棵二叉搜索树。

二叉树结点：

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    public TreeNode(int val) {
        this.val = val;
    }
}

下面简单介绍一下几种遍历及其非递归写法。

前序遍历

运用最多的场合包括在树里进行搜索以及创建一棵新的树。

    //二叉树 前序遍历 非递归 根左右
    public void preOrderTraversal(TreeNode root) {
        Stack<TreeNode> stack = new Stack<TreeNode>();
        TreeNode pNode = root;
        while (pNode != null || !stack.isEmpty()) {
            if (pNode != null) {
                System.out.print(pNode.val+", ");
                stack.push(pNode);
                pNode = pNode.left;
            } else { //pNode == null && !stack.isEmpty()
                TreeNode node = stack.pop();
                pNode = node.right;
            }
        }
    }

中序遍历

最常见的是二叉搜索树（BST），由于二叉搜索树的性质就是左孩子小于根节点，根节点小于右孩子，对二叉搜索树进行中序遍历的时候，被访问到的节点大小是按顺序进行的。

    //二叉树 中序遍历 非递归 左根右
    public void inOrderTraversal(TreeNode root) {
        Stack<TreeNode> stack = new Stack<TreeNode>();
        TreeNode pNode = root;
        while (pNode != null || !stack.isEmpty()) {
            if (pNode != null) {
                stack.push(pNode);
                pNode = pNode.left;
            } else { //pNode == null && !stack.isEmpty()
                TreeNode node = stack.pop();
                System.out.print(node.val+", ");
                pNode = node.right;
            }
        }
    }

后序遍历的非递归写法暂时水平有限 有兴趣的读者请自己查阅

层次遍历

    //二叉树 层次遍历
    public void levelOrderTraversal(TreeNode root) {

		if(root==null)  
			return ;  
			
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        TreeNode pNode = root;
        queue.offer(pNode);
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            System.out.print(node.val+", ");
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
    }

LeetCode 第 230 题：第 k 个最小的元素

给定一个二叉搜索树，编写一个函数 kthSmallest 来查找其中第 k 个最小的元素。
这个小破题，中序遍历后第 k-1 个元素即为所求，晒一下非递归写法，值得学习一下。

说明：
你可以假设 k 总是有效的，1 ≤ k ≤ 二叉搜索树元素个数。

示例 1:
输入: root = [3,1,4,null,2], k = 1
   3
  / \
 1   4
  \
   2
输出: 1

示例 2:
输入: root = [5,3,6,2,4,null,null,1], k = 3
       5
      / \
     3   6
    / \
   2   4
  /
 1
输出: 3

public int kthSmallest(TreeNode root, int k) {
	//注意这里Stack用LinkedList实现
	//中序遍历,二叉搜索树,BST,左根右
	LinkedList<TreeNode> stack = new LinkedList<TreeNode>();
	while (true) {
		//所有左子树入栈
		while (root != null) {
			stack.add(root);
			root = root.left;
		}
		//左子树为空,取出根节点
		root = stack.removeLast();
		if (--k == 0) 
			return root.val;
		root = root.right;
	}
}

2020年3月1日看着有点懵 - - 再铺一下本题的递归写法吧

public ArrayList<Integer> inorder(TreeNode root, ArrayList<Integer> arr) {
	if (root == null) return arr;
	inorder(root.left, arr);
	//中序遍历, 左根右, 访问到根时加入List
	arr.add(root.val);
	inorder(root.right, arr);
	return arr;
}

public int kthSmallest(TreeNode root, int k) {
	ArrayList<Integer> nums = inorder(root, new ArrayList<Integer>());
	return nums.get(k - 1);
}

LeetCode 第 104 题：二叉树的最大深度

给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

    3
   / \
  9  20
    /  \
   15   7

返回它的最大深度 3 。

方法一，递归：

public int maxDepth(TreeNode root) {
  if (root == null) {
    return 0;
  } else {
    int left_height = maxDepth(root.left);
    int right_height = maxDepth(root.right);
    return java.lang.Math.max(left_height, right_height) + 1;
  }
}

复杂度分析

• 时间复杂度：我们每个结点只访问一次，因此时间复杂度为 O(N)，其中 N 是结点的数量。
• 空间复杂度：在最糟糕的情况下，树是完全不平衡的，例如每个结点只剩下左子结点，递归将会被调用 N 次（树的高度），因此保持调用栈的存储将是 O(N)。但在最好的情况下（树是完全平衡的），树的高度将是 log(N)。因此，在这种情况下的空间复杂度将是 O(log(N))。

方法二，迭代：
我们还可以在栈的帮助下将上面的递归转换为迭代。

我们的想法是使用 DFS 策略访问每个结点，同时在每次访问时更新最大深度。

所以我们从包含根结点且相应深度为 1 的栈开始。然后我们继续迭代：将当前结点弹出栈并推入子结点。每一步都会更新深度。

import javafx.util.Pair;
import java.lang.Math;

class Solution {
  public int maxDepth(TreeNode root) {
  	//BFS 队列 用于解决最短路径问题
    Queue<Pair<TreeNode, Integer>> queue= new LinkedList<>();
    if (root != null) {
      queue.add(new Pair(root, 1));
    }

	对 广度优先搜索 BFS 的一种改造
    int depth = 0;
    while (!queue.isEmpty()) {
      Pair<TreeNode, Integer> current = queue.poll();
      root = current.getKey();
      int current_depth = current.getValue();
      if (root != null) {
        depth = Math.max(depth, current_depth);
        queue.add(new Pair(root.left, current_depth + 1));
        queue.add(new Pair(root.right, current_depth + 1));
      }
    }
    return depth;
  }
};

LeetCode 第 110 题：平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为：
一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1。

示例 1:
给定二叉树 [3,9,20,null,null,15,7]
    3
   / \
  9  20
    /  \
   15   7
返回 true 。

示例 2:
给定二叉树 [1,2,2,3,3,null,null,4,4]
       1
      / \
     2   2
    / \
   3   3
  / \
 4   4
返回 false 。

参考：力扣官方题解

这个精选题解写的比较好：

110. 平衡二叉树（从底至顶，从顶至底）

思路一：从顶至底（暴力法）

思路是构造一个获取当前节点最大深度的方法 depth(root) ，通过比较此子树的左右子树的最大高度差abs(depth(root.left) - depth(root.right))，来判断此子树是否是二叉平衡树。若树的所有子树都平衡时，此树才平衡。

算法流程：
isBalanced(root) ：判断树 root 是否平衡

• 特例处理： 若树根节点 root 为空，则直接返回 true ；
• 返回值： 所有子树都需要满足平衡树性质，因此以下三者使用与逻辑 && 连接；

1. abs(self.depth(root.left) - self.depth(root.right)) <= 1 ：判断 当前子树 是否是平衡树；
2. self.isBalanced(root.left) ： 先序遍历递归，判断 当前子树的左子树 是否是平衡树；
3. self.isBalanced(root.right) ： 先序遍历递归，判断 当前子树的右子树 是否是平衡树；

depth(root) ： 计算树 root 的最大高度

• 终止条件： 当 root 为空，即越过叶子节点，则返回高度 0 ；
• 返回值： 返回左 / 右子树的最大高度加 1 。

复杂度分析：

• 时间复杂度 O(Nlog2N)： 最差情况下， isBalanced(root) 遍历树所有节点，占用 O(N)；判断每个节点的最大高度 depth(root) 需要遍历各子树的所有节点 ，子树的节点数的复杂度为 O(log2N) 。
• 空间复杂度 O(N)： 最差情况下（树退化为链表时），系统递归需要使用 O(N)的栈空间。

class Solution {
    public boolean isBalanced(TreeNode root) {
        if (root == null) 
        	return true;
        return Math.abs(depth(root.left) - depth(root.right)) <= 1 
        	&& isBalanced(root.left) 
        	&& isBalanced(root.right);
    }

    private int depth(TreeNode root) {
        if (root == null) 
        	return 0;
        return Math.max(depth(root.left), depth(root.right)) + 1;
    }
}

思路二：从底至顶（提前阻断）
思路是对二叉树做先序遍历，从底至顶返回子树最大高度，若判定某子树不是平衡树则 “剪枝” ，直接向上返回。

算法流程：
recur(root):

• 递归返回值：

1. 当节点root 左 / 右子树的高度差 <2 ：则返回以节点root为根节点的子树的最大高度，即节点 root 的左右子树中最大高度加 1 （ max(left, right) + 1 ）；
2. 当节点root 左 / 右子树的高度差 ≥2 ：则返回 −1 ，代表 此子树不是平衡树 。

• 递归终止条件：

1. 当越过叶子节点时，返回高度 0 ；
2. 当左（右）子树高度 left== -1 时，代表此子树的 左（右）子树 不是平衡树，因此直接返回 −1 ；

isBalanced(root) ：

• 返回值： 若 recur(root) != -1 ，则说明此树平衡，返回 true ； 否则返回 false 。

复杂度分析：

• 时间复杂度 O(N)： N 为树的节点数；最差情况下，需要递归遍历树的所有节点。
• 空间复杂度 O(N)： 最差情况下（树退化为链表时），系统递归需要使用 O(N) 的栈空间。

class Solution {
    public boolean isBalanced(TreeNode root) {
        return recur(root) != -1;
    }

    private int recur(TreeNode root) {
        if (root == null) 
        	return 0;
        	
        int left = recur(root.left);
        if(left == -1) 
        	return -1;
        	
        int right = recur(root.right);
        if(right == -1) 
        	return -1;
        	
        return Math.abs(left - right) < 2 ? Math.max(left, right) + 1 : -1;
    }
}