最小生成树 - kruskal 小讲 【 理解 + 例题 】

    最近学不进新的东西，只能看看以前的了，所以！ 今天来看一看kruskal 算法。

    克鲁斯卡尔算法(Kruskal's algorithm)是两个经典的最小生成树算法的较为简单理解的一个。其主要思想就是每次取最小的一条边，直到构成最小生成树。

    假设有n个顶点，那么你需要访问n - 1 条边，其时间复杂度为O（eloge）。Kruskal算法因为只与边相关，适合求稀疏图的最小生成树（即有很少条边或弧的图，稠密图恰反）。而prime算法因为只与顶点有关，适合求稠密图的最小生成树。

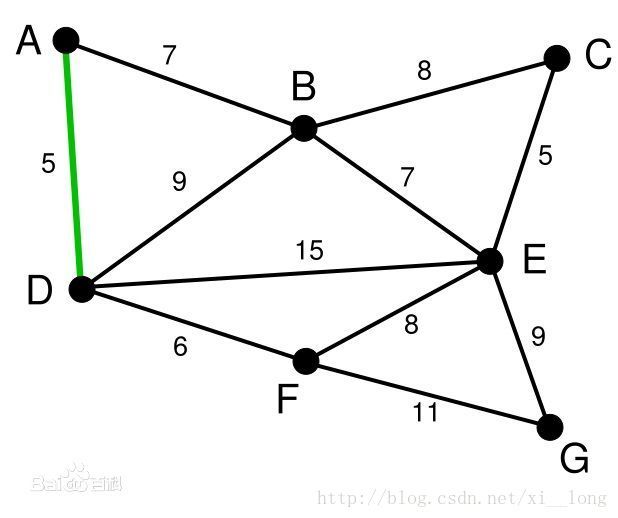
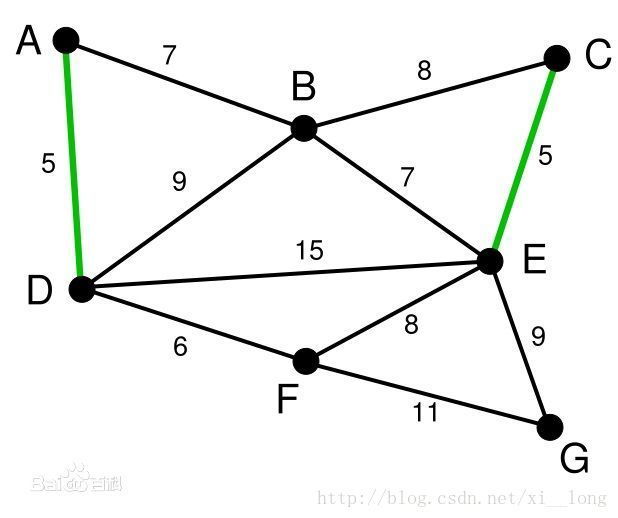
   下面是示意图（图片来自百度百科）

         1.     .                   2                              3               

        4                   5

        看完上面的示意图，可以看来看几道题目了，我觉得，学习一个算法，重要的在于理解，你学的是一种思想，毕竟当比赛或者实际问题的时候，不可能是模版题，所以要去深入地理解，至于使用模版到底好还是不好，我不知道，当你哪一天成为大神的时候，你也许可能会知道，acm这条路，还有很远呢、、、

       再附上一条链接 http://www.wutianqi.com/?p=1284   Tanky Woo 巨巨的

       *  间接排序

        间接排序在这里是一个巧妙的用法 ，不改变原来数组的排列顺序，对数组里面的元素按照一定的顺 序进行排序，在sort 中， 可以这样定义cmp 详解

      

int cmp(const int i, const int j)  //间接排序 ，根据W[i]的大小，排序edge[i],但w[i]的顺序不改变  
{
	return w[i] < w[j];
} 

       HDU   1863   畅通工程     http://acm.hdu.edu.cn/showproblem.php?pid=1863

      此题中还需要注意的是，不一定是一个连通图，所以你得判断是否已经联通了。

#include
#include
#include
using namespace std;

const int N = 1005;
int w[N];
int c[N];
int v[N];
int map[N];//  并查集的时候用到 
int edge[N];// 边 
int n, m;
int i, j;

int cmp(const int i, const int j)  //间接排序 ，根据W[i]的大小，排序edge[i],但w[i]的顺序不改变  
{
	return w[i] < w[j];
} 

int find(int x)
{
    if(x != map[x])
        x = find(map[x]);
    return x;
}

int kruskal()  
{
	int ans = 0;
	int cnt = 0;
	for (i = 0; i < n; i ++)
	{
		edge[i] = i;
	}
	sort(edge, edge + n, cmp);
	for (i = 0; i < m ; i ++)
	{
	    map[i] = i;
	}
	for(i = 0; i < n; i ++)
	{
	    int e = edge[i];
	    int cc = find(c[e]);
	    int vv = find(v[e]);
	    if(cc != vv)
	    {
                map[cc] = vv;
                ans += w[e]; 
                cnt ++;    //计算集合个数，  本体里面如果集合少于m- 1，说明路未齐，输出"?" 
	     }	
	}
	if(cnt < m - 1)
     	ans = 0;
	return ans;
}

int main()
{
	int ans;
	while(~scanf("%d%d",&n, &m))
	{
	    if(n == 0)
		break;
	    for (i = 0; i < n ; i ++)
	    {
		scanf("%d%d%d",&c[i], &v[i], &w[i]);
	    }
	    ans = kruskal();
	    if(ans)
		printf("%d\n",ans);
	    else
		printf("?\n");
	}
	return 0;
}

写完这题  还可以去看看 杭电的畅通系列

    HDU 4463　链接： http://acm.hdu.edu.cn/showproblem.php?pid=4463

    这题也是很基础的最小生成树，只是规定了有两个点，一定要先连一条直线而已，所以照着思路来就可以了，这题尝试了各种方法，所有的最小生成树的方法都用过了，但是还是没有AC，也找不到错在哪里，然后就去看题解了，这种写法是我以前没有见过的，看来水平还是不够的啊、、 下面上代码

#include 
#include 
#include 
#include 
#include 
using namespace std;

struct node
{
    double len;
    int st;
    int ed;
    bool operator <(const node &b) const
    {
        return len < b.len;
    }
}tree[1300];

int fa[60];

int find_m(int x)
{
    if(fa[x]!=x)
    {
        fa[x] = find_m(fa[x]);
        return fa[x];
    }
    return x;
}

int main()
{
    int n,p,q,i,j,k,t,xx,yy;
    double x[60],y[60],sum;
    while(scanf("%d",&n)&&n!=0)
    {
        scanf("%d%d",&p,&q);
        for(i = 1; i <= n; i ++) 
            scanf("%lf%lf",&x[i],&y[i]);
        t = 0;
        for(i = 1;i <=n ;i ++)
        {
            for(j = i + 1; j <= n; j ++)
            {
                tree[t].st = i;
                tree[t].ed = j;
                tree[t].len = sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]));
                t ++;
            }
        }
        for(i = 1;i <= n; i ++)
            fa[i] = i;
        sort(tree,tree + t);
        fa[q] = p;
        int w = 2;
        i = 0;
        sum = sqrt((x[p]-x[q])*(x[p]-x[q])+(y[p]-y[q])*(y[p]-y[q]));
        while(w != n)
        {
            xx = find_m(tree[i].st);
            yy = find_m(tree[i].ed);
            if(xx != yy) 
            {
                fa[yy] = xx;
                w ++;
                sum += tree[i].len;
            }
            i ++;
        }
        printf("%.2f\n",sum);
    }
    return 0;
}