吴恩达深度学习笔记(32)-Dropout正则化Dropout Regularization

dropout 正则化（Dropout Regularization）

除了L2正则化，还有一个非常实用的正则化方法——“Dropout（随机失活）”，我们来看看它的工作原理。

假设你在训练上图这样的神经网络，它存在过拟合，这就是dropout所要处理的，我们复制这个神经网络，dropout会遍历网络的每一层，并设置消除神经网络中节点的概率。假设网络中的每一层，每个节点都以抛硬币的方式设置概率，每个节点得以保留和消除的概率都是0.5，设置完节点概率，我们会消除一些节点，然后删除掉从该节点进出的连线，最后得到一个节点更少，规模更小的网络，然后用backprop方法进行训练。

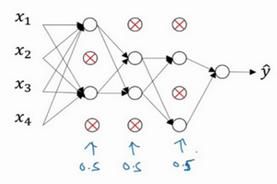
这是网络节点精简后的一个样本，对于其它样本，我们照旧以抛硬币的方式设置概率，保留一类节点集合，删除其它类型的节点集合。对于每个训练样本，我们都将采用一个精简后神经网络来训练它，这种方法似乎有点怪，单纯遍历节点，编码也是随机的，可它真的有效。不过可想而知，我们针对每个训练样本训练规模极小的网络，最后你可能会认识到为什么要正则化网络，因为我们在训练极小的网络。

如何实施dropout呢？

方法有几种，接下来我要讲的是最常用的方法，即inverted dropout（反向随机失活），出于完整性考虑，我们用一个三层（l=3）网络来举例说明。编码中会有很多涉及到3的地方。我只举例说明如何在某一层中实施dropout。

首先要定义向量d，d^([3])表示一个三层的dropout向量：

d3 = np.random.rand(a3.shape[0],a3.shape[1])

然后看它是否小于某数，我们称之为keep-prob，keep-prob是一个具体数字，上个示例中它是0.5，而本例中它是0.8，它表示保留某个隐藏单元的概率，此处keep-prob等于0.8，它意味着消除任意一个隐藏单元的概率是0.2，它的作用就是生成随机矩阵，如果对a^{([3])进行因子分解，效果也是一样的。d}([3])是一个矩阵，每个样本和每个隐藏单元，其中d^([3])中的对应值为1的概率都是0.8，对应为0的概率是0.2，随机数字小于0.8。它等于1的概率是0.8，等于0的概率是0.2。

接下来要做的就是从第三层中获取激活函数，这里我们叫它a^([3])，a([3])含有要计算的激活函数，a^{([3])等于上面的a}([3])乘以d^([3])，a3 =np.multiply(a3,d3)，这里是元素相乘，也可写为a3*=d3，它的作用就是让d^{([3])中所有等于0的元素（输出），而各个元素等于0的概率只有20%，乘法运算最终把d}[3] 中相应元素输出，即让d^{([3])中0元素与a}([3])中相对元素归零。

如果用python实现该算法的话，d^([3])则是一个布尔型数组，值为true和false，而不是1和0，乘法运算依然有效，python会把true和false翻译为1和0，大家可以用python尝试一下。

最后，我们向外扩展a^([3])，用它除以0.8，或者除以keep-prob参数。

a3/=keep-prob

下面我解释一下为什么要这么做，为方便起见，我们假设第三隐藏层上有50个单元或50个神经元，在一维上a^([3])是50，我们通过因子分解将它拆分成50×m维的，保留和删除它们的概率分别为80%和20%，这意味着最后被删除或归零的单元平均有10（50×20%=10）个，

现在我们看下z^([4])，z([4])=w^([4]) a^([3])+b([4])，我们的预期是，a^{([3])减少20%，也就是说a}([3])中有20%的元素被归零，为了不影响z^{([4])的期望值，我们需要用w}([4]) a^{([3])/0.8，它将会修正或弥补我们所需的那20%，a}([3])的期望值不会变，划线部分就是所谓的dropout方法。

它的功能是，不论keep-prop的值是多少0.8，0.9甚至是1，如果keep-prop设置为1，那么就不存在dropout，因为它会保留所有节点。反向随机失活（inverted dropout）方法通过除以keep-prob，确保a^([3])的期望值不变。

事实证明，在测试阶段，当我们评估一个神经网络时，也就是用绿线框标注的反向随机失活方法，使测试阶段变得更容易，因为它的数据扩展问题变少，我们将在下节课讨论。

据我了解，目前实施dropout最常用的方法就是Inverted dropout，建议大家动手实践一下。Dropout早期的迭代版本都没有除以keep-prob，所以在测试阶段，平均值会变得越来越复杂，不过那些版本已经不再使用了。

现在你使用的是d向量，你会发现，不同的训练样本，清除不同的隐藏单元也不同。实际上，如果你通过相同训练集多次传递数据，每次训练数据的梯度不同，则随机对不同隐藏单元归零，有时却并非如此。比如，需要将相同隐藏单元归零，第一次迭代梯度下降时，把一些隐藏单元归零，第二次迭代梯度下降时，也就是第二次遍历训练集时，对不同类型的隐藏层单元归零。向量d或d^([3])用来决定第三层中哪些单元归零，无论用foreprop还是backprop，这里我们只介绍了foreprob。

如何在测试阶段训练算法，在测试阶段，我们已经给出了x，或是想预测的变量，用的是标准计数法。我用a^([0])，第0层的激活函数标注为测试样本x，我们在测试阶段不使用dropout函数，尤其是像下列情况：

z^([1])=w([1]) a^([0])+b([1])

a^([1])=g([1]) (z^([1]))

z^([2])= w^([2]) a^([1])+b([2])

a^([2])=⋯

以此类推直到最后一层，预测值为^y。

显然在测试阶段，我们并未使用dropout，自然也就不用抛硬币来决定失活概率，以及要消除哪些隐藏单元了，因为在测试阶段进行预测时，我们不期望输出结果是随机的，如果测试阶段应用dropout函数，预测会受到干扰。

理论上，你只需要多次运行预测处理过程，每一次，不同的隐藏单元会被随机归零，预测处理遍历它们，但计算效率低，得出的结果也几乎相同，与这个不同程序产生的结果极为相似。

Inverted dropout函数在除以keep-prob时可以记住上一步的操作，目的是确保即使在测试阶段不执行dropout来调整数值范围，激活函数的预期结果也不会发生变化，所以没必要在测试阶段额外添加尺度参数，这与训练阶段不同。

l=keep-prob

为什么dropout会起作用呢？

为什么dropout会起作用呢？下一个笔记我们将更加直观地了解dropout的具体功能。