统计学习方法——逻辑回归和最大熵模型
今天我们介绍两个对数线性模型:逻辑回归和最大熵模型。逻辑回归是一种由条件概率P(Y|X)表示的分类模型,形式为参数化的逻辑斯谛分布。最大熵模型基于最大熵原理,认为学习概率分布模型时,在条件概率不确定的情况下,熵最大的模型即为最好的模型。
逻辑回归
逻辑斯谛分布
在《统计学习方法》这本书中,逻辑斯谛回归模型是目标是最大化条件概率分布P(Y|X),条件概率为参数化的逻辑斯谛分布。所以在介绍逻辑回归前,先来看一下逻辑斯谛分布。设X服从逻辑斯谛分布,其分布函数和密度函数如下:
![]()
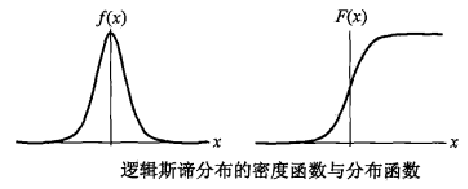
当![]() 时,为标准逻辑斯谛分布。标准逻辑斯谛分布的分布函数和密度函数的图形如图所示:
时,为标准逻辑斯谛分布。标准逻辑斯谛分布的分布函数和密度函数的图形如图所示:
F(x)是以![]() 为中心的中心对称图形。
为中心的中心对称图形。![]() 越小,F(x)在中心附近的梯度越大。对于任意逻辑斯谛分布,有下式成立:
越小,F(x)在中心附近的梯度越大。对于任意逻辑斯谛分布,有下式成立:
了解了逻辑斯谛分布,现在来看看逻辑回归。
逻辑回归
逻辑斯谛回归假设标签Y服从参数p为逻辑斯谛分布的伯努利分布:
其中![]() 表示输入特征;
表示输入特征;![]() 代表标签;
代表标签;![]() 和b为待求参数。对于新的输入数据,我们比较P(Y=1|x)和P(y=0|x)的大小,将实例分到取值大的组内。
和b为待求参数。对于新的输入数据,我们比较P(Y=1|x)和P(y=0|x)的大小,将实例分到取值大的组内。
为了简化后面的计算,令![]() ,
,![]() ,条件概率可以表示为:
,条件概率可以表示为:
![]()
最后通过极大化对数似然函数优化参数:
通过梯度下降法或者拟牛顿法求解最佳参数。
多标签分类任务
逻辑回归只能用于二分类任务中,面对多标签分类任务,我们可以对逻辑回归适当的调整,让它可以解决多分类问题。多标签分类问题有两种:一对一和一对多,即一个数据对应一个标签和一个数据对应多个标签7。
对于一个数据对应一个标签的问题:
将x归入条件概率最大的类别。
对于一个数据对应多个标签的问题,需要对每一类分别训练一个模型,对于每个模型,标签为是k类和非k类,比较![]() 和
和![]() 的大小。若
的大小。若![]() ,则认为x属于第k类。
,则认为x属于第k类。
不过,对比这种讲解方式,我感觉“逻辑回归是在线性回归的基础上,引入sigmoid函数将标签映射到(0,1)区间作为y=1的概率,最后通过最大化对数似然函数求解最佳参数”这种解释方式更容易理解一些。
最大熵模型
最大熵模型是基于最大熵原理提出的,它认为在满足所有鲜艳条件的情况下,熵最大的模型就是最好的模型。最大熵模型为判别式模型,对于给定的输入x,以条件概率P(y|x)输出y。熵的概念在《统计学习方法——决策树》这篇博客中已经介绍过了,我们再稍微复习一下。熵是衡量数据不确定的指标:
![]()
熵的大小和标签取值大小无关,只和每个取值的概率有关;熵越大,数据的不确定性越大,均匀分布数据的熵最大。最大熵模型目标就是在满足所有约束条件的情况下,找出条件熵最大的模型:![]()
我们来举个小例子简单说明一下最大熵模型的思想:一组数据,取值可能为A, B, C, D, E,请问每个取值对应的概率为多少?现在我们只知道它有五个取值,其它的条件一概不知,根据最大熵模型可以认为它们服从均匀分布,及每个取值对应的概率都是1/5;现在我们再引入一个条件P(A)+P(B)=1/3,根据这个条件我们可以知道P(C)+P(D)+P(E)=2/3,但是P(A)、P(B)如何分配这1/3我们不清楚,那我们就认为是均匀分布:P(A)=P(B)=1/6;同理,P(C)=P(D)=P(E)=2/9。
对于给定的训练集![]() ,我们可以确定联合概率分布和先验概率的经验分布:
,我们可以确定联合概率分布和先验概率的经验分布:
![]()
![]()
其中v(X=x, Y=y)表示训练集中X=x, Y=y的样本个数,v(X=x)表示X=x的样本量,N表示总样本量。
特征函数
我们引入特征函数来表示模型的一些约束条件:
这个公式看起来让人有些盲目,我们来看个例子:
这样是不是就很好理解了。我们可以求出基于联合概率分布的特征函数期望值:![]() ,
,
我们希望从数据集里得出的特征函数期望值与基于模型的期望值是相等的,有约束条件:![]()
至此,可以得到我们的优化目标为:
将最大转为最小:
将有约束条件的目标函数转为无约束最优化的对偶函数:
然后求导,令导数为0,进行求解。在求导这里,参考一些其他博客,个人认为《统计学习方法》里求导这里可能存在一些错误,我认为这里的求导应该是对p(Y=y|X=x)求的,这里的y和x都是指定的值,而非X和Y可以取的任意值,所以在求导过程中对于左边第一个求和项,只有{X=x,Y=y}对应的式子求导结果不为0,即:
所以在L(p,w)对p求导结果为:
由于![]() ,有
,有
求出p(y|x),接下来通过优化算法(迭代尺度法、牛顿法、拟牛顿法...)就是求出![]() 就欧克了。
就欧克了。
参考:
https://blog.csdn.net/yutao03081/article/details/78812014 特征函数的例子就是参考这篇伯克利
https://www.cnblogs.com/hexinuaa/p/3353479.html,这个博客的最大熵模型讲的非常详细,值得学习。
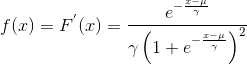
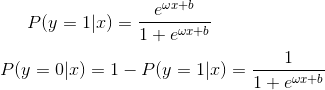
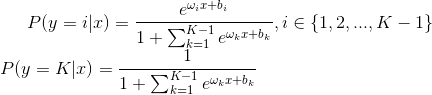


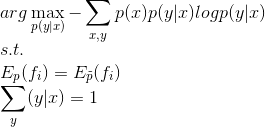
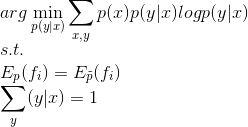
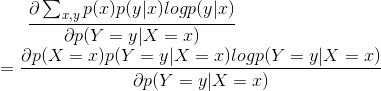
![\frac{\partial L}{\partial p}\\ =\tilde{p}(X=x)\left [logp(Y=y|X=x)+1 \right ]-\omega_0-\sum_{i=1}^{n}\omega_if_i\tilde{p}(X=x)\\](http://img.e-com-net.com/image/info8/2a4fe5bd66f546b5b81d11ea1f395b77.gif)