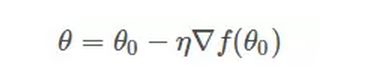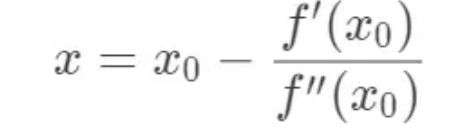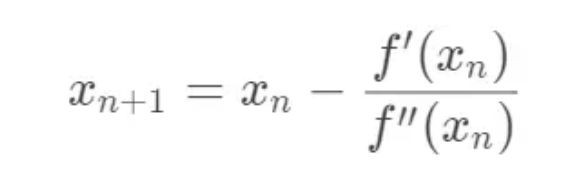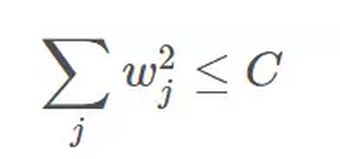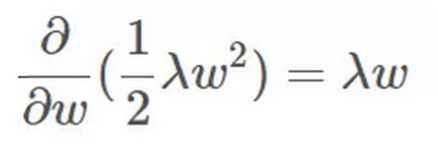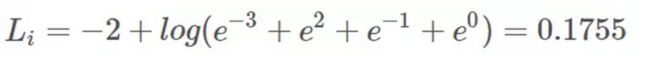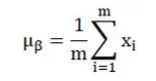梯度下降、牛顿法凸优化、L1、L2正则化、softmax、Batchnorm、droupout、Targeted Dropout详解

一、梯度下降

问题提出：虽然给定一个假设函数，我们能够根据cost function知道这个假设函数拟合的好不好，但是毕竟函数有这么多，总不可能一个一个试吧？因此我们引出了梯度下降：能够找出cost function函数的最小值；

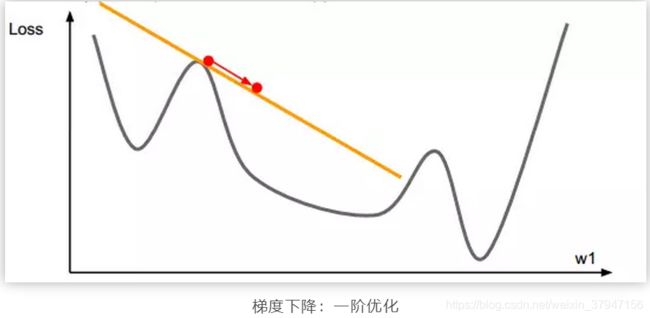
梯度下降背后的思想是：开始时我们随机选择一个参数的组合（θ0,θ1,...,θn），计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到到到一个局部最小值（local minimum）。直白的话说，梯度下降原理：将函数比作一座山，我们站在某个山坡上，往四周看，从哪个方向向下走一小步，能够下降的最快。如图所示。

下山问题

假设我们位于黄山的某个山腰处，山势连绵不绝，不知道怎么下山。于是决定走一步算一步，也就是每次沿着当前位置最陡峭最易下山的方向前进一小步，然后继续沿下一个位置最陡方向前进一小步。这样一步一步走下去，一直走到觉得我们已经到了山脚。这里的下山最陡的方向就是梯度的负方向。

首先理解什么是梯度？通俗来说，梯度就是表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在当前位置的导数。

上式中，θ是自变量，f(θ)是关于θ的函数，θ表示梯度。

 

如果函数f(θ)是凸函数，那么就可以使用梯度下降算法进行优化。梯度下降算法的公式我们已经很熟悉了：

其中，θo是自变量参数，即下山位置坐标，η是学习因子，即下山每次前进的一小步（步进长度），θ是更新后的θo，即下山移动一小步之后的位置。

一阶泰勒展开式

这里需要一点数学基础，对泰勒展开式有些了解。简单地来说，一阶泰勒展开式利用的就是函数的局部线性近似这个概念。我们以一阶泰勒展开式为例：

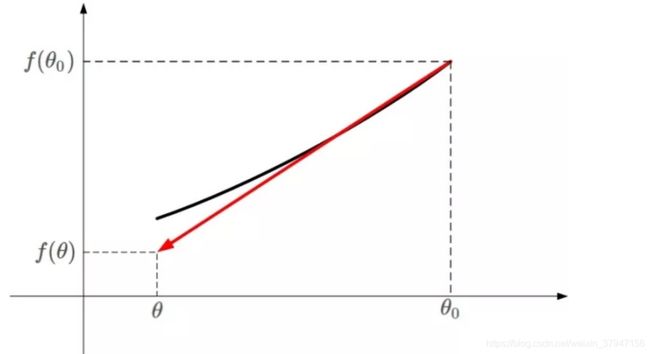
不懂上面的公式？没有关系。我用下面这张图来解释。

凸函数f(θ)的某一小段[θo,θ]由上图黑色曲线表示，可以利用线性近似的思想求出f(θ)的值，如上图红色直线。该直线的斜率等于f(θ)在θo处的导数。则根据直线方程，很容易得到f(θ)的近似表达式为：

这就是一阶泰勒展开式的推导过程，主要利用的数学思想就是曲线函数的线性拟合近似。

梯度下降数学原理

知道了一阶泰勒展开式之后，接下来就是重点了！我们来看一下梯度下降算法是如何推导的。

 

先写出一阶泰勒展开式的表达式：

其中，θ−θo是微小矢量，它的大小就是我们之前讲的步进长度η，类比于下山过程中每次前进的一小步，η为标量，而θ−θo的单位向量用v表示。则θ−θo可表示为：

特别需要注意的是，θ−θo不能太大，因为太大的话，线性近似就不够准确，一阶泰勒近似也不成立了。替换之后，f(θ)的表达式为：

重点来了，局部下降的目的是希望每次θ更新，都能让函数值f(θ)变小。也就是说，上式中，我们希望f(θ)。则有：

因为η为标量，且一般设定为正值，所以可以忽略，不等式变成了：

上面这个不等式非常重要！v和∇f(θo)都是向量，∇f(θo)是当前位置的梯度方向，v表示下一步前进的单位向量，是需要我们求解的，有了它，就能根据vθ−θo=ηv确定θ值了。

 

想要两个向量的乘积小于零，我们先来看一下两个向量乘积包含哪几种情况：

A和B均为向量，α为两个向量之间的夹角。A和B的乘积为：

||A||和||B||均为标量，在||A||和||B||确定的情况下，只要cos(α)=−1，即A和B完全反向，就能让A和B的向量乘积最小（负最大值）。

 

顾名思义，当v与∇f(θo)互为反向，即v为当前梯度方向的负方向的时候，能让v⋅∇f(θo)最大程度地小，也就保证了v的方向是局部下降最快的方向。

 

知道v是∇f(θo)的反方向后，可直接得到：

之所以要除以∇f(θo)的模||∇f(θo)||，是因为v是单位向量。

 

求出最优解v之后，带入到θ−θo=ηv中，得：

一般地，因为||∇f(θo)||是标量，可以并入到步进因子η中，即简化为：

这样，我们就推导得到了梯度下降算法中θ的更新表达式。

二、牛顿法凸优化

1、牛顿法求解方程的根

 

有时候，在方程比较复杂的情况下，使用一般方法求解它的根并不容易。牛顿法通过迭代的方式和不断逼近的思想，可以近似求得方程较为准确的根。

 

牛顿法求根的核心思想是泰勒一阶展开。例如对于方程 f(x) = 0，我们在任意一点 x0 处，进行一阶泰勒展开：

令 f(x) = 0，带入上式，即可得到：

注意，这里使用了近似，得到的 x 并不是方程的根，只是近似解。但是，x 比 x0 更接近于方程的根。效果如下图所示：

 

 

然后，利用迭代方法求解，以 x 为 x0，求解下一个距离方程的根更近的位置。迭代公式可以写成：

经过一定次数的有效迭代后，一般都能保证在方程的根处收敛。下面给出整个迭代收敛过程的动态演示。

 

 

2、牛顿法凸优化

上一部分介绍牛顿法如何求解方程的根，这一特性可以应用在凸函数的优化问题上。

机器学习、深度学习中，损失函数的优化问题一般是基于一阶导数梯度下降的。现在，从另一个角度来看，想要让损失函数最小化，这其实是一个最值问题，对应函数的一阶导数 f'(x) = 0。也就是说，如果我们找到了能让 f'(x) = 0 的点 x，损失函数取得最小值，也就实现了模型优化目标。

现在的目标是计算 f'(x) = 0 对应的 x，即 f'(x) = 0 的根。转化为求根问题，就可以利用上一节的牛顿法了。

与上一节有所不同，首先，对 f(x) 在 x0 处进行二阶泰勒展开：

上式成立的条件是 f(x) 近似等于 f(x0)。令 f(x) = f(x0)，并对 (x - x0) 求导，可得：

同样，虽然 x 并不是最优解点，但是 x 比 x0 更接近 f'(x) = 0 的根。这样，就能得到最优化的迭代公式：

通过迭代公式，就能不断地找到 f'(x) = 0 的近似根，从而也就实现了损失函数最小化的优化目标。

3、梯度下降 VS 牛顿法

现在，分别写出梯度下降和牛顿法的更新公式：

 

梯度下降算法是将函数在 xn 位置进行一次函数近似，也就是一条直线。计算梯度，从而决定下一步优化的方向是梯度的反方向。而牛顿法是将函数在 xn 位置进行二阶函数近似，也就是二次曲线。计算梯度和二阶导数，从而决定下一步的优化方向。一阶优化和二阶优化的示意图如下所示：

 

 

 

以上所说的是梯度下降和牛顿法的优化方式差异。那么谁的优化效果更好呢？

于牛顿法和梯度下降法的效率对比：

　　从本质上去看，牛顿法是二阶收敛，梯度下降是一阶收敛，所以牛顿法就更快。如果更通俗地说的话，比如你想找一条最短的路径走到一个盆地的最底部，梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。（牛顿法目光更加长远，所以少走弯路；相对而言，梯度下降法只考虑了局部的最优，没有全局思想。）

　　根据wiki上的解释，从几何上说，牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面，而梯度下降法是用一个平面去拟合当前的局部曲面，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。

注：红色的牛顿法的迭代路径，绿色的是梯度下降法的迭代路径。

牛顿法的优缺点总结：

　　优点：二阶收敛，收敛速度快；

　　缺点：牛顿法是一种迭代算法，每一步都需要求解目标函数的Hessian矩阵的逆矩阵，计算比较复杂。

 

然后，我们再来看一下牛顿法的缺点。我们注意到牛顿法迭代公式中除了需要求解一阶导数之外，还要计算二阶导数。从矩阵的角度来说，一阶导数和二阶导数分别对应雅可比矩阵（Jacobian matrix）和海森矩阵（Hessian matrix）

牛顿法不仅需要计算 Hessian 矩阵，而且需要计算 Hessian 矩阵的逆。当数据量比较少的时候，运算速度不会受到大的影响。但是，当数据量很大，特别在深度神经网络中，计算 Hessian 矩阵和它的逆矩阵是非常耗时的。从整体效果来看，牛顿法优化速度没有梯度下降算法那么快。所以，目前神经网络损失函数的优化策略大多都是基于梯度下降。

值得一提的是，针对牛顿法的缺点，目前已经有一些改进算法。这类改进算法统称拟牛顿算法。比较有代表性的是 BFGS 和 L-BFGS。 可以参考：http://www.cnblogs.com/liuwu265/p/4714396.html

三、 L1 和 L2 正则化

1、L2 正则化直观解释

L2 正则化公式非常简单，直接在原来的损失函数基础上加上权重参数的平方和：

 

 

其中，Ein 是未包含正则化项的训练样本误差，λ 是正则化参数，可调。但是正则化项是如何推导的？接下来，我将详细介绍其中的物理意义。

我们知道，正则化的目的是限制参数过多或者过大，避免模型更加复杂。例如，使用多项式模型，如果使用 10 阶多项式，模型可能过于复杂，容易发生过拟合。所以，为了防止过拟合，我们可以将其高阶部分的权重 w 限制为 0，这样，就相当于从高阶的形式转换为低阶。

为了达到这一目的，最直观的方法就是限制 w 的个数，但是这类条件属于 NP-hard 问题，求解非常困难。所以，一般的做法是寻找更宽松的限定条件：

 

 

上式是对 w 的平方和做数值上界限定，即所有w 的平方和不超过参数 C。这时候，我们的目标就转换为：最小化训练样本误差 Ein，但是要遵循 w 平方和小于 C 的条件。

下面，我用一张图来说明如何在限定条件下，对 Ein 进行最小化的优化。

如上图所示，蓝色椭是最小化 Ein 区域，红色圆圈是 w 的限定条件区域。在没有限定条件的情况下，一般使用梯度下降算法，在蓝色椭圆区域内会一直沿着 w 梯度的反方向前进，直到找到全局最优值 wlin。例如空间中有一点 w（图中紫色点），此时 w 会沿着 -∇Ein 的方向移动，如图中蓝色箭头所示。但是，由于存在限定条件，w 不能离开红色圆形区域，最多只能位于圆上边缘位置，沿着切线方向。w 的方向如图中红色箭头所示。

那么问题来了，存在限定条件，w 最终会在什么位置取得最优解呢？也就是说在满足限定条件的基础上，尽量让 Ein 最小。

我们来看，w 是沿着圆的切线方向运动，如上图绿色箭头所示。运动方向与 w 的方向（红色箭头方向）垂直。运动过程中，根据向量知识，只要 -∇Ein 与运行方向有夹角，不垂直，则表明 -∇Ein 仍会在 w 切线方向上产生分量，那么 w 就会继续运动，寻找下一步最优解。只有当 -∇Ein 与 w 的切线方向垂直时，-∇Ein在 w 的切线方向才没有分量，这时候 w 才会停止更新，到达最接近 wlin 的位置，且同时满足限定条件。

 

 

-∇Ein 与 w 的切线方向垂直，即 -∇Ein 与 w 的方向平行。如上图所示，蓝色箭头和红色箭头互相平行。这样，根据平行关系得到：

 

 

移项，得：

 

 

这样，我们就把优化目标和限定条件整合在一个式子中了。也就是说只要在优化 Ein 的过程中满足上式，就能实现正则化目标。

 

接下来，重点来了！根据最优化算法的思想：梯度为 0 的时候，函数取得最优值。已知 ∇Ein 是 Ein 的梯度，观察上式，λw 是否也能看成是某个表达式的梯度呢？

 

当然可以！λw 可以看成是 1/2λw*w 的梯度：

 

 

这样，我们根据平行关系求得的公式，构造一个新的损失函数：

 

 

之所以这样定义，是因为对 Eaug 求导，正好得到上面所求的平行关系式。上式中等式右边第二项就是 L2 正则化项。

 

这样， 我们从图像化的角度，分析了 L2 正则化的物理意义，解释了带 L2 正则化项的损失函数是如何推导而来的。

 

2、L1 正则化直观解释

 

L1 正则化公式也很简单，直接在原来的损失函数基础上加上权重参数的绝对值：

 

 

我仍然用一张图来说明如何在 L1 正则化下，对 Ein 进行最小化的优化。

 

 

Ein 优化算法不变，L1 正则化限定了 w 的有效区域是一个正方形，且满足 |w| < C。空间中的点 w 沿着 -∇Ein 的方向移动。但是，w 不能离开红色正方形区域，最多只能位于正方形边缘位置。其推导过程与 L2 类似，此处不再赘述。

 

3、L1 与 L2 解的稀疏性

 

介绍完 L1 和 L2 正则化的物理解释和数学推导之后，我们再来看看它们解的分布性。

 

以二维情况讨论，上图左边是 L2 正则化，右边是 L1 正则化。从另一个方面来看，满足正则化条件，实际上是求解蓝色区域与黄色区域的交点，即同时满足限定条件和 Ein 最小化。对于 L2 来说，限定区域是圆，这样，得到的解 w1 或 w2 为 0 的概率很小，很大概率是非零的。

 

对于 L1 来说，限定区域是正方形，方形与蓝色区域相交的交点是顶点的概率很大，这从视觉和常识上来看是很容易理解的。也就是说，方形的凸点会更接近 Ein 最优解对应的 wlin 位置，而凸点处必有 w1 或 w2 为 0。这样，得到的解 w1 或 w2 为零的概率就很大了。所以，L1 正则化的解具有稀疏性。

 

扩展到高维，同样的道理，L2 的限定区域是平滑的，与中心点等距；而 L1 的限定区域是包含凸点的，尖锐的。这些凸点更接近 Ein 的最优解位置，而在这些凸点上，很多 wj 为 0。

关于 L1 更容易得到稀疏解的原因，有一个很棒的解释，请见下面的链接：

https://www.zhihu.com/question/37096933/answer/70507353

 

4、正则化参数 λ

 

正则化是结构风险最小化的一种策略实现，能够有效降低过拟合。损失函数实际上包含了两个方面：一个是训练样本误差。一个是正则化项。其中，参数 λ 起到了权衡的作用。

 

以 L2 为例，若 λ 很小，对应上文中的 C 值就很大。这时候，圆形区域很大，能够让 w 更接近 Ein 最优解的位置。若 λ 近似为 0，相当于圆形区域覆盖了最优解位置，这时候，正则化失效，容易造成过拟合。相反，若 λ 很大，对应上文中的 C 值就很小。这时候，圆形区域很小，w 离 Ein 最优解的位置较远。w 被限制在一个很小的区域内变化，w 普遍较小且接近 0，起到了正则化的效果。但是，λ 过大容易造成欠拟合。欠拟合和过拟合是两种对立的状态。

四、softmax

1、什么是Softmax？

 

Softmax 在机器学习和深度学习中有着非常广泛的应用。尤其在处理多分类（C > 2）问题，分类器最后的输出单元需要Softmax 函数进行数值处理。关于Softmax 函数的定义如下所示：

 

 

其中，Vi 是分类器前级输出单元的输出。i 表示类别索引，总的类别个数为 C。Si 表示的是当前元素的指数与所有元素指数和的比值。Softmax 将多分类的输出数值转化为相对概率，更容易理解和比较。我们来看下面这个例子。

 

一个多分类问题，C = 4。线性分类器模型最后输出层包含了四个输出值，分别是：

 

 

经过Softmax处理后，数值转化为相对概率：

 

 

很明显，Softmax 的输出表征了不同类别之间的相对概率。我们可以清晰地看出，S1 = 0.8390，对应的概率最大，则更清晰地可以判断预测为第1类的可能性更大。Softmax 将连续数值转化成相对概率，更有利于我们理解。

 

实际应用中，使用 Softmax 需要注意数值溢出的问题。因为有指数运算，如果 V 数值很大，经过指数运算后的数值往往可能有溢出的可能。所以，需要对 V 进行一些数值处理：即 V 中的每个元素减去 V 中的最大值。

 

 

2、Softmax 损失函数

 

我们知道，线性分类器的输出是输入 x 与权重系数的矩阵相乘：s = Wx。对于多分类问题，使用 Softmax 对线性输出进行处理。这一小节我们来探讨下 Softmax 的损失函数。

 

 

其中，Syi是正确类别对应的线性得分函数，Si 是正确类别对应的 Softmax输出。

 

由于 log 运算符不会影响函数的单调性，我们对 Si 进行 log 操作：

 

我们希望 Si 越大越好，即正确类别对应的相对概率越大越好，那么就可以对 Si 前面加个负号，来表示损失函数：

 

 

对上式进一步处理，把指数约去：

 

 

这样，Softmax 的损失函数就转换成了简单的形式。

 

举个简单的例子，上一小节中得到的线性输出为：

 

 

假设 i = 1 为真实样本，计算其损失函数为：

 

若令 i = 0 为真实样本，计算其损失函数为：

 

 

 

3、Softmax 反向梯度

 

推导了 Softmax 的损失函数之后，接下来继续对权重参数进行反向求导。

 

Softmax 线性分类器中，线性输出为：

 

 

其中，下标 i 表示第 i 个样本。

 

求导过程的程序设计直接使用矩阵运算。

使用矩阵运算，对权重 W 求导函数定义如下：

 

def softmax_loss_vectorized(W, X, y, reg):
 """
 Softmax loss function, vectorized version.

 Inputs and outputs are the same as softmax_loss_naive.
 """
 # Initialize the loss and gradient to zero.
 loss = 0.0
 dW = np.zeros_like(W)

 num_train = X.shape[0]
 num_classes = W.shape[1]
 scores = X.dot(W)
 scores_shift = scores - np.max(scores, axis = 1).reshape(-1,1)
 softmax_output = np.exp(scores_shift) / np.sum(np.exp(scores_shift), axis=1).reshape(-1,1)
 loss = -np.sum(np.log(softmax_output[range(num_train), list(y)]))
 loss /= num_train
 loss += 0.5 * reg * np.sum(W * W)

 dS = softmax_output.copy()
 dS[range(num_train), list(y)] += -1
 dW = (X.T).dot(dS)
 dW = dW / num_train + reg * W  

 return loss, dW

 

4、Softmax 与 SVM 

 

Softmax线性分类器的损失函数计算相对概率，又称交叉熵损失「Cross Entropy Loss」。线性 SVM 分类器和 Softmax 线性分类器的主要区别在于损失函数不同。SVM 使用 hinge loss，更关注分类正确样本和错误样本之间的距离「Δ = 1」，只要距离大于 Δ，就不在乎到底距离相差多少，忽略细节。而 Softmax 中每个类别的得分函数都会影响其损失函数的大小。举个例子来说明，类别个数 C = 3，两个样本的得分函数分别为[10, -10, -10]，[10, 9, 9]，真实标签为第0类。对于 SVM 来说，这两个 Li 都为0；但对于Softmax来说，这两个 Li 分别为0.00和0.55，差别很大。

五、Batchnorm

1、Batchnorm 原理解读

为了减小Internal Covariate Shift，对神经网络的每一层做归一化不就可以了，假设将每一层输出后的数据都归一化到0均值，1方差，满足正太分布，但是，此时有一个问题，每一层的数据分布都是标准正太分布，导致其完全学习不到输入数据的特征，因为，费劲心思学习到的特征分布被归一化了，因此，直接对每一层做归一化显然是不合理的。

但是如果稍作修改，加入可训练的参数做归一化，那就是BatchNorm实现的了，接下来结合下图的伪代码做详细的分析： 

之所以称之为batchnorm是因为所norm的数据是一个batch的，假设输入数据是β=x_(1...m)共m个数据，输出是y_i=BN(x)，batchnorm的步骤如下：

1. 先求出此次批量数据x的均值

   

2. 求出此次batch的方差

   

3. 接下来就是对x做归一化，得到x_i^-

4. 最重要的一步，引入缩放和平移变量γ和β，计算归一化后的值

   

 

接下来详细介绍一下这额外的两个参数，之前也说过如果直接做归一化不做其他处理，神经网络是学不到任何东西的，但是加入这两个参数后，事情就不一样了，先考虑特殊情况下，如果γ和β分别等于此batch的方差和均值，那么y_i不就还原到归一化前的x了吗，也即是缩放平移到了归一化前的分布，相当于batchnorm没有起作用，γ和β分别称之为 平移参数和缩放参数 。这样就保证了每一次数据经过归一化后还保留的有学习来的特征，同时又能完成归一化这个操作，加速训练。

 

先用一个简单的代码举个小栗子：

def Batchnorm_simple_for_train(x, gamma,beta, bn_param):"""
param:x   : 输入数据，设shape(B,L)
param:gama : 缩放因子  γ
param:beta : 平移因子  β
param:bn_param   : batchnorm所需要的一些参数
   eps      : 接近0的数，防止分母出现0
   momentum : 动量参数，一般为0.9，0.99， 0.999
   running_mean ：滑动平均的方式计算新的均值，训练时计算，为测试数据做准备
   running_var  : 滑动平均的方式计算新的方差，训练时计算，为测试数据做准备
"""
   running_mean = bn_param['running_mean'] #shape = [B]
   running_var = bn_param['running_var']   #shape = [B]
   results = 0. # 建立一个新的变量
   x_mean=x.mean(axis=0)  # 计算x的均值
   x_var=x.var(axis=0)    # 计算方差
   x_normalized=(x-x_mean)/np.sqrt(x_var+eps)       # 归一化
   results = gamma * x_normalized + beta            # 缩放平移
   running_mean = momentum * running_mean + (1 - momentum) * x_mean
   running_var = momentum * running_var + (1 - momentum) * x_var    #记录新的值
   bn_param['running_mean'] = running_mean
   bn_param['running_var'] = running_var   return results , bn_param

看完这个代码是不是对batchnorm有了一个清晰的理解，首先计算均值和方差，然后归一化，然后缩放和平移，完事！但是这是在训练中完成的任务，每次训练给一个批量，然后计算批量的均值方差，但是在测试的时候可不是这样，测试的时候每次只输入一张图片，这怎么计算批量的均值和方差，于是，就有了代码中下面两行，在训练的时候实现计算好mean var测试的时候直接拿来用就可以了，不用计算均值和方差。

running_mean = momentum * running_mean + (1- momentum) * x_mean
running_var = momentum * running_var + (1 -momentum) * x_var

所以，测试的时候是这样的：

def Batchnorm_simple_for_test(x, gamma,beta, bn_param):"""
param:x   : 输入数据，设shape(B,L)
param:gama : 缩放因子  γ
param:beta : 平移因子  β
param:bn_param   : batchnorm所需要的一些参数
   eps      : 接近0的数，防止分母出现0
   momentum : 动量参数，一般为0.9，0.99， 0.999
   running_mean ：滑动平均的方式计算新的均值，训练时计算，为测试数据做准备
   running_var  : 滑动平均的方式计算新的方差，训练时计算，为测试数据做准备
"""
   running_mean = bn_param['running_mean'] #shape = [B]
   running_var = bn_param['running_var']   #shape = [B]
   results = 0. # 建立一个新的变量
   x_normalized=(x-running_mean )/np.sqrt(running_var +eps)       # 归一化
   results = gamma * x_normalized + beta            # 缩放平移
   return results , bn_param

你是否理解了呢？如果还没有理解的话，欢迎再多看几遍。

2、Batchnorm源码解读

本节主要讲解一段tensorflow中Batchnorm的可以使用的代码，如下： 

代码来自知乎，这里加入注释帮助阅读。

def batch_norm_layer(x, train_phase,scope_bn):
   with tf.variable_scope(scope_bn):
        # 新建两个变量，平移、缩放因子
       beta = tf.Variable(tf.constant(0.0, shape=[x.shape[-1]]), name='beta',trainable=True)
       gamma = tf.Variable(tf.constant(1.0, shape=[x.shape[-1]]), name='gamma',trainable=True)
       # 计算此次批量的均值和方差
       axises = np.arange(len(x.shape) - 1)
       batch_mean, batch_var = tf.nn.moments(x, axises, name='moments')
       # 滑动平均做衰减
       ema = tf.train.ExponentialMovingAverage(decay=0.5)
       def mean_var_with_update():
           ema_apply_op = ema.apply([batch_mean, batch_var])
           with tf.control_dependencies([ema_apply_op]):
                return tf.identity(batch_mean),tf.identity(batch_var)
       # train_phase 训练还是测试的flag
       # 训练阶段计算runing_mean和runing_var，使用mean_var_with_update（）函数
       # 测试的时候直接把之前计算的拿去用 ema.average(batch_mean)
       mean, var = tf.cond(train_phase, mean_var_with_update,
                            lambda:(ema.average(batch_mean), ema.average(batch_var)))
       normed = tf.nn.batch_normalization(x, mean, var, beta, gamma, 1e-3)
   return normed

至于此行代码tf.nn.batch_normalization()就是简单的计算batchnorm过程啦，代码如下： 

这个函数所实现的功能就如此公式：

def batch_normalization(x, mean, variance, offset,scale, variance_epsilon, name=None):
   with ops.name_scope(name, "batchnorm", [x, mean, variance,scale, offset]):
       inv = math_ops.rsqrt(variance + variance_epsilon)
    if scale is not None:
           inv *= scale      
       return x * inv + (offset - mean * inv
                       if offset is not Noneelse -mean * inv)

3、Batchnorm的优点及缺点

主要部分说完了，接下来对BatchNorm做一个总结：

1. 没有它之前，需要小心的调整学习率和权重初始化，但是有了BN可以放心的使用大学习率，但是使用了BN，就不用小心的调参了，较大的学习率极大的提高了学习速度，

2. Batchnorm本身上也是一种正则的方式，可以代替其他正则方式如dropout等

3. 另外，个人认为，batchnorm降低了数据之间的绝对差异，有一个去相关的性质，更多的考虑相对差异性，因此在分类任务上具有更好的效果

六、droupout

Dropout是指在模型训练时随机让网络某些隐含层节点的权重不工作，不工作的那些节点可以暂时认为不是网络结构的一部分，但是它的权重得保留下来（只是暂时不更新而已），因为下次样本输入时它可能又得工作了。训练神经网络模型时，如果训练样本较少，为了防止模型过拟合，Dropout可以作为一种trikc供选择。

 

关于Dropout，文章中没有给出任何数学解释，Hintion的直观解释和理由如下：

　　1. 由于每次用输入网络的样本进行权值更新时，隐含节点都是以一定概率随机出现，因此不能保证每2个隐含节点每次都同时出现，这样权值的更新不再依赖于有固定关系隐含节点的共同作用，阻止了某些特征仅仅在其它特定特征下才有效果的情况。

　　2. 可以将dropout看作是模型平均的一种。对于每次输入到网络中的样本（可能是一个样本，也可能是一个batch的样本），其对应的网络结构都是不同的，但所有的这些不同的网络结构又同时share隐含节点的权值。这样不同的样本就对应不同的模型，是bagging的一种极端情况。个人感觉这个解释稍微靠谱些，和bagging，boosting理论有点像，但又不完全相同。（关于bagging 和 boosting 后边会简单学习并介绍，之前了解但是不理解）

　　3. native bayes是dropout的一个特例。Native bayes有个错误的前提，即假设各个特征之间相互独立，这样在训练样本比较少的情况下，单独对每个特征进行学习，测试时将所有的特征都相乘，且在实际应用时效果还不错。而Droput每次不是训练一个特征，而是一部分隐含层特征。

　　4. 还有一个比较有意思的解释是，Dropout类似于性别在生物进化中的角色，物种为了使适应不断变化的环境，性别的出现有效的阻止了过拟合，即避免环境改变时物种可能面临的灭亡。

更直观个人理解就是： droput 取50%的时候，每次训练都随机的discard 50%的隐含层的节点来进行训练，这样可以防止每次都是所有的特征选择器共同作用，一直放大或者缩小某些特征，在样本数据少的情况下很容易过拟合，并且泛化能力也很弱，所以才用dropout这种方法来实现能很好的避免训练过程中出现的这些问题。注意，在测试过程中采用的是全连接。

七、Targeted Dropout。

 

神经网络是一种非常灵活的模型，由于其参数众多，有利于学习，但也具有高度的冗余性。这使得在不影响性能的情况下压缩神经网络成为可能。

我们引入了有针对性的Targeted Dropout，这是一种对神经网络权重和单元进行剪枝的策略，它将剪枝机制直接引入到学习中。在每次权值更新时，Targeted Dropout使用一个简单的选择标准选择一个候选组进行剪枝，然后通过应用于该集合的dropout对网络进行随机剪枝。与更复杂的正则化方案相比，最终的网络学会了更鲁棒的剪枝，同时具有极其简单的实现和易于调整的特性。

?基础知识?

D r o p o u t

本次研究工作主要使用了两种最流行的Bernoulli Dropout技术，Hinton等人的Unit Dropout[1,2]和wan等人的Weight Dropout[3]。对于具有输入张量X、权重矩阵W、输出张量Y和Mask M的全连接层，定义了以下两种技术：

Unit Dropout：

Unit Dropout随机drop unit(有时称为神经元)在每个训练步骤，以减少unit之间的依赖，防止过拟合。

Weight Dropout：

在每个训练步骤中，Weight Dropout都会随机drop权重矩阵中的单个权重。直观地说，这是层间的dropping connection，迫使网络适应不同的连接在每一个训练步骤。

✂️Magnitude-based pruning✂️

一种流行的剪枝策略是那些Magnitude-based的剪枝策略。这些策略将Top-k的最大Magnitude权重视为重要因素，使用arg max-k返回所有考虑的元素中的Top-k元素(单位或权重)。

Unit Dropout：

考虑在L2范数下权矩阵的unit(列向量)：

Weight Dropout：

在L1-范数下分别考虑权重矩阵的每一项。请注意，top-k相对于相同滤波器中的其他权重：

虽然weight剪枝倾向于在更粗的剪枝下保持更多的任务性能，但unit剪枝可以大大节省计算量。

⚠️ 方法 ⚠️

考虑一个由θ参数化的神经网络，且希望按照Unit Dropout和Weight Dropout定义的方法对W进行剪枝。

因此，希望找到最优参数θ*，它能令损失函数ε(W(θ*))尽可能小的同时，令|W(θ* )|≤k，即希望保留神经网络中最高数量级的k个权重。一个确定性的实现可以选择最小的|θ|−k个元素，并删除它们。但是如果这些较小的值在训练中变得更重要，那么它们的数值应该是增加的。因此，通过利用targeting proportion γ和删除概率α，将随机性引入到了这个过程中。

其中targeting proportion表示会选择最小的γ|θ|个权重作为Dropout的候选权值，并且随后以删除概率α独立地去除候选集合中的权值。这意味着在Targeted Dropout中每次权重更新所保留的单元数为(1−γ*α)|θ|。

正如在后文所看到的，Targeted Dropout降低了重要子网络对不重要子网络的依赖性，因此降低了对已训练神经网络进行剪枝的性能损失。如下表1和表2所示，权重剪枝实验表示正则化方案的基线结果要比Targeted Dropout差，并且应用了Tageted Dropout的模型比不加正则化的模型性能更好，且同时参数量只有一半。通过在训练过程中逐渐将targeting proportion由0增加到99%，最终表示该方法能获得极高的剪枝率。

https://github.com/for-ai/TD/tree/master/models