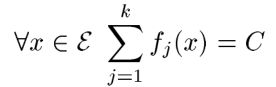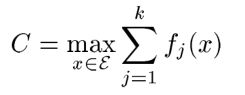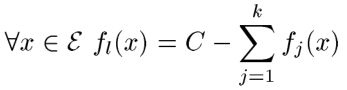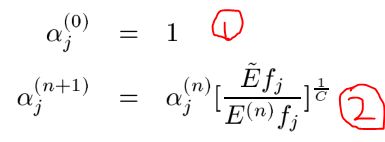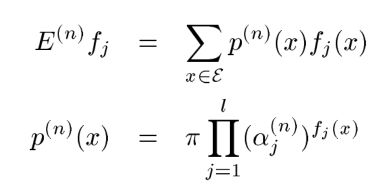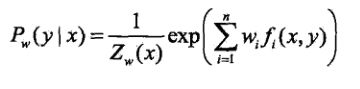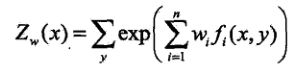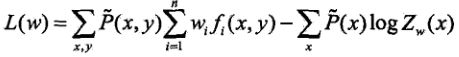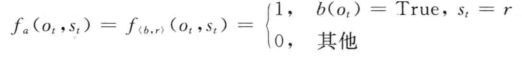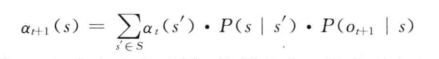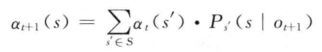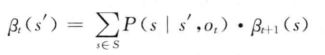NLP --- 最大熵模型的解法（GIS算法、IIS算法）

上一节中我们详细的介绍了什么是最大熵模型，也推导出了最大熵模型的目标公式，但是没给出如何求解的问题，本节将详细讲解GIS算法求解最大熵模型的过程，这里先把上一节的推导出的公式拿过来：

上面第一个式子是说我们要寻找的P要满足k个约束条件，下式说是在满足的约束的情况下，找到是熵值最大的那个P。下面给出的形式：

上式是指数族表达式，只有一个未知数即，其中是归一化因子，一旦约束条件确定，那么归一化因子就确定了，为什么要有归一化因子呢？因为总概率和为1这个条件必须得满足的。所以现在我们需要求出（2）的未知数即，怎么求呢？需要通过GIS算法，下面就详细的介绍GIS算法。

GIS算法（Generalized Iterative Scaling）

本节还是参考那篇文章即《A Simple Introduction to Maximum Entropy Models for Natural Language Processing》，大家可以对照看一下，下面正式开始本节的内容：

首先我们先使所有特征函数的和等于C，如下：

那可能就有人怀疑了，这个C怎么确定才能满足呢？这里给出一种可能：

既然取得是最大的，那么就有可能不满足上式，怎么办呢？这里引入一个矫正函数，和上面的形式一样，怎么确定这个矫正函数呢？如下所示：

上式挺暴力的，如果不满足，我把剩下的直接付给一个函数，然后在加上去就满足了，确实满足了。其实这样做对后面的计算没什么影响，我们继续往下看;

这里我们需要先假设至少存在一个特征函数为1，目的是总概率必须为1，如下：

下面我们就看看如何求解：

                                                                

其中：

 

如①式第一次迭代说明刚开所有的特征的概率相等，此时的熵是最大的，这个可以为1 ，那么上面的第②式子就是迭代了，其实第二个式子很简单，大家不要把他们理解的太难了，我们一起来看看他是如何迭代的， 其中是原始的特征期望或者说是约束条件的和，而是第n次迭代得到的期望，那么他们的比值说明了什么呢，如果第n次迭代的结果偏大即 偏大，则比值会小于1，那么乘上小于1的数就会使得第n+1的值减小即比小，这样就会不断的向着最优解靠近了，和EM的思想差不多，这里大家需要好好理解。

GIS的大概思路就是这样的，但是这个算法虽然可以求解我们的最大熵模型，但是计算量太大了，以至于使用受限，计算量主要体现在哪里呢？计算量主要在自然语言处理的特征很多的，有时一个文本中的特征有上百万个，而每个特征都要参与上面的计算，而且还要不停的多次迭代，这就导致了计算量很大的原因，因此这个算法的使用受到了限制，那如何改进呢？后来
Vincent J. Della Pietra  提出了改进型的迭代算法即IIS算法（Improved Iterative Scaling），他是如何改进计算量的呢？我们下面看看：

 IIS算法（Improved Iterative Scaling）

其实IIS和GIS很类似，不同之处在于GIS算法有一个矫正项，目的是使的所有特征特征等于一个常数C，但是并没有那么容易满足，因此IIS的和他不同之处就是我可以不用非要满足这个所有特征等于一个常数，如果等于C就按照GIS进行求解，如果不满足就按照牛顿法进行求解即可。下面直接给出原始论文的IIS算法过程，当然看李航的书也是一样的，只是写的方式有点不一样，论文里是使用表示指数族，而李航的未知数直接放在以e为底的指数上了，大家需要注意区别，同时IIS算法出自这篇论文

《A Maximum Entropy Approach to Natural Language Processing》Vincent J. Della Pietra ，下面给出这篇论文的算法过程：

 

这里建议先看看李航先生的书即《统计学习方法》的第六章的最大熵模型，如果大家对上一节的原理搞明白了，那么看他的书还是很容易理解的，只是使用的表达式不一样吧了，虽然都是指数族函数，但是他那本书使用的是以自然对数的指数族函数，原理和我们上一节是一样的，只是求解最大熵模型的思路不一样，我们上面使用的是GIS算法进行求解，李航先生的书是根据拉格朗日乘子进行求解的，其实他的主要思路是我们上一节不是有两个约束条件吗，如果大家理解支持向量机的话，理解他的解决思路就很简单了，这里不懂的建议还是系统的把支持向量机学习一下吧，我在机器学习模块中对此进行了详细的讲解，这里大家可以去看看。他把含有约束条件的求解最大熵模型通过拉格朗日乘子法，把约束条件和目标式子合二为一，通过对偶问题进行求解，最后就得到一个最大的概率含参数的模型，通过样本就可以求出参数，最后就可以确定了参数的值，这就是李航的解法。后面李航的书继续介绍了最优化算法，即IIS算法，讲解的很详细，这里就不细讲了，也不做搬运工了，大家可以找到这本书好好研究，当然需要你有很好的数学基础，如果你对SVM的理解很深入，我觉的看他的书是一种享受，他写的很简明扼要，里面会有大量的数学公式，看起来也很顺利，这里简单的把IIS算法的过程讲解一下，细节部分，建议看李航的书。

已知最大熵模型为：

其中：

  上式L(w)就是通过拉格朗日乘子法最后确定的模型，通过极大释然估计求得w就求出了最大熵模型的参数了。

详细的推倒过程请查看李航的书，这里不再赘述了。请大家一定要好好看看那一章，一定要深入理解他们，这里我就偷懒了，不再叙述了。下面简单的介绍一下把最大熵模型和隐马尔可夫结合在一起的应用。

MEMM（maximum-entropy Markov model,MEMM）

最大熵马尔可夫模型(maximum-entropy Markov model，MEMM）又称条件马尔可夫模型（conditionalMarkovmodel，CMM)，由Andrew McCallum，DayneFreitag和FernandoPereira二人于2000年提出[McCallum，2000〕。它结合了隐马尔可夫模型和最大熵模型的共同特点，被广泛应用于处理序列标注问题。文献[McCallumal.，2000]认为，在HMM模型中存在两个问题：．在很多序列标注任务中，尤其当不能枚举观察输出时，需要用大量的特征来刻画观察序列。如在文本中识别一个未见的公司名字时，除了传统的单词识别方法以外，还需要用到很多特征信息，如大写字母、结尾词、词性、格式、在文本中的位置等。也就是说，我们需要用特征对观察输出进行参数化。(2)在很多自然语言处理任务中，需要解决的问题是在已知观察序列的情况下求解状态序列，HMM采用生成式的联合概率模型（状态序列与观察序列的联合概率来求解这种条件概率问题，这种方法不适合处理用很多特征描述观察序列的情况。为此，MEMM直接采用条件概率模型，从而使观察输出可以用特征表示，借助最大熵框架进行特征选取。

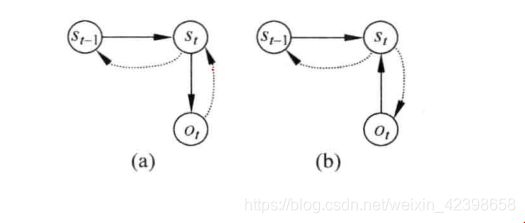
MEMM主要求解HMM的第二个问题，因此这里我们看看他们二者的区别：

 （a）为传统HMM的依存关系图，实线箭头表示所指的结点依赖于箭头起始结点，虚线箭头表示箭头所指的结点是起始结点条件。图（b）为MEMM的依存关系图。在HMM中解码过程求解的是，而在MEMMM中解码器

 求解的是。在HMM中，当前时刻的观察输出只取决于当前状态，而在MEMM中，当前时刻的观察输出还可能取决于前一时刻的状态。假设已知观察序列研，要求解状态序列，并使条件概率最大。在MEMM中，将这一概率因子化为马尔可夫转移概率，该转移概率依赖于当前时刻的观察和前一时刻的状态：

对于前一时刻每个可能的状态取值的概率通过最大熵分类器建模和当前观察输出，当前状态取值

其中，为归一化因子，为特征函数，为特征函数的权重，可以利用GIS算法，从训练样本中估计出来。可以通过定义，其中，b是当前观察的{0，1}二值特征，是状态取值。

HMM中用于参数估计的Baum-Welch算法修改后可用于MEMM的状态转移概率估计。在Viterbi算法中，如果t时刻到达状态5时产生观察序列的前向概率为,那么，

在MEMM中，将定义为在时刻t的状态为s,给定到达t时刻为止的观察序列时的前向概率：

相应的后向概率为在给定t时刻之后的观察序列时，从t时刻、状态开始的概率：

MEMM是有向图和无向图的混合模型，其主体还是有向图框架。与HMM相比，MEMM的最大优点在于它允许使用任意特征刻画观察序列，这一特性有利于针对特定任务充分利用领域知识设计特征。MEMM与HMM和条件随机场(conditional random fields，CRFs)模型相比，MEMM的参数训练过程非常高效，在HMM和CRF模型的训练中，需要利用前向后向算法作为内部循环，而在MEMM中估计状态转移概率时可以逐个独立进行。MEMM的缺点在于存在标记偏置问题（labelbiasproblem)，其中一个原因是熵低的状态转移分布会忽略它们的观察输出，而另一个原因是MEMM像HMM一样，其参数训练过程是自左向右依据前面已经标注的标记进行的，一旦在实际测试时前面的标记不能确定时，MEMM往往难以处理。

下一节我们在这个基础上进行引入条件随机场。