PyTorch神经网络中可学习的参数——CNN权重 | PyTorch系列(十五)
点击上方“AI算法与图像处理”,选择加"星标"或“置顶”
重磅干货,第一时间送达![]()
文 |AI_study
我们的神经网络
在本系列的最后几篇文章中,我们已经开始构建CNN,我们做了一些工作来理解我们在网络构造函数中定义的层。
class Network(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
self.conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)
self.fc1 = nn.Linear(in_features=12*4*4, out_features=120)
self.fc2 = nn.Linear(in_features=120, out_features=60)
self.out = nn.Linear(in_features=60, out_features=10)
def forward(self, t):
# implement the forward pass
return t
最后,我们在整个过程中的下一步是在网络的 forward 方法中使用这些层,但是现在,让我们来看看网络中的可学习参数。
我们已经知道了超参数。我们知道超参数的值是任意选取的。
到目前为止,我们使用的超参数是我们用来构建网络架构的参数,尽管我们构建的层被赋值为类属性。
Hyperparameter values are chosen arbitrarily.
这些超参数并不是唯一的超参数,当我们开始训练过程时,我们将看到更多的超参数。我们现在关心的是网络的可学习参数。
可学习的参数
可学习参数 是指在训练过程中学习的参数值。
对于可学习的参数,我们通常从一组随机值开始,然后随着网络的学习,以迭代的方式更新这些值。
事实上,当我们说网络是学习的时候,我们的具体意思是网络正在学习可学习参数的适当值。这些值是使损失函数最小化的值。
当涉及到我们的网络时,我们可能会想,这些可学习的参数在哪里?
Where are the learnable parameters?
我们将可学习的参数是网络内部的权重,它们存在于每一层中。
获取网络的实例
在PyTorch中,我们可以直接检查权重。让我们获取我们的网络类的一个实例并查看它。
network = Network()
请记住,要获取我们的网络类的对象实例,我们需要在类名后面加上括号。当这段代码执行时,__init__ 类构造函数中的代码将运行,分配给层返回的对象实例之前的属性。
名称为__init__ 是initialize的缩写。在对象的情况下,属性是使用值来初始化的,这些值实际上可以是其他对象。通过这种方式,对象可以嵌套在其他对象中。
我们的网络类就是这种情况,其网络类属性是使用PyTorch 层类的实例初始化的。初始化对象后,我们可以使用网络变量访问对象。
在开始使用新创建的网络对象之前,请查看将网络传递给Python的print() 函数时会发生什么。
print(network)
Network(
(conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
(conv2): Conv2d(6, 12, kernel_size=(5, 5), stride=(1, 1))
(fc1): Linear(in_features=192, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=60, bias=True)
(out): Linear(in_features=60, out_features=10, bias=True)
)
print() 函数将控制台的字符串表示形式输出到控制台。凭着敏锐的眼光,我们可以注意到这里的打印输出详细说明了我们网络的结构,列出了我们网络的层,并显示了传递给层构造函数的值。
网络的字符串表示
不过,有一个问题。这是怎么回事?
Where is this string representation coming from?
我们的网络类将从PyTorch Module基类继承此功能。观察如果我们停止扩展神经网络模块类会发生什么。
print(network)
<__main__.Network object at 0x0000017802302FD0>
现在,我们没有像以前那样好的描述性输出。取而代之的是,我们得到了一堆奇怪的内容,如果我们不提供这是默认的Python字符串表示形式。
因此,在面向对象的编程中,我们通常希望在类中提供对象的字符串表示形式,以便在打印对象时获得有用的信息。这种字符串表示形式来自Python的默认基类object(对象)。
How Overriding Works
所有Python类都会自动扩展对象类。如果我们想为我们的对象提供一个自定义的字符串表示形式,我们可以做到,但是我们需要引入另一个面向对象的概念,称为overriding(覆盖)。
当我们扩展一个类时,我们获得了它的所有功能,作为补充,我们可以添加其他功能。但是,我们也可以通过将现有功能更改为不同的行为来覆盖现有功能。
我们可以使用__repr__函数覆盖Python的默认字符串表示。这个名称是representation(表示)的缩写。
def __repr__(self):
return "lizardnet"
这一次,当我们将网络传递给print函数时,我们在类定义中指定的字符串将代替Python的默认字符串打印出来。
> print(network)
lizardnet
当我们在前面讨论OOP时,我们了解了__nit__方法,以及它是如何作为一种特殊的Python方法来构造对象的。
我们还会遇到其他特殊的方法,而__repr__就是其中之一。所有特殊的OOP Python方法通常都有双下划线的前缀和后缀。
这也是PyTorch模块基类的工作方式。模块基类覆盖了_repr__函数。
字符串表示的是什么
在大多数情况下,PyTorch提供的字符串表示与我们根据配置网络层的方式所期望的基本一致。
但是,还有一些额外的信息需要强调。
卷积层
对于卷积层,kernel_size参数是一个Python元组(5,5),尽管我们只在构造函数中传递了数字5。
Network(
(conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
(conv2): Conv2d(6, 12, kernel_size=(5, 5), stride=(1, 1))
(fc1): Linear(in_features=192, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=60, bias=True)
(out): Linear(in_features=60, out_features=10, bias=True)
)
这是因为我们的滤波器实际上有一个高度和宽度,当我们传递一个数字时,该层构造函数中的代码假设我们需要一个方形滤波器(filter)。
self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
self.conv2 = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=5)
stride是一个我们可以设置的额外参数,但是我们把它省略了。当在层构造函数中没有指定stride时,层会自动设置它。
stride 告诉conv层,在整个卷积中,每个操作之后滤波器应该滑动多远。这个元组表示当向右移动时滑动一个单元,向下移动时也滑动一个单元。
Linear 层
对于Linear 层,我们有一个额外的参数bias,它的默认参数值为true。可以通过将它设置为false来关闭它。
self.fc1 = nn.Linear(in_features=12*4*4, out_features=120)
self.fc2 = nn.Linear(in_features=120, out_features=60)
self.out = nn.Linear(in_features=60, out_features=10)
关于打印对象时显示的信息,有一点需要注意,那就是它是完全任意的信息。
作为开发人员,我们可以决定将任何信息放在那里。然而,Python文档告诉我们,信息应该足够完整,以便在需要时可以用来重构对象。
https://docs.python.org/3/reference/datamodel.html#object.__repr__
访问网络层
好了,现在我们已经有了一个网络实例,我们已经检查了我们的层,让我们看看如何在代码中访问它们。
在Python和许多其他编程语言中,我们使用点符号访问对象的属性和方法。
> network.conv1
Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
> network.conv2
Conv2d(6, 12, kernel_size=(5, 5), stride=(1, 1))
> network.fc1
Linear(in_features=192, out_features=120, bias=True)
> network.fc2
Linear(in_features=120, out_features=60, bias=True)
> network.out
Linear(in_features=60, out_features=10, bias=True)
这就是点表示法。用点表示法,我们用点来表示我们想要打开对象并访问里面的东西。我们已经用过很多次了,这里提到的只是给这个概念一个标签。
关于这一点需要注意的是与我们刚刚讨论的网络的字符串表示直接相关的是,这些代码片段中的每一段也为我们提供了每一层的字符串表示。
在网络的情况下,网络类实际上只是将所有这些数据编译在一起,从而给出一个单独的输出。
Network(
(conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
(conv2): Conv2d(6, 12, kernel_size=(5, 5), stride=(1, 1))
(fc1): Linear(in_features=192, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=60, bias=True)
(out): Linear(in_features=60, out_features=10, bias=True)
)
关于这些对象的字符串表示的最后一件事是,在本例中,我们实际上并没有使用print方法。
我们仍然获取字符串表示的原因是我们使用的是Jupyter notebook,而在后台notebook正在访问字符串表示,因此它可以向我们显示一些内容。这是字符串表示的主要用例的一个很好的例子。
访问层权重
现在我们已经访问了每一层,我们可以访问每一层中的权重。我们来看看第一个卷积层。
> network.conv1.weight
Parameter containing:
tensor([[[[ 0.0692, 0.1029, -0.1793, 0.0495, 0.0619],
[ 0.1860, 0.0503, -0.1270, -0.1240, -0.0872],
[-0.1924, -0.0684, -0.0028, 0.1031, -0.1053],
[-0.0607, 0.1332, 0.0191, 0.1069, -0.0977],
[ 0.0095, -0.1570, 0.1730, 0.0674, -0.1589]]],
[[[-0.1392, 0.1141, -0.0658, 0.1015, 0.0060],
[-0.0519, 0.0341, 0.1161, 0.1492, -0.0370],
[ 0.1077, 0.1146, 0.0707, 0.0927, 0.0192],
[-0.0656, 0.0929, -0.1735, 0.1019, -0.0546],
[ 0.0647, -0.0521, -0.0687, 0.1053, -0.0613]]],
[[[-0.1066, -0.0885, 0.1483, -0.0563, 0.0517],
[ 0.0266, 0.0752, -0.1901, -0.0931, -0.0657],
[ 0.0502, -0.0652, 0.0523, -0.0789, -0.0471],
[-0.0800, 0.1297, -0.0205, 0.0450, -0.1029],
[-0.1542, 0.1634, -0.0448, 0.0998, -0.1385]]],
[[[-0.0943, 0.0256, 0.1632, -0.0361, -0.0557],
[ 0.1083, -0.1647, 0.0846, -0.0163, 0.0068],
[-0.1241, 0.1761, 0.1914, 0.1492, 0.1270],
[ 0.1583, 0.0905, 0.1406, 0.1439, 0.1804],
[-0.1651, 0.1374, 0.0018, 0.0846, -0.1203]]],
[[[ 0.1786, -0.0800, -0.0995, 0.1690, -0.0529],
[ 0.0685, 0.1399, 0.0270, 0.1684, 0.1544],
[ 0.1581, -0.0099, -0.0796, 0.0823, -0.1598],
[ 0.1534, -0.1373, -0.0740, -0.0897, 0.1325],
[ 0.1487, -0.0583, -0.0900, 0.1606, 0.0140]]],
[[[ 0.0919, 0.0575, 0.0830, -0.1042, -0.1347],
[-0.1615, 0.0451, 0.1563, -0.0577, -0.1096],
[-0.0667, -0.1979, 0.0458, 0.1971, -0.1380],
[-0.1279, 0.1753, -0.1063, 0.1230, -0.0475],
[-0.0608, -0.0046, -0.0043, -0.1543, 0.1919]]]],
requires_grad=True
)
输出是一个张量,但在我们研究这个张量之前,我们先来讨论一下OOP。这是一个很好的例子,展示了对象是如何嵌套的。我们首先访问位于网络对象内部的conv层对象。
network.conv1.weight
然后,我们访问权张量对象,它位于conv层对象内部,所以所有这些对象都链接在一起。
关于权张量的输出有一件事需要注意,它说的是输出顶部包含的参数。这是因为这个特殊的张量是一个特殊的张量因为它的值或者标量分量是我们网络的可学习参数。
这意味着这个张量里面的值,就是我们上面看到的那些,实际上是在网络训练的过程中习得的。当我们训练时,这些权值会以使损失函数最小化的方式更新。
PyTorch参数类
跟踪网络中所有的张量权重。PyTorch有一个特殊的类,称为Parameter。Parameter类扩展了张量类,所以每层中的权张量就是这个Parameter类的一个实例。这就是为什么我们会在字符串表示输出的顶部看到包含文本的参数。
我们可以在Pytorch源代码中看到,Parameter类通过将包含正则张量类表示输出的文本参数放在前面,从而覆盖了__repr__函数。
def __repr__(self):
return 'Parameter containing:\n' + super(Parameter, self).__repr__()
PyTorch的nn.Module类基本上是在寻找其值是Parameter类的实例的任何属性,当它找到参数类的实例时,就会对其进行跟踪。
所有这些实际上都是在幕后进行的PyTorch技术细节,我们将看到其中的一部分。
现在就我们的理解而言,重要的部分是张量权重形状的解释。在这里,我们将开始使用在本系列早期学习的关于张量的知识。
现在让我们看一下这些形状,然后对其进行解释。
张量权重形状
在上一篇文章中,我们说过传递给层的参数值会直接影响网络的权重。在这里将看到这种影响。
对于卷积层,权重值位于滤波器内部,而在代码中,滤波器实际上是权重张量本身。
层内的卷积运算是该层的输入通道与该层内的滤波器之间的运算。这意味着我们真正拥有的是两个张量之间的运算。
话虽如此,让我们解释这些权重张量,这将使我们更好地了解网络内部的卷积操作。
请记住,张量的形状实际上编码了我们需要了解的有关张量的所有信息。
对于第一个conv 层,我们有1个颜色通道,应由6个5x5大小的滤波器进行卷积以产生6个输出通道。这就是我们解释层构造函数中的值的方式。
> network.conv1
Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
不过,在层内部,对于这6个滤波器,我们没有明确地有6个权重张量。实际上,我们使用单个权重张量表示所有6个滤波器,其形状反映或说明了6个滤波器。
第一卷积层的权重张量的形状告诉我们,我们有一个4阶权重张量。第一个轴的长度为6,这说明了6个滤波器。
> network.conv1.weight.shape
torch.Size([6, 1, 5, 5])
第二个轴的长度为1,代表单个输入通道,最后两个轴的长度和宽度代表滤波器。
考虑这一点的方式就像我们将所有滤波器打包到一个张量中一样。
现在,第二个conv层具有12个滤波器,不是单个输入通道,而是有6个来自上一层的输入通道。
> network.conv2.weight.shape
torch.Size([12, 6, 5, 5])
在这里将此值 6 赋予每个滤波器一定的深度。我们的滤波器具有的深度与通道数匹配,而不是让滤波器迭代地对所有通道进行卷积。
关于这些卷积层的两个主要方面是,我们的滤波器使用单个张量表示,并且张量内的每个滤波器也具有一个深度,该深度说明了正在卷积的输入通道。
所有滤波器均使用单个张量表示。
滤波器的深度由输入通道决定。
我们的张量是4阶张量。第一个轴代表滤波器的数量。第二个轴代表每个滤波器的深度,它对应于卷积的输入通道数。
最后两个轴代表每个过滤器的高度和宽度。我们可以通过索引权重张量的第一轴来拉出任何单个滤波器。
(Number of filters, Depth, Height, Width)
这给我们提供了一个高度和宽度为5,深度为6的滤波器。
权重矩阵
对于线性层或完全连接的层,我们将张量展平一阶作为输入和输出。我们将线性层中的in_features转换为out_features的方式是使用通常称为权重矩阵的2阶张量。
这是由于权重张量在高度和宽度轴上均为2阶。
> network.fc1.shape
torch.Size([120, 192])
> network.fc2.shape
torch.Size([60, 120])
> network.out.shape
torch.Size([10, 60])
在这里,我们可以看到每个线性层都有一个2阶的权重张量。我们在这里可以看到的模式是权重张量的高度具有所需输出特征的长度和输入特征的宽度。
一、矩阵乘法
这个事实是由于矩阵乘法是如何执行的。让我们通过一个较小的示例来了解这一点。
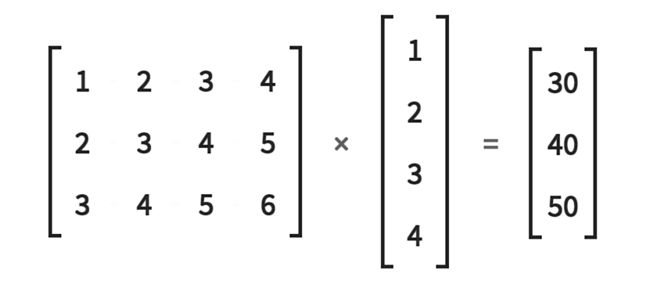
假设我们有两个2阶张量。第一个形状为3x4,第二个形状为4x1。现在,由于我们要演示的是矩阵乘法,因此请注意,这两个2阶张量的确是矩阵。
对于输出中的每个行-列组合,通过获取第一矩阵的相应行与第二矩阵的相应列的点积来获得该值。
由于本示例中的第二个矩阵仅具有1列,因此我们将其全部使用了3次,但是这种想法是通用的。
该操作起作用的规则是,第一个矩阵中的列数必须与第二个矩阵中的行数匹配。如果该规则成立,则可以执行这样的矩阵乘法运算。
点积意味着我们将相应组件的乘积相加。如果您想知道,点积和矩阵乘法都是线性代数概念。
二、使用矩阵表示的线性函数
像这样的矩阵乘法的重要之处在于它们代表了可以用来构建神经网络的线性函数。
具体而言,权重矩阵是线性函数,也称为线性映射,该线性映射将4维的向量空间映射到3维的向量空间。
当我们更改矩阵内的权重值时,实际上是在更改此函数,而这恰恰是我们在搜索网络最终逼近的函数时要执行的操作。
让我们看看如何使用PyTorch执行相同的计算。
三、使用PyTorch进行矩阵乘法
在这里,我们使用in_features和weight_matrix作为张量,并使用名为matmul() 张量方法执行操作。我们现在知道的名称matmul() 矩阵乘法的缩写。
> weight_matrix.matmul(in_features)
tensor([30., 40., 50.])
一个迫在眉睫的问题是,我们如何才能一次访问所有参数?有一个简单的方法。让我告诉你。
访问网络参数
第一个示例是最常见的方法,我们将在训练过程中更新权重时使用它来遍历权重。
for param in network.parameters():
print(param.shape)
torch.Size([6, 1, 5, 5])
torch.Size([6])
torch.Size([12, 6, 5, 5])
torch.Size([12])
torch.Size([120, 192])
torch.Size([120])
torch.Size([60, 120])
torch.Size([60])
torch.Size([10, 60])
torch.Size([10])
第二种方法只是显示如何也可以看到该名称。这揭示了我们将不详细介绍的内容,偏差也是可学习的参数。默认情况下,每个层都有一个偏差,因此对于每个层,我们都有一个权重张量和一个偏差张量。
for name, param in network.named_parameters():
print(name, '\t\t', param.shape)
conv1.weight torch.Size([6, 1, 5, 5])
conv1.bias torch.Size([6])
conv2.weight torch.Size([12, 6, 5, 5])
conv2.bias torch.Size([12])
fc1.weight torch.Size([120, 192])
fc1.bias torch.Size([120])
fc2.weight torch.Size([60, 120])
fc2.bias torch.Size([60])
out.weight torch.Size([10, 60])
out.bias torch.Size([10])
现在,我们应该对可学习的参数,网络内部的位置以及如何使用PyTorch访问权重张量有了很好的了解。
在下一篇文章中,我们将了解如何通过将张量传递给层来处理它们。
文章中内容都是经过仔细研究的,本人水平有限,翻译无法做到完美,但是真的是费了很大功夫,希望小伙伴能动动你性感的小手,分享朋友圈或点个“在看”,支持一下我 ^_^
英文原文链接是:
https://deeplizard.com/learn/video/stWU37L91Yc
![]()
![]()
![]()
加群交流
![]() 欢迎小伙伴加群交流,目前已有交流群的方向包括:AI学习交流群,目标检测,秋招互助,资料下载等等;加群可扫描并回复感兴趣方向即可(注明:地区+学校/企业+研究方向+昵称)
欢迎小伙伴加群交流,目前已有交流群的方向包括:AI学习交流群,目标检测,秋招互助,资料下载等等;加群可扫描并回复感兴趣方向即可(注明:地区+学校/企业+研究方向+昵称)
![]()
![]()
谢谢你看到这里! ????