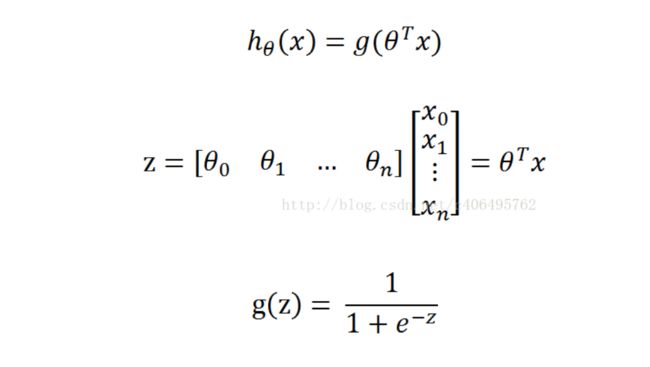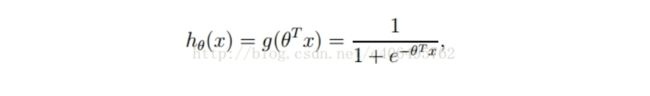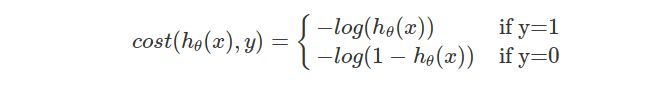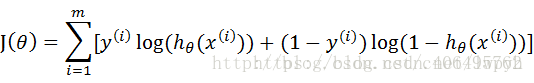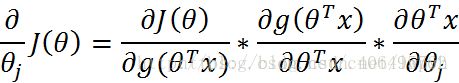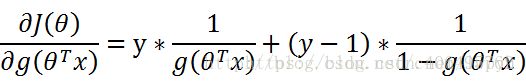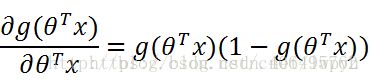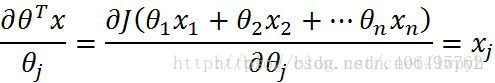《机器学习实战》 (3) logistic regression(逻辑斯蒂回归)小结(上)
更新:代码在这里:https://github.com/lwpyh/machinelearning-in-action
最近一直在学习《机器学习实战》这一本书,之前学习了kNN 算法和决策树算法,因为想迫切的接触logistic回归算法,所以我跳过了朴素贝叶斯(下一讲会说),而是首先学习了logistic回归,这也是在实际工作中最为普遍的一种模型,但是这个模型有趣就有趣在虽然模型最为古老,思路也最为清晰,但是不仅内涵丰富而且对于实际工作中的许多问题也是最为有效的,下面就结合《机器学习实战》logistic回归的相关案例来手把手学习logistic回归问题。因为要了解logistics回归,就必须了解其数学本质,所以为了保证大家能明白代码的含义,也不使篇幅过长,本讲讲分为上下两讲,第一讲是logistics回归的数学推导和基本模型建立,第二讲结合《机器学习实战》对logistics回归做实战分析。
一。logistics回归曲线的数学原理
logistics回归的 思路非常简单,本质而言就是一个二类分类器,本质上与线性感知机一样,是对两个类进行分类,区别在于线性回归(即感知机)的分类边界曲线是一条直线,一旦出现两类交织的情况就GG了,但是logistics回归由于有激活函数sigmoid函数的存在,导致了将分类曲线由一条直线变成了可以弯曲的曲线,有效的适应了很大一部分实际情况,所以应用更为广泛。由于该模型是根据已有的数据来判别数据点的类型,所以该模型是一种生成模型。logistics函数的公式如下所示:
通俗的解释就是 对于下面的这个数据集构成的二类点集合,(红点和蓝点两类)
回归模型的功能就是能够找到一条边界决策曲线,使边界决策曲线两侧均为不同的类。其中前文中的x表示的就是不同的自变量(如各个影响因素,θ就是对应的不同自变量x的权重,因为θ与X数目肯会很多,所以采用矩阵形式进行计算,可以加快运算速度,运算得出的结果范围会很大,可以取到所有实数,但是实际上的取值目标是只要分出2类即可,即若为第一类,设为0否则结果为1,为了将结果转化到[0,1]范围之内,就需要通过一个激活函数,这里选用sigmoid函数来实现,即g(z)
从图中可以看到输入域为实数域,输出域为[0,1],这样将输出域缩小到[0,1]范围内,同时该函数具有一个特性,只要输出大于0,输出就会快速接近1,反之会快速接近0,这样就会使结果几乎不是1就是0,从而实现了快速分类,为了更加合理,我们假设若输出大于0.5,为1类,否则为0类。但是输出的结果对不对需要将结果与真实值进行对比,通过差值反馈来实现模型输出的矫正,即对θ进行调整,实现与真实值接近。
在线性回归中,通过损失函数的最小化来实现输出值的逼近,损失函数在 线性函数中的定义是输出与实际标签差值的平方和的平均值,该值越小,模型越准确。对本问题就可以进行微调,即在x,θ为某一参数条件下的分类为1或0的条件概率,依次为:
这里的概率值直接用sigmoid函数输出值表示,当输出大于0.5的时候,概率直接用输出值表示,而类别用1来表示,当输出小于0.5时,概率用1-输出值表示,类别用0来表示。这样统一以后,概率越大,为该类的可能性越大,符合我们的认识。在离散条件下得到的代价函数(cost function)用对数似然损失函数,其表达形式是:
稍微解释下这个损失函数,或者说解释下对数似然损失函数:
当y=1时,假定这个样本为正类。如果此时hθ(x)=1,则单对这个样本而言的cost=0,表示这个样本的预测完全准确。那如果所有样本都预测准确,总的cost=0
但是如果此时预测的概率hθ(x)=0,那么cost→∞。直观解释的话,由于此时样本为一个正样本,但是预测结果 P(y=1|x;θ)=0
, 也就是说预测 y=1的概率为0,那么此时就要对损失函数加一个很大的惩罚项。 当y=0时,推理过程跟上述完全一致,不再累赘。
将以上两个表达式合并为一个,则单个样本的损失函数可以描述为:
这样就可以将两个不同类的代价函数统一起来了,这个代价函数,是对于一个样本而言的。给定一个样本,我们就可以通过这个代价函数求出,样本所属类别的概率,而这个概率越大越好,所以也就是求解这个代价函数的最大值。既然概率出来了,那么最大似然估计也该出场了。假定样本与样本之间相互独立,那么整个样本集生成的概率即为所有样本生成概率的乘积,再将公式对数化,便可得到如下公式: 
其中,m为样本的总数,y(i)表示第i个样本的类别,x(i)表示第i个样本的对应数据集,需要注意的是θ是多维向量,x(i)也是多维向量。所以只要找到使J(θ)最大的值即为目标模型最准确的地方,故使用梯度上升法,在一些教程中,上式结果前有一个负号,此时需要求出最小值,用梯度下降法,这是二者差异产生的地方。
这里我们使用梯度上升法,找到是J(θ)最大的地方,即使所有样本结果为使现有数据条件下结果可能性最大的那种情况(极大似然函数的定义)梯度上升法的定义是 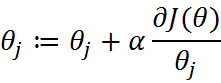
sigmoid函数为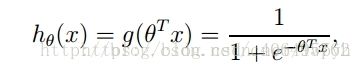 ,所以目标就是对J(θ)的θ求偏导,找到θ使J(θ)最大。
,所以目标就是对J(θ)的θ求偏导,找到θ使J(θ)最大。
二.Python实现logistics回归最基本模型
前文已经叙述了logistics回归的基本数学原理,现在结合《机器学习实战》的具体代码进行解释。
首先是编写数据集函数:
import numpy as np#导入numpy库
import random
def loadDataSet():#加载数据集函数
dataMat=[]#数据集预留矩阵
labelMat=[]#标签集预留矩阵
fr=open('machinelearning/Ch05/testSet.txt')#打开数据集并存在fr里
for line in fr.readlines():#按行读入
lineArr=line.strip().split()#去回车载入数据
dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])])#把每行的第一第二个数据作为数据集
labelMat.append(int(lineArr[2]))#每行第三个作为标签
return dataMat,labelMat然后是激活函数和梯度上升函数
def sigmoid(inX):#激活函数
return (1.0/(1.0+np.exp(-inX)))
def gradDesent(dataMatIn,classLabels):#梯度下降
dataMatrix=np.mat(dataMatIn)#导入数据转成numpy格式矩阵
labelMat=np.mat(classLabels).transpose()#将标签矩阵转置
m,n=np.shape(dataMatrix)#将导入数据矩阵的长和宽附给m和n
alpha=0.001#每次的步率为0.01
maxCycles=50000#重复次数
weights=np.ones((n,1))#权重初值矩阵
for k in range(maxCycles):#循环执行梯度下降法
h=sigmoid(dataMatrix*weights)#处理后为100*1矩阵
error=(labelMat-h)
weights=weights+alpha*dataMatrix.transpose()*error#这里不是直接求偏导,而是求导后的式子直接带入,此时3*1矩阵
return weights.getA()为了显示出具体分布情况,再编写一个可视化函数
def plotBestFit(weights):#画图函数
import matplotlib.pyplot as plt #载入matplotlib
dataMat,labelMat=loadDataSet()#载入数据集和标签集
dataArr=np.array(dataMat)#把数据转化为numpy矩阵
n=np.shape(dataMat)[0]#获取第一列行数,即数据个数
xcord1=[]#正样本
ycord1=[]#正样本
xcord2=[]#负样本
ycord2=[]#负样本
for i in range(n):
if int(labelMat[i]==1):#正样本归类
xcord1.append(dataArr[i,1])
ycord1.append(dataArr[i,2])
else:#负样本归类
xcord2.append(dataArr[i,1])
ycord2.append(dataArr[i,2])
fig=plt.figure()
ax=fig.add_subplot(111)#添加subplot
ax.scatter(xcord1,ycord1,s=20,c='red',marker='s',alpha=.5)#绘制正样本
ax.scatter(xcord2,ycord2,s=20,c='green',alpha=.5)#绘制负样本
x=np.arange(-3.0,3.0,0.1)
y=(-weights[0]-weights[1]*x)/weights[2]#分界线,即sigmoid为0时的曲线应该为分界线,此时的x1与x2关系曲线
ax.plot(x,y)#x,y绘在图纸上
plt.title('BestFit')
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()利用jupyter notebook编译上述函数
首先获得500次迭代后该数据集的权重矩阵
再调用可视化处理函数,观察实际效果
这就是logistics回答分类的基本原理与基本方法的实践,其实在实践中,每次变化的步率和求偏导的方法还是有许多变种的,下一讲会详细说明。
参考文献:
- 斯坦福大学的吴恩达《机器学习》:https://www.coursera.org/learn/machine-learning
- 《机器学习实战》第五章内容
- CSDN博客:点击打开链接