Seq2Seq and Attention 入门
Seq2Seq and Attention
参考文献
[1] Cho 在 2014 年在论文《Learning Phrase Representations using RNN Encoder–Decoder
for Statistical Machine Translation》中提出 Encoder–Decoder 结构
[2] Sutskever et al 2014年在论文 《Sequence to Sequence Learning with Neural Networks》中正式提出seq2seq的概念
[3] Dzmitry Bahdanau, Kyunghyun Cho, Yoshua Bengio.在论文
《Neural Machine Translation by Jointly Learning to Align and Translate》 ICLR 2015.中提出BahdanauAttention Mechanism。
[4] Minh-Thang Luong, Hieu Pham, Christopher D. Manning.在论文
《”Effective Approaches to Attention-based Neural Machine Translation.”
EMNLP 2015.》中提出LuongAttention Mechanism.
1. Seq2Seq model
seq2seq的名字全称是序列到序列(sequence to sequence), 从一个序列到另一个序列,可以是从中文的序列到英文的序列,也可以是从中文语音序列到中文文字序列,总之,实现的是从一个不定长输入序列到一个不定长输出序列的模型。
1.1 Encoder-Decoder model
要实现从一个序列到另外一个序列的转换,正常思维逻辑是找到一个中间编码,可以实现在两种序列之间实现自由转换。于是乎,Encoder-Decoder结构在2014年被Cho提了出来, 先通过编码器对原序列进行编码,再通过解码器对中间编码进行解码得到输出序列。

Figure 1 为Encoder-Decoder结构示意图,Encoder框中是一个正常的Rnn结构,输入序列 ( x 1 , x 2 , . . . , x T ) (x1,x2,...,xT) (x1,x2,...,xT),输出 C C C。 C C C是上文中说到的中间序列。Decoder框中同样为Rnn结构, 其输入是中间编码 C C C, 输出为输出序列 ( y 1 , y 2 , . . . , y T ) (y1,y2,...,yT) (y1,y2,...,yT)。
这里Decoder部分的Rnn和Encoder部分的Rnn稍有不同。
Encoder的Rnn为正常使用,由上一时刻隐状态 h t − 1 h_{t-1} ht−1和该时刻输入 x t x_{t} xt进行隐状态更新,公式为:
h t = f ( h t − 1 , x t ) h_{t} = f(h_{t-1}, x_{t}) ht=f(ht−1,xt)
Decoder的Rnn在 t t t 时刻的输出由 t t t 时刻的隐藏状态 s t s_{t} st、 t − 1 t-1 t−1时刻的输出 y t − 1 y_{t-1} yt−1和 C C C 计算得出,公式为:
P ( y t ∣ y t − 1 , y t − 2 , . . . , y 1 , C ) = g ( s t , y t − 1 , C ) P(y_{t}| y_{t-1}, y_{t-2}, ..., y_{1}, C) = g(s_{t}, y_{t-1}, C) P(yt∣yt−1,yt−2,...,y1,C)=g(st,yt−1,C)
Encoder和Decoder的训练目标是最大化条件概率分布:
m a x θ 1 N ∑ n = 1 N l o g P θ ( y n ∣ x n ) max_{\theta} \frac{1}{N} \displaystyle\sum_{n=1}^N logP_{\theta}(y_{n}|x_{n}) maxθN1n=1∑NlogPθ(yn∣xn)
模型参数为 θ θ θ,出现 x n x_{n} xn时 y n y_{n} yn的条件概率是 P ( y n ∣ x n ) P(y_{n}|x_{n}) P(yn∣xn), l o g P logP logP是单调递增的,更容易计算,将 N 个 P N个P N个P加起来求平均,就是最终的优化目标,输出序列输出几个符号, N N N就是几
这里不懂的可以看博客:语言模型:马尔可夫模型
2. Attention
Seq2Seq中Encoder通过 C C C 将信息传给Decoder, C C C承载的是训练数据中序列的信息,而 C C C仅仅是Rnn隐藏序列的最后一个,表达的是整个序列的信息。而如果想要更好的结果,将Encoder序列的所有隐藏状态都给Decoder显然更好,因此 C C C 可以是Encoder所有时刻的隐藏状态之和,此时的 C C C 表示Encoder 中又包含了各个词的隐藏信息;当然,在解码时生成某一个词有时候并不需要依赖输入序列所有的词的信息,此时,只要给Encoder每个时刻隐藏状态一个权值,再相加,就可以得到生成指定词最适合的编码信息了,换种说法就是当生成某个词的时候我们的注意力只放在那些对它有用的词信息上。这就是注意力机制的逻辑。
2.1 Bahdanau Attention Mechanism
先来介绍Bahdanau在2015年提出的attention mechanism。
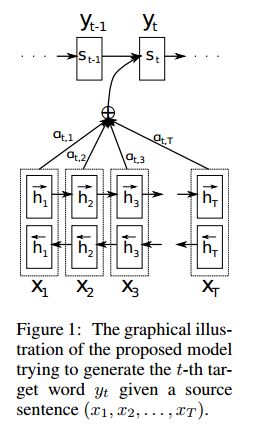
同样,Decoder通过计算条件概率分布的方式来预测输出:
P ( y i ∣ y i − 1 , y i − 2 , . . . , y 1 , X ) = g ( s i , y i − 1 , c i ) P(y_{i}| y_{i-1}, y_{i-2}, ..., y_{1}, X) = g(s_{i}, y_{i-1}, c_{i}) P(yi∣yi−1,yi−2,...,y1,X)=g(si,yi−1,ci)
注意:Encoder-Decoder中的 C C C 是固定不变得信息,而这里 c i c_{i} ci 是一个变化信息,称为第 i i i 个输出词的对应的输入上下文向量,同样代表输入句子的表征,不同时刻注意力集中在不同的词上面。
状态 s i s_{i} si 是 i i i 时刻Decoder Rnn的隐藏状态:
s i = f ( s i − 1 , y i − 1 , c i ) s_{i} = f(s_{i-1}, y_{i-1}, c_{i}) si=f(si−1,yi−1,ci)
上下文向量 c i c_{i} ci 由输入序列的隐藏层状态 h 1 , . . . , h T h_{1},...,h_{T} h1,...,hT产生。每个 h i h_{i} hi包含整个序列的信息的同时更多的关注第 i i i 个词的上下文信息。 c i c_{i} ci 的计算:
c i = ∑ j = 1 T α i j h j c_{i} = \displaystyle\sum_{j=1}^T \alpha_{ij}h_{j} ci=j=1∑Tαijhj
这里的 α i j \alpha_{ij} αij 是每个 h j h_{j} hj 的权重得分,范围为(0,1):
α i j = e x p ( e i j ) ∑ k = 1 T e x p ( e i k ) \alpha_{ij} = \frac{exp(e_{ij})}{\displaystyle\sum_{k=1}^T exp(e_{ik})} αij=k=1∑Texp(eik)exp(eij)
e i j = a ( s i − 1 , h j ) e_{ij} = a(s_{i-1}, h_{j}) eij=a(si−1,hj)
e i j e_{ij} eij 为Decoder ( i − 1 ) (i−1) (i−1) 位置的隐藏状态 s i − 1 s_{i-1} si−1和Encoder中 j j j 位置的隐藏状态 h j h_{j} hj经过计算方式 a a a 得到的分值。
a a a的计算方式为:
a = v a T t a n h ( W a s i − 1 + U a h j ) a = v_a^T tanh(W_{a}s_{i-1}+U_{a}h_{j}) a=vaTtanh(Wasi−1+Uahj)
这里的 W a 和 U a W_a和U_{a} Wa和Ua为参数矩阵,作为可训练参数加入整个网络,所以attention也相当于是一层网络, W a 和 U a W_a和U_{a} Wa和Ua是这层网络的参数,所以attention的参数矩阵也是可以训练得到的。
网络经过训练可以学习到:解码器在输出一个序列元素时,哪些编码器信息更有价值,更值得被关注,这就是注意力机制的通俗解释。
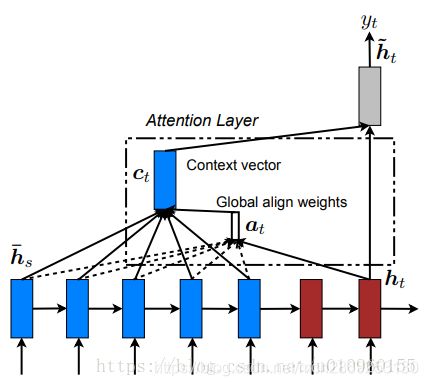
2.2 Luong Attention Mechanism
Luong 在论文4中提出一种 a a a(对齐函数) 的新计算方式,
a = v a T t a n h ( W a s i + U a h j ) a = v_a^T tanh(W_{a}s_{i}+U_{a}h_{j}) a=vaTtanh(Wasi+Uahj)
需要注意的是在Luong提出的Attention Mechanism中,是通过Decoder i i i 时刻的隐藏层状态 s i s_{i} si 和encoder的隐藏层状态 h j h_{j} hj 来确定 a a a的值,而在Bahdanau中是通过Decoder ( i − 1 ) (i−1) (i−1) 时刻的隐藏状态 s i − 1 s_{i-1} si−1和Encoder中 j j j 位置的隐藏状态 h j h_{j} hj经过计算。
转载自:https://blog.csdn.net/ilikede/article/details/81035889#commentBox