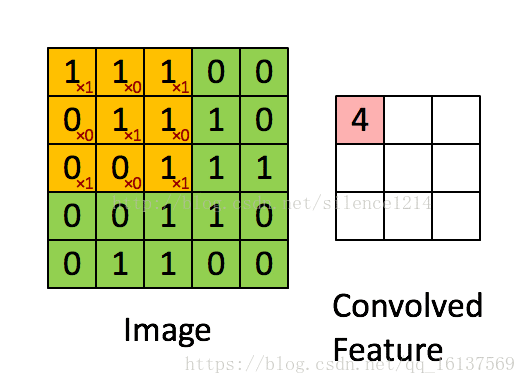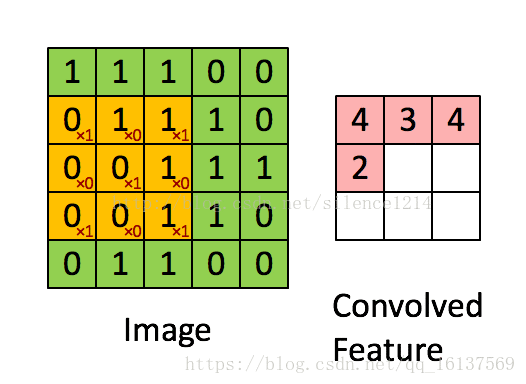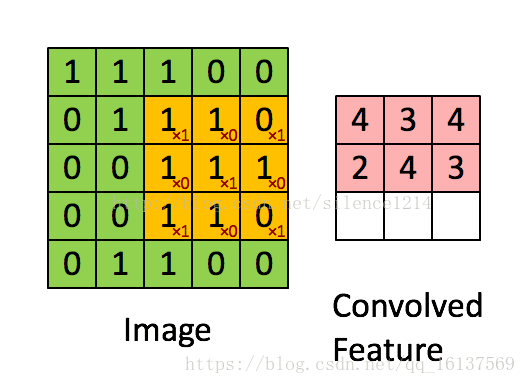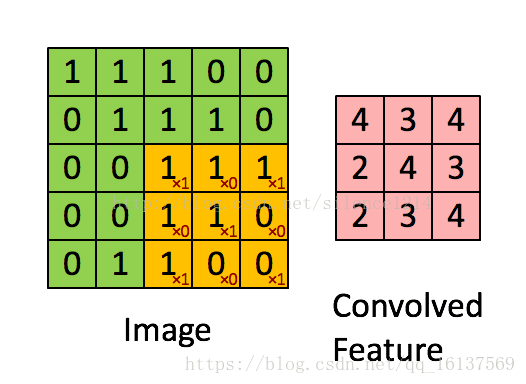
回顾
上一篇博客《详解神经网络的前向传播和反向传播》推导了普通神经网络(多层感知器)的反向传播过程,这篇博客参考刘建平Pinard 《卷积神经网络(CNN)反向传播算法》对卷积神经网络中反向传播的不同之处进行了讨论。
我们先简单回顾一下普通神经网络(DNN)中反向传播的四个核心公式:
δLj=∂C∂zLj=∂C∂aLj∂aLj∂zLj=∂C∂aLjσ′(zLj)(BP1) (BP1) δ j L = ∂ C ∂ z j L = ∂ C ∂ a j L ∂ a j L ∂ z j L = ∂ C ∂ a j L σ ′ ( z j L )
δl=((wl+1)Tδl+1)⊙σ′(zl)(BP2) (BP2) δ l = ( ( w l + 1 ) T δ l + 1 ) ⊙ σ ′ ( z l )
∂C∂blj=∂C∂zlj∂zlj∂blj=∂C∂zlj=δlj(BP3) (BP3) ∂ C ∂ b j l = ∂ C ∂ z j l ∂ z j l ∂ b j l = ∂ C ∂ z j l = δ j l
∂C∂wljk=∂C∂zlj∂zLj∂wljk=∂C∂zljal−1k=al−1kδlj(BP4) (BP4) ∂ C ∂ w j k l = ∂ C ∂ z j l ∂ z j L ∂ w j k l = ∂ C ∂ z j l a k l − 1 = a k l − 1 δ j l
只要计算出
∂C∂wljk ∂ C ∂ w j k l 和
∂C∂blj ∂ C ∂ b j l 就能使用梯度下降算法对网络进行训练了。
问题提出
那么我们能不能直接在CNN上直接套用DNN的传播算法呢?当然不能,不然我也不会写这篇博客了嘿嘿。我们先从最直观的网络结构的角度来分析一下。
1. 全连接层
CNN中的全连接层和DNN层结构完全一致,这个可以照搬。
2. 池化层
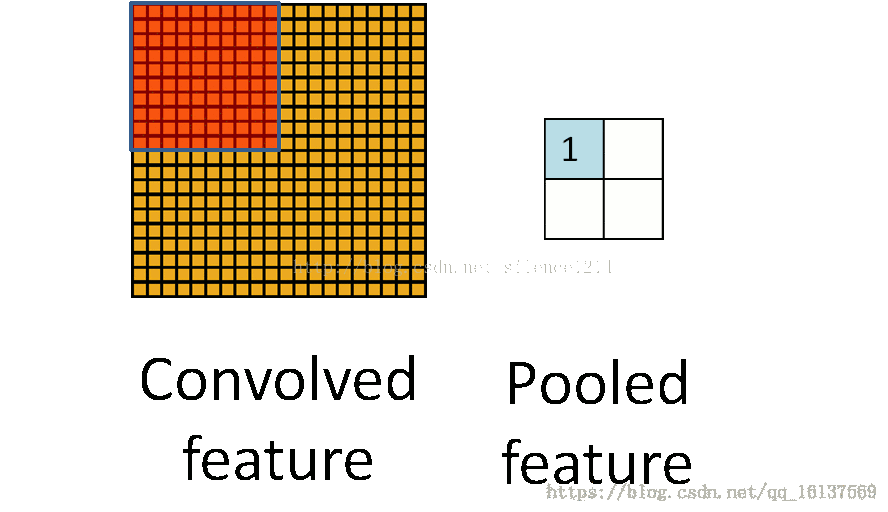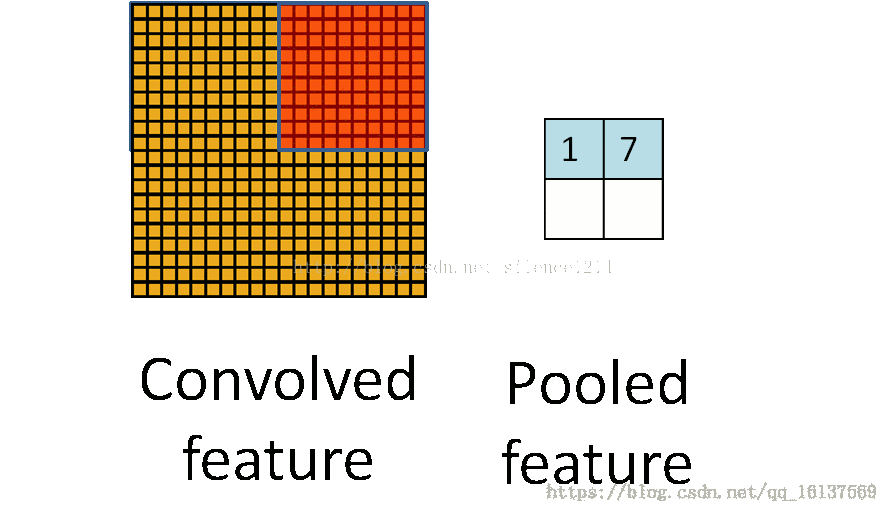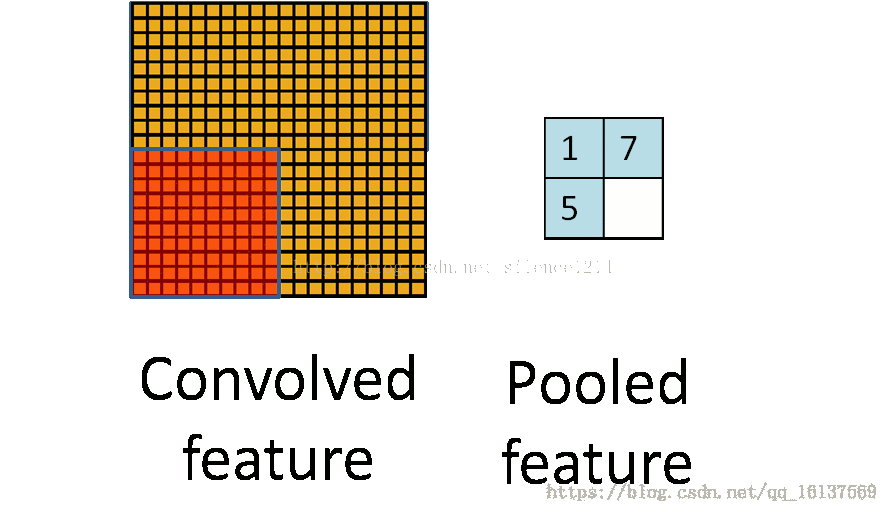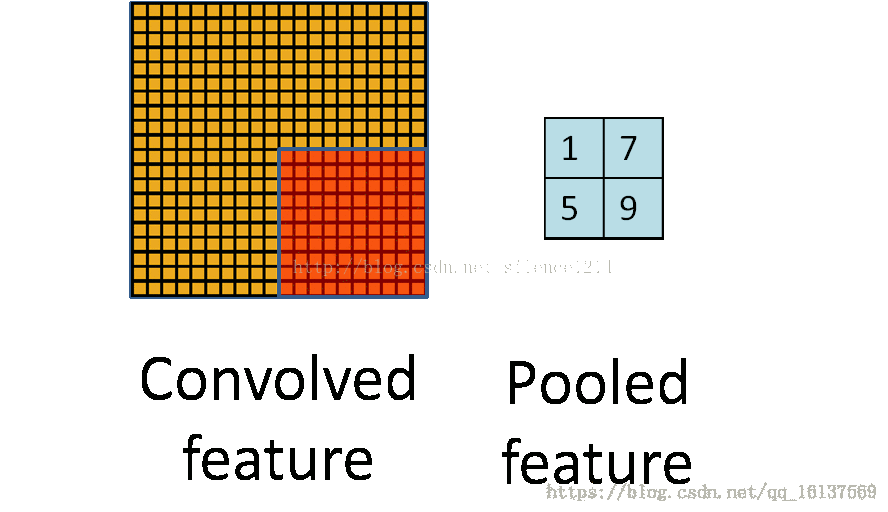
池化层简而言之就是利用feature map的统计特征来代表这块区域。如下图所示,可以利用红色区域的均值、最大值、最小值等统计量来代表该块红色区域,一方面引入了平移不变性(这个在另外一篇博客中讲),一方面减少了参数数量。但是我们在反向传播时,知道右边 2×2 2 × 2 区域的 δl δ l 的情况下,如何计算左边完整区域的 δl−1 δ l − 1 ?而且池化层一般没有激活函数,这个问题怎么处理?
3. 卷积层
卷积层是通过张量卷积,或者说是若干个矩阵卷积求和而得到当前层的输出,这和DNN直接进行矩阵乘法有很大区别,那么如何递推相应的
δl−1 δ l − 1 呢?
4. 反卷积层和BN层
这个日后弄懂再补上来。
池化层的反向传播
池化层没有激活函数可以直接看成用线性激活函数,即 σ(z)=z σ ( z ) = z ,所以 σ′(z)=1 σ ′ ( z ) = 1 。接下来看看池化层如何递推 δl δ l 。
在前向传播时,我们一般使用max或average对输入进行池化,而且池化区域大小已知。反向传播就是要从缩小后的误差 δl+1 δ l + 1 ,还原池化前较大区域对应的误差 δl δ l 。根据(BP2), δl=((wl+1)Tδl+1)⊙σ′(zl) δ l = ( ( w l + 1 ) T δ l + 1 ) ⊙ σ ′ ( z l ) ,在DNN中 wl+1 w l + 1 是已知的,所以我们可以直接通过矩阵乘法将 l+1 l + 1 层的误差映射回 l l 层的误差,但对于池化层,要求 (wl+1)Tδl+1 ( w l + 1 ) T δ l + 1 就需要一些特殊的操作了。
用一个例子可以很清楚的解释这一过程:假设现在我们是步长为1的 2×2 2 × 2 池化, 4×4 4 × 4 大小的区域经过池化后变为 2×2 2 × 2 。如果 δl δ l 的第k个子矩阵为:
δl+1k=[2486] δ k l + 1 = [ 2 8 4 6 ]
首先我们要确定
δl+1k δ k l + 1 中4个误差值分别和原来
4×4 4 × 4 大小的哪个子区域所对应,根据前向传播中池化窗口的移动过程,我们可以很轻松的确定2对应左上角
2×2 2 × 2 的区域,8对应右上角
2×2 2 × 2 的区域,以此类推。这一步完成之后,我们就要对不同类型的池化进行不同的操作。
如果是max pooling,我们只需要记录前向传播中最大值的位置,然后将误差放回去即可。如果最大值位置分别为
2×2 2 × 2 的左上,右下,右上,左下,还原后的矩阵为:
(wl+1)Tδl+1=⎡⎣⎢⎢⎢2000004000060800⎤⎦⎥⎥⎥ ( w l + 1 ) T δ l + 1 = [ 2 0 0 0 0 0 0 8 0 4 0 0 0 0 6 0 ]
如果是average pooing,我们只需要将池化单元的误差平均值放回原来的子矩阵即可:
(wl+1)Tδl+1=⎡⎣⎢⎢⎢0.50.5110.50.511221.51.5221.51.5⎤⎦⎥⎥⎥ ( w l + 1 ) T δ l + 1 = [ 0.5 0.5 2 2 0.5 0.5 2 2 1 1 1.5 1.5 1 1 1.5 1.5 ]
可以发现这其实就是将上一层的误差进行一次池化的逆操作,还是比较容易理解的。
得到了
(wl+1)Tδl+1 ( w l + 1 ) T δ l + 1 之后就可以利用
δl=((wl+1)Tδl+1)⊙σ′(zl) δ l = ( ( w l + 1 ) T δ l + 1 ) ⊙ σ ′ ( z l ) 求得
δlk δ k l 了。
卷积层的反向传播
继续回到方程(BP2), δl=((wl+1)Tδl+1)⊙σ′(zl) δ l = ( ( w l + 1 ) T δ l + 1 ) ⊙ σ ′ ( z l ) ,那你可能会问,之前说池化层因为 wl+1 w l + 1 无法直接计算,所以需要特殊操作,那么卷积核的参数不是知道吗,岂不是可以直接代入计算了。是带进去计算没错,但是权重矩阵需要旋转180°。为什么呢,下面以一个简单的例子说明。
假设 l l 层的激活输出是一个 3×3 3 × 3 的矩阵,第 l+1 l + 1 层卷积核 Wl+1 W l + 1 是一个 2×2 2 × 2 的矩阵,卷积步长为1,则输出 zl+1 z l + 1 是一个 2×2 2 × 2 的矩阵。我们简化 bl=0 b l = 0 ,则有:
zl+1=al∗Wl+1(1) (1) z l + 1 = a l ∗ W l + 1
列出
a a ,
W W ,
z z 的矩阵表达式如下:
[z11z21z12z22]=⎡⎣⎢a11a21a31a12a22a32a13a23a33⎤⎦⎥∗[w11w21w12w22](2) (2) [ z 11 z 12 z 21 z 22 ] = [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] ∗ [ w 11 w 12 w 21 w 22 ]
利用卷积的定义,很容易得出:
z11=a11w11+a12w12+a21w21+a22w22z12=a12w11+a13w12+a22w21+a23w22z21=a21w11+a22w12+a31w21+a32w22z22=a22w11+a23w12+a32w21+a33w22(3) (3) z 11 = a 11 w 11 + a 12 w 12 + a 21 w 21 + a 22 w 22 z 12 = a 12 w 11 + a 13 w 12 + a 22 w 21 + a 23 w 22 z 21 = a 21 w 11 + a 22 w 12 + a 31 w 21 + a 32 w 22 z 22 = a 22 w 11 + a 23 w 12 + a 32 w 21 + a 33 w 22
接下来我们计算
∂C∂al ∂ C ∂ a l :
∇al=∂C∂al=∂C∂zl+1∂zl+1∂al=δl+1∂zl+1∂al(4) (4) ∇ a l = ∂ C ∂ a l = ∂ C ∂ z l + 1 ∂ z l + 1 ∂ a l = δ l + 1 ∂ z l + 1 ∂ a l
由方程(2)可以得知,
∂zl+1∂al ∂ z l + 1 ∂ a l 和
Wl+1 W l + 1 相关。假设
δl+1=[δ11δ21δ12δ22] δ l + 1 = [ δ 11 δ 12 δ 21 δ 22 ]
在式(3)的4个等式中,
a11 a 11 只和
z11 z 11 有关(
z12,z21,z22 z 12 , z 21 , z 22 表达式中均没有
a11 a 11 ),所以
∇a11=δl+111∂zl+111∂al11+δl+112∂zl+112∂al11+δl+121∂zl+121∂al11+δl+122∂zl+122∂al11=δ11w11 ∇ a 11 = δ 11 l + 1 ∂ z 11 l + 1 ∂ a 11 l + δ 12 l + 1 ∂ z 12 l + 1 ∂ a 11 l + δ 21 l + 1 ∂ z 21 l + 1 ∂ a 11 l + δ 22 l + 1 ∂ z 22 l + 1 ∂ a 11 l = δ 11 w 11
同理可以得到其他8个
∇a ∇ a :
∇a12=δ11w12+δ12w11∇a13=δ12w12∇a21=δ11w21+δ21w11∇a22=δ11w22+δ12w21+δ21w12+δ22w11∇a23=δ12w22+δ22w12∇a31=δ21w21∇a32=δ21w22+δ22w21∇a33=δ22w22 ∇ a 12 = δ 11 w 12 + δ 12 w 11 ∇ a 13 = δ 12 w 12 ∇ a 21 = δ 11 w 21 + δ 21 w 11 ∇ a 22 = δ 11 w 22 + δ 12 w 21 + δ 21 w 12 + δ 22 w 11 ∇ a 23 = δ 12 w 22 + δ 22 w 12 ∇ a 31 = δ 21 w 21 ∇ a 32 = δ 21 w 22 + δ 22 w 21 ∇ a 33 = δ 22 w 22
其实上面的9个式子可以用一个矩阵卷积的形式统一表示:
⎡⎣⎢∇a11∇a21∇a31∇a12∇a22∇a32∇a13∇a23∇a33⎤⎦⎥=⎡⎣⎢⎢⎢00000δ11δ2100δ12δ2200000⎤⎦⎥⎥⎥∗[w22w12w21w11](5) (5) [ ∇ a 11 ∇ a 12 ∇ a 13 ∇ a 21 ∇ a 22 ∇ a 23 ∇ a 31 ∇ a 32 ∇ a 33 ] = [ 0 0 0 0 0 δ 11 δ 12 0 0 δ 21 δ 22 0 0 0 0 0 ] ∗ [ w 22 w 21 w 12 w 11 ]
为了符合梯度计算,我们在误差矩阵周围填充了一圈0,此时我们将卷积核翻转后和反向传播的梯度误差进行卷积,就得到了前一次的梯度误差,然后用(BP2)就可以得到上一层的误差。卷积层的(BP2)形式如下:
δl=(δl+1∗rot180(wl+1))⊙σ′(zl) δ l = ( δ l + 1 ∗ r o t 180 ( w l + 1 ) ) ⊙ σ ′ ( z l )
还需要注意的是,在利用(BP4)推导该层权重的梯度
∂C∂wl ∂ C ∂ w l 时,也需要进行一个旋转180°的操作:
∂C∂wl=∂C∂zl∂zL∂wl=δl∂zL∂wl=δl∗rot180(al−1) ∂ C ∂ w l = ∂ C ∂ z l ∂ z L ∂ w l = δ l ∂ z L ∂ w l = δ l ∗ r o t 180 ( a l − 1 )
对于偏置
b b 则有些特殊,因为
δl δ l 是3维张量,而
bl b l 只是一个一维向量,不能像DNN中那样直接
∂C∂bl=δl ∂ C ∂ b l = δ l ,通常是将
δl δ l 的各个子矩阵分别求和,得到一个误差向量,即
bl b l 的梯度:
∂C∂bl=∑u,v(δl)u,v ∂ C ∂ b l = ∑ u , v ( δ l ) u , v
总结
虽然CNN的反向传播和DNN有所不同,但本质上还是4个核心公式的变形,思路是一样的。