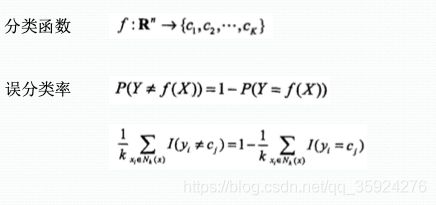《统计学习方法》 第三章 k近邻法总结及代码实现
本文总结内容参考于李航老师的《统计学习方法》及其配套课件
原文代码作者:https://github.com/wzyonggege/statistical-learning-method
k近邻法的输入为实例的特征向量,对应于特征空间的点;输出为实例 的类别,可以取多类。k近邻法假设给定一个训练数据集,其中的实例类别已定。分类 时,对新的实例,根据其k个最近邻的训练实例的类别,通过多数表决等方式进行预测。 因此,k近邻法不具有显式的学习过程。k近邻法实际上利用训练数据集对特征向量空间进 行划分,并作为其分类的“模型”。
KNN算法的一般流程——
收集数据:可以使用任何方法
准备数据:距离计算所需要的数值,最后是结构化的数 据格式。
分析数据:可以使用任何方法
训练算法: (此步骤kNN)中不适用
测试算法:计算错误率
使用算法:首先需要输入样本数据和结构化的输出结果, 然后运行k-近邻算法判定输入数据分别属于哪个分类, 最后应用对计算出的分类执行后续的处理。
- 模型
特征空间中,对每个训练实例点ix,距离该点比其他点更近的所有点组成一个区域, 叫作单元(cell)。每个训练实例点拥有一个单元,所有训练实例点的单元构成对特征空 间的一个划分。最近邻法将实例ix的类iy作为其单元中所有点的类标记(class label)。这 样,每个单元的实例点的类别是确定的。
- 距离度量
- K值的选择
如果选择较小的K值:“学 习”的近似误差(approximation error)会减小,但 “学习”的估计误差(estimation error) 会增大;噪声敏感 ;K值的减小就意味着整体模型变得复杂,容易发生过拟合.
如果选择较大的K值, 减少学习的估计误差,但缺点是学习的近似误差会增大. K值的增大 就意味着整体的模型变得简单.
- 分类决策规则
代码在jupyter notebook中运行
import math
from itertools import combinations
'''
p = 1 曼哈顿距离
p = 2 欧氏距离
p = inf 闵式距离minkowski_distance
'''
#度量距离
def L(x, y, p =2):
if len(x) == len(y) and len(x) >1 :
sum = 0
for i in range(len(x)):
sum += math.pow(abs(x[i] - y[i]), p)
return math.pow(sum, 1/p)
else:
return 0
x1 = [1, 1]
x2 = [5, 1]
x3 = [4, 4]
for i in range(1, 5):
#format格式化函数,通过 {} 和 : 来代替以前的 %
#此时r为一个字典,keys为点与点,values为度量距离
r = { '1-{}'.format(c):L(x1, c, p= i) for c in [x2, x3]}
#zip()将对象中的对应元素打包成一个个元组
print(min(zip(r.values(), r.keys())))输出结果为:
(4.0, '1-[5, 1]')
(4.0, '1-[5, 1]')
(3.7797631496846193, '1-[4, 4]')
(3.5676213450081633, '1-[4, 4]')
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from collections import Counter
iris = load_iris()
#矩阵数据表,将列名设为iris的特征
df = pd.DataFrame(iris.data,columns = iris.feature_names)
#加入一列为分类标签
df['label'] = iris.target
#重命名列名(需要将每个都列出)
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
df得到150条数据
#将标签为0、1的两种花,根据特征为长度和宽度打点表示
plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
#按行索引,取出第0列第1列和最后一列,即取出sepal长度、宽度和标签
data = np.array(df.iloc[:100, [0, 1, -1]])
##X为sepal length,sepal width y为标签
X, y = data[:,:-1], data[:,-1]
# train_test_split函数用于将矩阵随机划分为训练子集和测试子集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
class KNN:
def __init__(self, X_train, y_train, n_neighbors=3, p=2):
"""
parameter: n_neighbors 临近点个数
parameter: p 距离度量
"""
self.n = n_neighbors
self.p = p
self.X_train = X_train
self.y_train = y_train
def predict(self, X):
# 取出n个点,放入空的列表,列表中存放预测点与训练集点的距离及其对应标签
knn_list = []
for i in range(self.n):
#np.linalg.norm 求范数
dist = np.linalg.norm(X - self.X_train[i], ord=self.p)
knn_list.append((dist, self.y_train[i]))
#再取出训练集剩下的点,然后与n_neighbor个点比较大叫,将距离大的点更新
#保证knn_list列表中的点是距离最小的点
for i in range(self.n, len(self.X_train)):
'''此处 max(num,key=lambda x: x[0])用法:
x:x[]字母可以随意修改,求最大值方式按照中括号[]里面的维度,
[0]按照第一维,
[1]按照第二维
'''
max_index = knn_list.index(max(knn_list, key=lambda x: x[0]))
dist = np.linalg.norm(X - self.X_train[i], ord=self.p)
#g更新最近邻中距离比当前点远的点
if knn_list[max_index][0] > dist:
knn_list[max_index] = (dist, self.y_train[i])
# 统计分类最多的点,确定预测数据的分类
knn = [k[-1] for k in knn_list]
#counter为计数器,按照标签计数
count_pairs = Counter(knn)
#排序
max_count = sorted(count_pairs, key=lambda x:x)[-1]
return max_count
#预测的正确率
def score(self, X_test, y_test):
right_count = 0
n = 10
for X, y in zip(X_test, y_test):
label = self.predict(X)
if label == y:
right_count += 1
return right_count / len(X_test)clf = KNN(X_train, y_train)
clf.score(X_test, y_test)
#预测点
test_point = [6.0, 3.0]
#预测结果
print('Test Point: {}'.format(clf.predict(test_point)))
plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')
#打印预测点
plt.plot(test_point[0], test_point[1], 'bo', label='test_point')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()得到:Test Point: 1.0
可以从图中看到预测点明显分类正确
print(clf.score(X_test, y_test))
#结果为1.0