【亮亮笔记】——动态规划的0/1背包问题之穷举法求解
小编这二天接触到了动态规划,学习动态规划当然少不了动态规划的经典问题-0/1背包问题了,在网上也是找了好多篇介绍动态规划的博客,我始终不能理解其中的一些代码,而我自己研究的话呢就一直没有出别人的代码思路中走出来,这不昨天刚走出来,今天我就抽时间来写这篇博客,以便日后翻阅。
问题描述:
假设现有容量m kg的背包,另外有i个物品,重量分别为w[1] w[2] ... w[i] (kg),价值分别为p[1] p[2] ... p[i] (元),将哪些物品放入背包可以使得背包的总价值最大?最大价值是多少?
(示例一:m=10 i=3 重量和价值分别为 3kg-4元 4kg-5元 5kg-6元 )
分析:
先不考虑背包能否放下多少物品,每个物品只有不放入背包和放入背包这二种可能,一共有 i 件物品,所以一共有 2 的 i 次方种可能,设不放入背包为 0 ,放入背包为 1,那么就有下面的场景(小编是个没有艺术细胞的汉子,如果辣眼睛的话,请自带墨镜,如亮瞎眼,本人概不负责)
那么就变成了对 i 个数字进行组合的数学问题(这也是为什么叫0/1背包问题的原因),我们都知道二进制,也就是对 i 位二进制数进行组合,那么组合中为 1 的那一位就是被放入背包中的物品,通过位数就能得到这个物品的重量和价值,统计这一个组合的总重量与总价值并与其它组合进行比较,不超过背包容量,能放入背包的物品的最大总价值
相信大家看到这,思路也差不多有头绪了,下面上我自己的代码,帮助大家进一步理解:
代码展示:
using System;
namespace _009_背包问题_穷举法
{
internal class Program
{
private static void Main(string[] args)
{
int[] w = {0, 3, 4, 5}; //物品重量
int[] P = {0, 4, 5, 6}; //物品价格
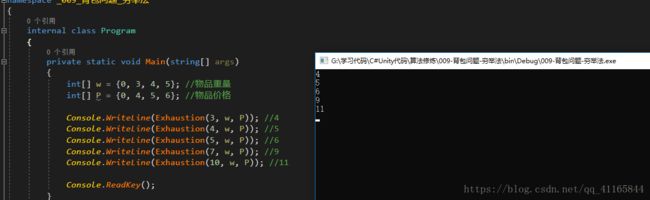
Console.WriteLine(Exhaustion(3, w, P)); //4
Console.WriteLine(Exhaustion(4, w, P)); //5
Console.WriteLine(Exhaustion(5, w, P)); //6
Console.WriteLine(Exhaustion(7, w, P)); //9
Console.WriteLine(Exhaustion(10, w, P)); //11
Console.ReadKey();
}
///
/// 穷举法
///
///
///
///
public static int Exhaustion(int m, int[] w, int[] p)
{
var i = w.Length - 1; //一共多少个物品
var MaxPrice = 0; //背包的最大价值
var Maxweigth = 0; //背包的最重量
for (var j = 0; j < Math.Pow(2, i); j++) //
{
//已经计算出 i 个物品一共有多少种放入背包的方案
var weightTotal = 0; //方案中放入背包的物品的总重量
var priceTotal = 0; //方案中背包中物品的总价值
for (var number = 1; number <= i; number++)
{
var result = Get2(j, number); //得到该物品是否放入了背包中
if (result)
{
//物品放入到背包中后,加上该物品的重量与价值
weightTotal += w[number];
priceTotal += p[number];
}
}
if (priceTotal > MaxPrice && m >= weightTotal) MaxPrice = priceTotal;//得到目前的最佳的方案
}
return MaxPrice;
}
///
/// 得到哪个物品放入了背包
///
/// 放入背包的方案
///
/// 运行结果截图:
另外提供一个关于动态规划的其他问题的链接,以供加深理解漫画:什么是动态规划?(整合版)