条件随机场
条件随机场
- 概率无向图模型
- 条件随机场的定义与形式
- 条件随机场的参数化形式
条件随机场是给定一组输入随机变量下另一组输出随机变量的条件概率分布模型,其特点是假设输出随机变量构成马尔可夫随机场。条件随机场可以用于不同的预测问题,本书仅讨论它在标注问题的应用。因此主要讲述线性链条件随机场,这时,问题变成了由输入序列对输出序列预测判别模型,形式为对数线性模型,其学习方法通常是极大似然估计或正则化的极大似然估计。首先叙述条件随机场的 定义和各种表示方法,最后介绍条件随机场的3个基本问题: 概率计算、 学习问题和 预测问题。
概率无向图模型
图的概念:图是由结点( v v v)及连接结点的边( e e e)组成的集合。结点和边的集合分别记作 V V V和 E E E,图记作 G = ( V , E ) G=(V,E) G=(V,E)。无向图是指边没有方向的图。
概率图模型是由图表示的概率分布。设有联合概率分布 P ( Y ) P(Y) P(Y), Y ∈ y Y \in y Y∈y是一组随机变量。由无向图 G = ( V , E ) G=(V,E) G=(V,E)表示概率分布 P ( Y ) P(Y) P(Y),即在图 G G G中,结点 v ∈ V v \in V v∈V表示一个随机变量 Y v , Y = ( Y v ) v ∈ V Y_v,Y=(Y_v) v \in V Yv,Y=(Yv)v∈V;边 e ∈ E e \in E e∈E表示随机变量之间的概率依赖关系。
给定一个联合概率分布 P ( Y ) P(Y) P(Y)和表示它的无向图 G G G。首先定义无向图表示的随机变量之间存在的成对马尔可夫性、局部马尔可夫性和全局马尔可夫性。这三个性质是等价的。
成对马尔可夫性:设 u u u和 v v v是无向图 G G G中任意两个没有边连接的结点,结点 u u u和 v v v分别对应随机变量 Y u Y_u Yu和 Y v Y_v Yv。其他所有结点为 O O O,对应的随机变量组是 Y O Y_O YO。成对马尔可夫性是指给定随机变量组 Y O Y_O YO的条件下随机变量 Y u Y_u Yu和 Y v Y_v Yv是条件独立的,即 P ( Y u , Y v ∣ Y O ) = P ( Y u ∣ Y O ) P ( Y v ∣ Y O ) P(Y_u,Y_v|Y_O)=P(Y_u|Y_O)P(Y_v|Y_O) P(Yu,Yv∣YO)=P(Yu∣YO)P(Yv∣YO)
概率无向图模型:设有联合概率分布 P ( Y ) P(Y) P(Y),由无向图 G = ( V , E ) G=(V,E) G=(V,E)表示,在图 G G G中,结点表示随机变量,边表示随机变量之间的依赖关系。如果联合概率分布 P ( Y ) P(Y) P(Y)满足成对、局部和全局马尔可夫性,就称此联合概率分布为概率无向图模型,或马尔可夫随机场。
给定概率无向图模型,设其无向图为 G G G, C C C为 G G G上的最大团, Y C Y_C YC表示 C C C对应的随机变量。那么概率无向图模型的联合概率分布 P ( Y ) P(Y) P(Y)可写作图中所有最大团 C C C上的函数 Ψ C ( Y C ) \Psi_C(Y_C) ΨC(YC)的乘积形式,即 P ( Y ) = 1 Z ∏ C Ψ C ( Y C ) P(Y)=\frac{1}{Z}\prod_C\Psi_C(Y_C) P(Y)=Z1C∏ΨC(YC)其中, Z Z Z是规范化因子,由式 Z = ∑ γ ∏ C Ψ C ( Y C ) Z=\sum_{\gamma}\prod_C\Psi_C(Y_C) Z=γ∑C∏ΨC(YC)规范化因子保证 P ( Y ) P(Y) P(Y)构成一个概率分布。函数 Ψ C ( Y C ) \Psi_C(Y_C) ΨC(YC)称为势函数。这里要求势函数 Ψ C ( Y C ) \Psi_C(Y_C) ΨC(YC)是严格正的,通常定义为指数函数; Ψ C ( Y C ) = exp { − E ( Y C ) } \Psi_C(Y_C)=\exp\{-E(Y_C)\} ΨC(YC)=exp{−E(YC)}
条件随机场的定义与形式
设 X X X与 Y Y Y是随机变量, P ( Y ∣ X ) P(Y|X) P(Y∣X)是在给定 X X X的条件下 Y Y Y的条件随机分布。若随机变量 Y Y Y构成一个由无向图 G = ( V , E ) G=(V,E) G=(V,E)表示的马尔可夫随机场,即 P ( Y v ∣ X , Y w , w ≠ v ) = P ( Y v ∣ X , Y w , w v ) P(Y_v|X,Y_w,w \neq v)=P(Y_v|X,Y_w,w~v) P(Yv∣X,Yw,w=v)=P(Yv∣X,Yw,w v)对任意结点 v v v成立,则称条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)为条件随机场。式中 w v w~v w v表示在图 G = ( V , E ) G=(V,E) G=(V,E)中与结点 v v v有边连接的所有结点 w w w, w ≠ v w \neq v w=v表示结点 v v v以外的所有结点, Y v Y_v Yv, Y u Y_u Yu与 Y w Y_w Yw为结点 v v v, u u u与 w w w对应的随机变量。
以下主要讨论线性链的情况
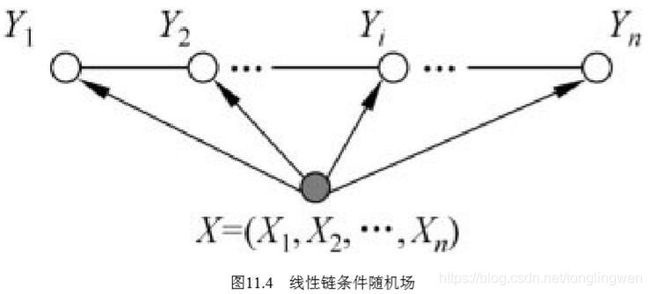
线性条件随机场:设 X = ( X 1 , X 2 , . . . , X n ) X=(X_1,X_2,...,X_n) X=(X1,X2,...,Xn), Y = ( Y 1 , Y 2 , . . . , Y n ) Y=(Y_1,Y_2,...,Y_n) Y=(Y1,Y2,...,Yn)均为线性链表示的随机变量序列,若在给定随机变量序列 X X X的条件下,随机变量序列 Y Y Y的条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)构成条件随机场,即满足马尔可夫性 P ( Y i ∣ X , Y 1 , . . . , Y i − 1 , Y i + 1 , . . . , Y n ) = P ( Y i ∣ X , Y i − 1 , Y i + 1 ) P(Y_i|X,Y_1,...,Y_{i-1},Y_{i+1},...,Y_n)=P(Y_i|X,Y_{i-1},Y_{i+1}) P(Yi∣X,Y1,...,Yi−1,Yi+1,...,Yn)=P(Yi∣X,Yi−1,Yi+1) i = 1 , 2 , . . . , n ( 在 i = 1 和 n 时 只 考 虑 单 边 ) i=1,2,...,n \quad (在i=1和n时只考虑单边) i=1,2,...,n(在i=1和n时只考虑单边)则称 P ( Y ∣ X ) P(Y|X) P(Y∣X)为线性链条件随机场。在标注问题中, X X X表示输入观测序列, Y Y Y表示对应的输出标记序列或状态序列。
条件随机场的参数化形式
设 P ( Y ∣ X ) P(Y|X) P(Y∣X)为线性链条件随机场,则在随机变量 X X X取值为 x x x的条件下,随机变量 Y Y Y取值为 y y y的条件概率具有如下形式: P ( y ∣ x ) = 1 Z ( x ) exp ( ∑ i , k λ k t k ( y i − 1 , y i , x , i ) + ∑ i , l μ l s l ( y i , x , i ) ) P(y|x)=\frac{1}{Z(x)}\exp(\sum_{i,k}\lambda_kt_k(y_{i-1},y_i,x,i)+\sum_{i,l}\mu_ls_l(y_i,x,i)) P(y∣x)=Z(x)1exp(i,k∑λktk(yi−1,yi,x,i)+i,l∑μlsl(yi,x,i))式中, t k t_k tk和 s l s_l sl是特征函数, λ k \lambda_k λk和 μ l \mu_l μl是对应的权重。 Z ( x ) Z(x) Z(x)是规范化因子,求和是在所有可能的输出序列上进行的。